二次函数与面积专题Word格式.docx

二次函数与面积专题Word格式.docx

《二次函数与面积专题Word格式.docx》由会员分享，可在线阅读，更多相关《二次函数与面积专题Word格式.docx（17页珍藏版）》请在冰豆网上搜索。

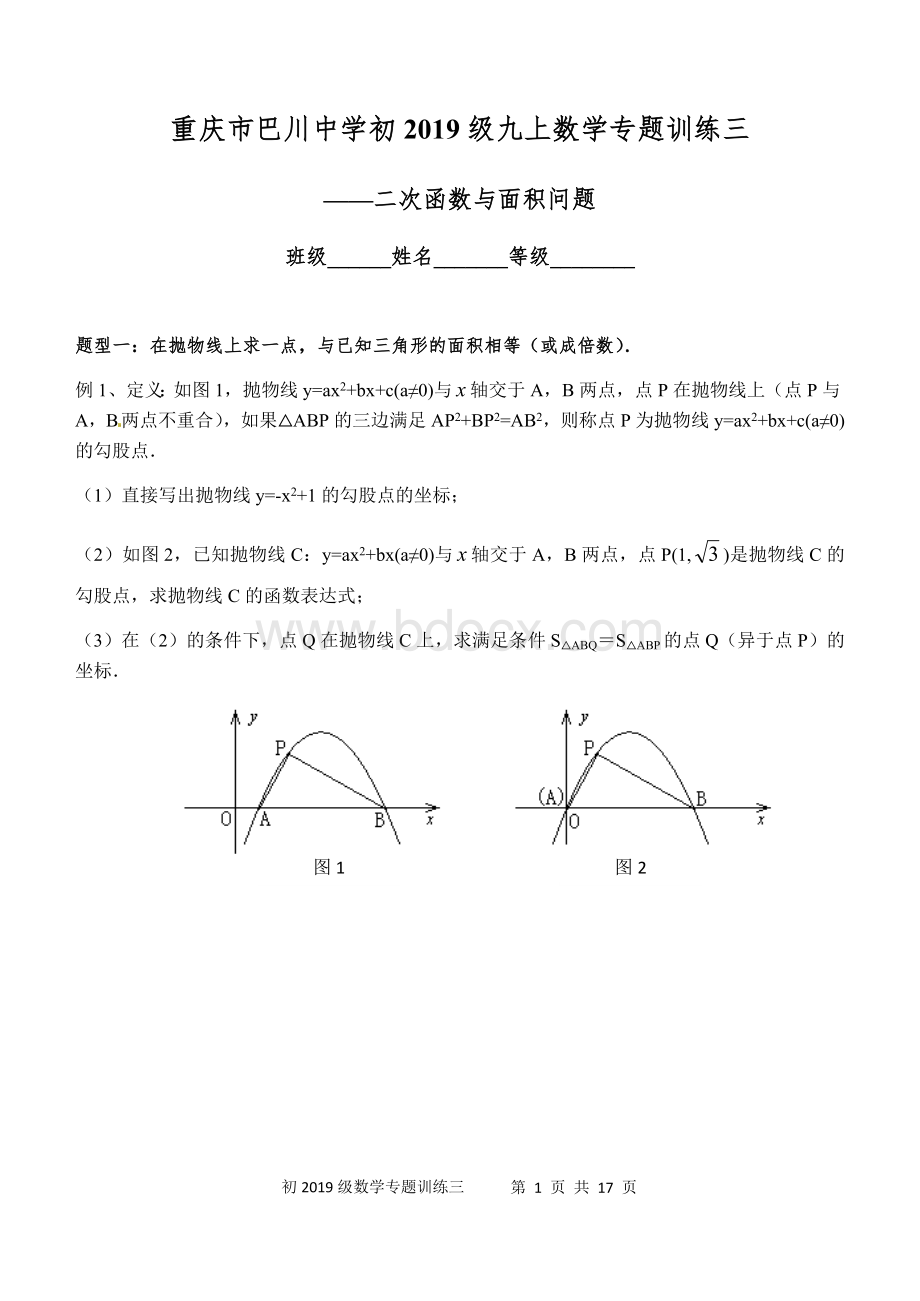
（2）如图2，已知抛物线C：

y=ax2+bx（a≠0）与轴交于A，B两点，点P（1,）是抛物线C的勾股点，求抛物线C的函数表达式；

（3）在

（2）的条件下，点Q在抛物线C上，求满足条件S△ABQ＝S△ABP的点Q（异于点P）的坐标．

图1

图2

练习1.如图，已知抛物线与轴交于点A和点B，与轴交于点C，连接BC交抛物线的对称轴于点E,D是抛物线的顶点．

（1）直接写出点A、B、C、D的坐标，并求出S△ABD；

（2）求出直线BC的解析式；

（3）若点P在第一象限内的抛物线上，且S△ABP＝4S△COE，求P点坐标．

题型二：

已知二定点，在抛物线上求一动点，使三角形面积最大

例2.如图，已知抛物线y=ax2+bx-3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（-1,0），C点坐标是（-4,-3）．

（1）求抛物线的解析式；

（2）若点E是位于直线AC的上方抛物线上的一动点，试求△ACE的最大面积及E点的坐标；

（3）在

（2）的条件下，在抛物线上是否存在异于点E的P点，使S△PAC＝S△EAC，若存在，求出点P的坐标；

若不存在，请说明理由．

A

B

C

x

y

O

变式：

在抛物线上是否存在点P，使S△PAC＝S△ABC，若存在，求出点P的坐标；

[练习]1.如图,已知抛物线y=x2+bx+c与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，-1）.

（2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；

（3）在直线BC上是否存在一点P，使△ACP为等腰三角形，若存在，求点P的坐标，若不存在，说明理由.

2．在平面直角坐标系xoy中，规定：

抛物线y=a（x-h）2+k的伴随直线为y=a（x-h）+k.例如：

抛物线y=2（x+1）2-3的伴随直线为y=2（x+1）-3，即y=2x-1

（1）在上面规定下，抛物线y=（x+1）2-4的顶点为.伴随直线为；

抛物线y=（x+1）2-4与其伴随直线的交点坐标为和；

（2）如图，顶点在第一象限的抛物线y=m（x-1）2-4m与其伴随直线相交于点A,B（点A在点B的右侧）与轴交于点C，D．

①若∠CAB＝90°

求的值；

②如果点P（x,y）是直线BC上方抛物线的一个动点，△PBC的面积记为S，当S取得最大值时，求m的值.

3.抛物线y=ax2+bx+3经过点A（1,0）和点B（5,0）．

（1）求该抛物线所对应的函数解析式；

（2）该抛物线与直线y=0.6x2+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N,连结PC、PD，在点P运动过程中，△PCD的面积是否存在最大值？

若存在，求出这个最大值及P的坐标；

若不存在，说明理由；

（3）在

（2）的条件下，在抛物线上是否存在点Q，使S△QCD=S△PCD，若存在，求出点Q的坐标，若不存在，请说明理由．

4.如图，在平面直角坐标系中，抛物线y=ax2+bx﹣5交y轴于点A，交x轴于点B（﹣5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D．

（1）求此抛物线的表达式；

（2）点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD的面积；

（3）若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，△ABP的面积最大，求出此时点P的坐标和△ABP的最大面积．

题型三：

抛物线中，以面积为条件的几何问题

例3.如图，抛物线y=ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．

（1）求抛物线的函数表达式．

（2）当t为何值时，矩形ABCD的周长有最大值？

最大值是多少？

（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．

练习3:

1.如图，二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC=3，直线l是抛物线的对称轴，E是抛物线的顶点．

（1）求b，c的值；

（2）如图1，连BE，线段OC上的点F关于直线l的对称点F′恰好在线段BE上，求点F的坐标；

（3）如图2，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N．试问：

抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？

若存在，求出点Q的坐标；

若不存在，说明理由．

2.如图，已知二次函数y=ax2+bx+c的图象的顶点坐标为（2，﹣9），该函数的图象与y轴交于点A（0，﹣5），与x轴交于点B，C

（1）求该二次函数的解析式；

（2）求点B的坐标；

（3）过点A作AD∥x轴，交二次函数的图象于点D，M为二次函数图象上一点，设点M的横坐标为m，且0＜m≤5，过点M作MN∥y轴，交AD于点N，连接AM，MD，设△AMD的面积为s．

①求s关于m的函数解析式；

②判断出当点M在何位置时，△AMD的面积最大，并求出最大面积．

3.二次函数y=ax2+bx+6（a≠0）的图象交y轴于C点，交x轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根．

（1）求出点A、点B的坐标及该二次函数表达式．

（2）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．

（3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且MN=，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q．以点P，M，Q，N为顶点的四边形能否为平行四边形？

若能，请求出n的值；

若不能，请说明理由．

4.如图，已知点C（0，3），抛物线的顶点为A（2，0），与y轴交于点B（0，1），F在抛物线的对称轴上，且纵坐标为1．点P是抛物线上的一个动点，过点P作PM⊥x轴于点M，交直线CF于点H，设点P的横坐标为m．

（2）若点P在直线CF下方的抛物线上，用含m的代数式表示线段PH的长，并求出线段PH的最大值及此时点P的坐标；

（3）当PF﹣PM=1时，若将“使△PCF面积为2”的点P记作“巧点”，则存在多个“巧点”，且使△PCF的周长最小的点P也是一个“巧点”，请直接写出所有“巧点”的个数，并求出△PCF的周长最小时“巧点”的坐标．

第17页共17页

初2019级数学专题训练三