全国中考数学100套试题分类汇编四边形综合Word下载.docx

全国中考数学100套试题分类汇编四边形综合Word下载.docx

《全国中考数学100套试题分类汇编四边形综合Word下载.docx》由会员分享，可在线阅读，更多相关《全国中考数学100套试题分类汇编四边形综合Word下载.docx（19页珍藏版）》请在冰豆网上搜索。

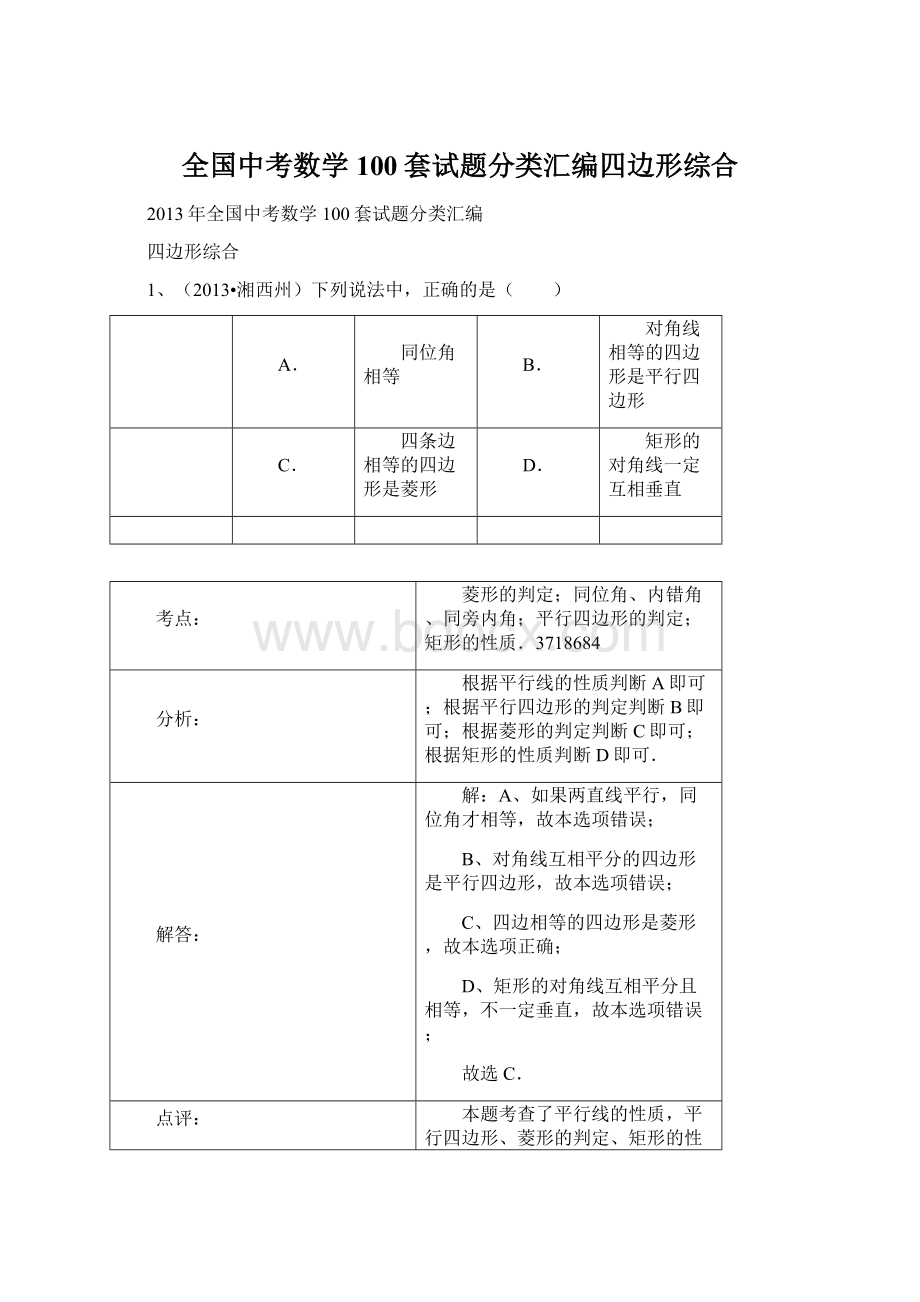
根据菱形的判定判断C即可；

根据矩形的性质判断D即可．

解答：

解：

A、如果两直线平行，同位角才相等，故本选项错误；

B、对角线互相平分的四边形是平行四边形，故本选项错误；

C、四边相等的四边形是菱形，故本选项正确；

D、矩形的对角线互相平分且相等，不一定垂直，故本选项错误；

故选C．

点评：

本题考查了平行线的性质，平行四边形、菱形的判定、矩形的性质的应用，主要考查学生的理解能力和辨析能力．

2、（2013陕西）如图，四边形ABCD的对角线AC、BD相交于点O，且BD平分AC，若BD=8，AC=6，∠BOC=120°

，则四边形ABCD的面积为.（结果保留根号）

三角形面积的求法及特殊角的应用。

解析：

BD平分AC，所以OA=OC=3，因为∠BOC=120°

，

所以∠DOC=∠A0B=60°

，过C作CH⊥BD于H，

过A作AG⊥BD于G，在△CHO中，∠C0H=60°

OC=3，所以CH=，同理：

AG=，

所以四边形ABCD的面积=。

3、（2013河南省）如图，在等边三角形中，,射线，点从点出发沿射线以的速度运动，同时点从点出发沿射线以的速度运动，设运动时间为

（1）连接，当经过边的中点时，求证：

证明：

∵

∴

∵是边的中点

又∵

（2）填空：

①当为s时，四边形是菱形；

②当为s时，以为顶点的四边形是直角梯形。

【解析】①∵当四边形是菱形时，∴

由题意可知：

，∴

②若四边形是直角梯形，此时

过作于M，，可以得到，

即，∴，

此时，重合，不符合题意，舍去。

若四边形若四边形是直角梯形，此时，

∵△ABC是等边三角形，F是BC中点，

∴，得到

经检验，符合题意。

【答案】①②

4、（2013•德州）

（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：

BE=CD；

（尺规作图，不写做法，保留作图痕迹）；

（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？

简单说明理由；

（3）运用

（1）、

（2）解答中所积累的经验和知识，完成下题：

如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°

，∠CAE=90°

，AB=BC=100米，AC=AE，求BE的长．

四边形综合题．

专题：

计算题．

（1）分别以A、B为圆心，AB长为半径画弧，两弧交于点D，连接AD，BD，同理连接AE，CE，如图所示，由三角形ABD与三角形ACE都是等边三角形，得到三对边相等，两个角相等，都为60度，利用等式的性质得到夹角相等，利用SAS得到三角形ABD与三角形ACE全等，利用全等三角形的对应边相等即可得证；

（2）BE=CD，理由与

（1）同理；

（3）根据

（1）、

（2）的经验，过A作等腰直角三角形ABD，连接CD，由AB=AD=100，利用勾股定理求出BD的长，由题意得到三角形DBC为直角三角形，利用勾股定理求出CD的长，即为BE的长．

（1）完成图形，如图所示：

证明：

∵△ABD和△ACE都是等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAE=60°

∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，

∵在△CAD和△EAB中，

∴△CAD≌△EAB（SAS），

∴BE=CD；

（2）BE=CD，理由同

（1），

∵四边形ABFD和ACGE均为正方形，

∴AD=AB，AC=AE，∠BAD=∠CAE=90°

∴∠CAD=∠EAB，

（3）由

（1）、

（2）的解题经验可知，过A作等腰直角三角形ABD，∠BAD=90°

则AD=AB=100米，∠ABD=45°

∴BD=100米，

连接CD，则由

（2）可得BE=CD，

∵∠ABC=45°

，∴∠DBC=90°

在Rt△DBC中，BC=100米，BD=100米，

根据勾股定理得：

CD==100米，

则BE=CD=100米．

此题考查了四边形综合题，涉及的知识有：

全等三角形的判定与性质，等边三角形，等腰直角三角形，以及正方形的性质，勾股定理，熟练掌握全等三角形的判定与性质是解本题的关键．

5、（2013•绍兴）若一个矩形的一边是另一边的两倍，则称这个矩形为方形，如图1，矩形ABCD中，BC=2AB，则称ABCD为方形．

（1）设a，b是方形的一组邻边长，写出a，b的值（一组即可）．

（2）在△ABC中，将AB，AC分别五等分，连结两边对应的等分点，以这些连结为一边作矩形，使这些矩形的边B1C1，B2C2，B3C3，B4C4的对边分别在B2C2，B3C3，B4C4，BC上，如图2所示．

①若BC=25，BC边上的高为20，判断以B1C1为一边的矩形是不是方形？

为什么？

②若以B3C3为一边的矩形为方形，求BC与BC边上的高之比．

四边形综合题．3718684

（1）答案不唯一，根据已知举出即可；

（2）①求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4，推出==，==，==，==，求出B1C1=5，B2C2=10，B3C3=15，B4C4=20，AE=4，AH=8，AG=12，AN=16，MN=GN=GH=HE=4，BQ=B2O=B3Z=B4K=4，根据已知判断即可；

②设AM=h，根据△ABC∽△AB3C3，得出==，求出MN=GN=GH=HE=h，分为两种情况：

当B3C3=2×

h，时，当B3C3=×

h时，代入求出即可．

（1）答案不唯一，如a=2，b=4；

（2）①以B1C1为一边的矩形不是方形．

理由是：

过A作AM⊥BC于M，交B1C1于E，交B2C2于H，交B3C3于G，交B4C4于N，则AM⊥B4C4，AM⊥B3C3，AM⊥B2C2，AM⊥B1C1，

∵由矩形的性质得：

BC∥B1C1∥B2C2∥B3C3∥B4C4，

∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4，

∴=，==，==，==，

∵AM=20，BC=25，

∴B1C1=5，B2C2=10，B3C3=15，B4C4=20，AE=4，AH=8，AG=12，AN=16，

∴MN=GN=GH=HE=4，

∴BQ=B2O=B3Z=B4K=4，

即B1C1≠2B1Q，B1Q≠2B1C1，

∴以B1C1为一边的矩形不是方形；

②∵以B3C3为一边的矩形为方形，设AM=h，

∴△ABC∽△AB3C3，

∴==，

则AG=h，

∴MN=GN=GH=HE=h，

h，时，=；

当B3C3=×

h时，=．

综合上述：

BC与BC边上的高之比是或．

本题考查了相似三角形的性质和判定和矩形的性质的应用，注意：

相似三角形的对应高的比等于相似比．

6、（2013•资阳）在一个边长为a（单位：

cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．

（1）如图1，当点M与点C重合，求证：

DF=MN；

（2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以cm/s速度沿AC向点C运动，运动时间为t（t＞0）；

①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．

②连结FM、FN，△MNF能否为等腰三角形？

若能，请写出a，t之间的关系；

若不能，请说明理由．

四边形综合题

（1）证明△ADF≌△DNC，即可得到DF=MN；

（2）①首先证明△AFE∽△CDE，利用比例式求出时间t=a，进而得到CM=a=CD，所以该命题为真命题；

②若△MNF为等腰三角形，则可能有三种情形，需要分类讨论．

（1）证明：

∵∠DNC+∠ADF=90°

，∠DNC+∠DCN=90°

∴∠ADF=∠DCN．

在△ADF与△DNC中，

∴△ADF≌△DNC（ASA），

∴DF=MN．

（2）解：

①该命题是真命题．

理由如下：

当点F是边AB中点时，则AF=AB=CD．

∵AB∥CD，∴△AFE∽△CDE，

∴，

∴AE=EC，则AE=AC=a，

∴t==a．

则CM=1•t=a=CD，

∴点M为边CD的三等分点．

②能．理由如下：

易证AFE∽△CDE，∴，即，得AF=．

易证△MND∽△DFA，∴，即，得ND=t．

∴ND=CM=t，AN=DM=a﹣t．

若△MNF为等腰三角形，则可能有三种情形：

（I）若FN=MN，则由AN=DM知△FAN≌△NDM，

∴AF=DM，即=t，得t=0，不合题意．

∴此种情形不存在；

（II）若FN=FM，由MN⊥DF知，HN=HM，∴DN=DM=MC，

∴t=a，此时点F与点B重合；

（III）若FM=MN，显然此时点F在BC边上，如下图所示：

易得△MFC≌△NMD，∴FC=DM=a﹣t；

又由△NDM∽△DCF，∴，即，∴FC=．

∴=a﹣t，

∴t=a，此时点F与点C重合．

综上所述，当t=a或t=a时，△MNF能够成为等腰三角形．

本题是运动型几何综合题，考查了相似三角形、全等三角形、正方形、等腰三角形、命题证明等知识点．解题要点是：

（1）明确动点的运动过程；

（2）明确运动过程中，各组成线段、三角形之间的关系；

（3）运用分类讨论的数学思想，避免漏解．

7、（2013•宁波）若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．

（1）如图1，在梯形ABCD中，AD∥BC，∠BAD=120°

，∠C=75°

，BD平分∠ABC．求证：

BD是梯形ABCD的和谐线；

（2）如图2，在12×

16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；

（3）四边形ABCD中，AB=AD=BC，∠BAD=90°

，AC是四边形ABCD的和谐线，求∠BCD的度数．

（1）要证明BD是四边形ABCD的和谐线，只需要证明△ABD和△BDC是等腰三角形就可以；

（2）根据扇形的性质弧上的点到顶点的距离相等，只要D在上任意一点构成的四边形ABDC就是和谐四边形；

连接BC，在△BAC外作一个以AC为腰的等腰三角形ACD，构成的四边形ABCD就是和谐四边形，

（3）由AC是四边形ABCD的和谐线，可以得出△ACD是等腰三角形，从图4，图5，图6三种情况运用等边三角形的性质，正方形的性质和30°

的直角三角形性质就可以求出∠BCD的度数．

（1）∵AD∥BC，

∴∠ABC+∠BAD=180°

，∠ADB=∠DBC