初中数学应用题含答案及解析Word文档格式.docx
《初中数学应用题含答案及解析Word文档格式.docx》由会员分享,可在线阅读,更多相关《初中数学应用题含答案及解析Word文档格式.docx(48页珍藏版)》请在冰豆网上搜索。
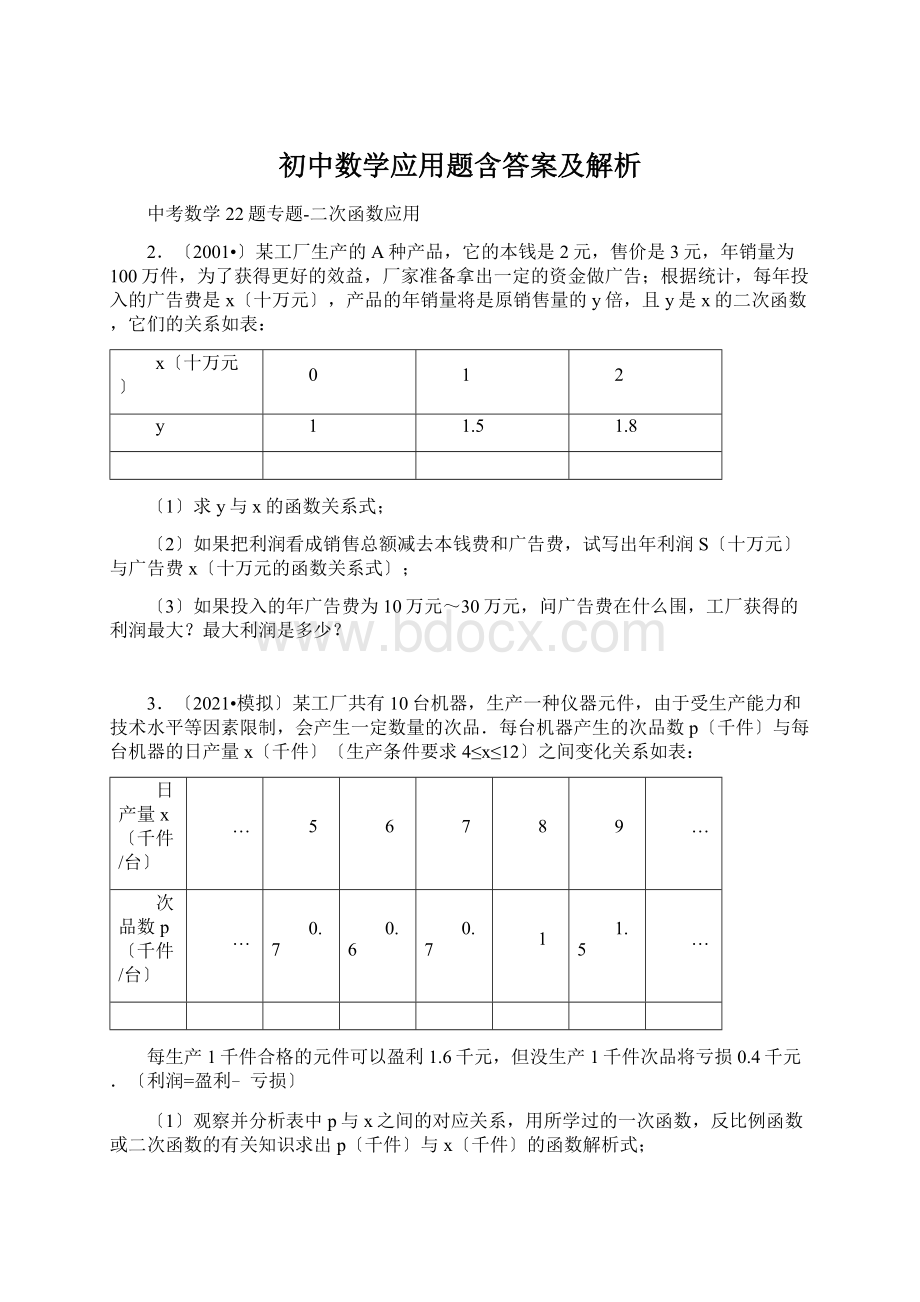
…
5
6
7
8
9
次品数p〔千件/台〕
0.7
0.6
每生产1千件合格的元件可以盈利1.6千元,但没生产1千件次品将亏损0.4千元.〔利润=盈利﹣亏损〕
〔1〕观察并分析表中p与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识求出p〔千件〕与x〔千件〕的函数解析式;
〔2〕设该工厂每天生产这种元件所获得的利润为y〔千元〕,试将y表示x的函数;
并求当每台机器的日产量x〔千件〕为多少时所获得的利润最大,最大利润为多少?
4.〔2021•乌鲁木齐〕某公司销售一种进价为20元/个的计算机,其销售量y〔万个〕与销售价格x〔元/个〕的变化如下表:
价格x〔元/个〕
30
40
50
60
销售量y〔万个〕
4
3
同时,销售过程中的其他开支〔不含造价〕总计40万元.
〔1〕观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y〔万个〕与x〔元/个〕的函数解析式.
〔2〕求出该公司销售这种计算器的净得利润z〔万个〕与销售价格x〔元/个〕的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
〔3〕该公司要求净得利润不能低于40万元,请写出销售价格x〔元/个〕的取值围,假设还需考虑销售量尽可能大,销售价格应定为多少元?
5.〔2021•沙市区三模〕某公司准备购进一批产品进展销售,该产品的进货单价为6元/个.根据市场调查,得到了四组关于日销售量y〔个〕与销售单价x〔元/个〕的数据,如表
x
10
12
14
16
300
240
180
120
〔1〕如果在一次函数、二次函数和反比例函数这三个函数模型中,选择一个来描述日销售量与销售单价之间的关系,你觉得哪个适宜?
并写出y与x之间的函数关系式〔不要求写出自变量的取值围〕
〔2〕按照〔1〕中的销售规律,请你推断,当销售单价定为17.5元/个时,日销售量为多少?
此时,获得日销售利润是多少?
〔3〕为了防风险,该公司将日进货本钱控制在900元〔含900元〕以,按照〔1〕中的销售规律,要想获得的日销售利润最大,那么销售单价应定为多少?
并求出此时的最大利润.
6.〔2021•新区二模〕某企业信息部进展市场调研发现:
信息一:
如果单独投资A种产品,所获利润yA〔万元〕与投资金额x〔万元〕之间存在某种关系的局部对应值如下表:
x〔万元〕
2.5
yA〔万元〕
0.4
0.8
1.2
信息二:
如果单独投资B种产品,那么所获利润yB〔万元〕与投资金额x〔万元〕之间存在二次函数关系:
yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
〔1〕求出yB与x的函数关系式;
〔2〕从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式;
〔3〕如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
7.“哪里的民营经济开展得好,哪里的经济就越兴旺.〞恒强科技公司在市委市政府这一执政理念的鼓舞下,在已有高科技产品A产生利润的情况下,决定制定一个开发利用高科技产品B的10年开展规划,该规翘晦年的专项投资资金是50万元,在前五年,每年从专项资金中最多拿出25万元投入到产品A使它产生利润,剩下的资金全部用于产品B的研发.经测算,每年投入到产品A中x万元时产生的利润y1〔万元〕满足下表的关系
10
20
30
40
y1〔万元〕
从第六年年初开场,产品B已研发成功,在产品A继续产生利润的同时产品B也产生利润,每年投入到产品B中x万元时产生的利润y2〔万元〕满足.
〔1〕请观察题目中的表格,用所学过的一次函数、二次函数或反比例函数的相关知识,求出y1与x的函数关系式?
〔2〕按照此开展规划,求前5年产品A产生的最大利润之和是多少万元?
〔3〕后5年,专项资金全部投入到产品A、产品B使它们产生利润,求后5年产品A、产品B产生的最大利润之和是多少万元?
8.某农户生产经销一种农副产品,这种产品的本钱价为20元/千克.而且物价部门规定这种产品的销售价不得高于28元/千克,通过市场调查发现,该产品每天的销售量w〔千克〕与销售价x〔元/千克〕的变化如下表:
销售价x〔元/千克〕
21
23
25
27
销售量w〔千克〕
38
34
26
设这种产品每天的销售利润为y〔元〕.
〔1〕请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出w与x所满足的函数关系式,并求出y与x所满足的函数关系式;
〔2〕当销售价定为多少元时,每天的销售利润最大?
〔3〕该农户想要每天获得150元的销售利润,销售价应定为多少元?
9.某商品每件本钱60元,试销阶段每件商品的销售价x〔元〕与商品的日销售量y〔件〕之间的关系如下表,其中日销售量y是销售价x的函数.
x〔元〕
65
70
y〔件〕
100
80
〔1〕请判断这种函数是一次函数、反比例函数,还是二次函数?
并求出函数解析式;
〔2〕要使每日的销售利润最大,每件商品的销售价应定为多少元?
此时每日销售利润是多少?
〔3〕要使这种商品每日的销售利润不低于600元,且每件商品的利润率不得高于40%,那么该商品的销售价x应定为多少?
请直接写出结果.
10.某厂设计了一款本钱为20元∕件的公益用品投放市场进展试销.经过调查,得到如下数据:
销售单价x〔元∕件〕
每天销售量y〔件〕
500
400
200
〔1〕认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y与x的函数关系,并求出函数关系式.
〔2〕当销售单价定为多少时,该厂试销该公益品每天获得的利润最大?
〔利润=销售总价﹣本钱总价〕
〔3〕当地民政部门规定,假设该厂销售此公益品单价不低于本钱价且不超过46元/件时,该厂每销售一件此公益品,国家就补贴该厂a元利润〔a>4〕,公司通过销售记录发现,日销售利润随销售单价的增大而增大,求a的取值围.
11.〔2021•模拟〕阅读以下文字
2021年亚运会前夕某公司生产一种时令商品每件本钱为20元,经市场发现该商品在未来40天的日销售量为a件,与时间t天的关系如下表:
时间t〔天〕
36
日销售量a〔件〕
94
90
84
76
24
未来40天,前20天每天的价格b〔元/件〕与时间t的关系为b=t+25〔1≤t≤20〕,后20天每天价格为c〔元/件〕与时间t的关系式为c=﹣t+40〔21≤t≤40〕解得以下问题
〔1〕分析表中的数据,用所学过的一次函数,二次函数,反比例函数知识确定一个满足这些数据的a与t的函数关系式;
〔2〕请预测未来40天中哪一天日销售利润最大,最大日销售利润是多少?
〔3〕在实际销售的前20天中该公司决定销售一件就捐赠n元〔n<4〕利润给亚运会组委会,通过销售记录发现前20天中,每天扣除捐赠后利润随时间t的增大而增大,求n的取值围.
12.2021年11月4日,市人民政府新闻办宣布迪斯尼工程报告已获国家有关部门核准.相应的周边城市效应也随即带动,某周边城市方案开通至的磁悬浮列车,列车走完全程包含启动加速、均匀运行、制动减速三个阶段,磁悬浮列车从启动加速到稳定匀速运行共需200秒,在这段时间的相关数据如表所示:
时间t〔秒〕
0
50
100
150
200
速度V〔米/秒〕
0
60
90
120
路程s〔米〕
750
3000
6750
12000
〔1〕请你在一次函数、二次函数和反比例函数中选择适宜的函数来分别表示在加速阶段〔0≤t≤200〕速度v与时间t的函数关系,路程s与时间t的函数关系.
〔2〕最新研究说明,此种列车的稳定运行速度可达180米/秒,为了检测稳定运行时各项指标,在列车到达这一速度后至少要运行100秒,才能收集全相关数据.假设在加速过程中,路程、速度随时间的变化关系任然满足〔1〕中的函数关系式,并且制动减速所需路程与启动加速的路程一样,根据以上要求,至少要建多长的轨道才能满足实验检测要求?
13.〔2021•蕲春县模拟〕今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数x
价格y〔元/千克〕
2.2
2.4
2.6
〔1〕请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式;
〔2〕进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y〔元/千克〕从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=﹣x2+bx+c,请求出5月份y与x的函数关系式;
〔3〕假设4月份此种蔬菜的进价m〔元/千克〕与周数x所满足的函数关系为m=x+1.2,5月份此种蔬菜的进价m〔元/千克〕与周数x所满足的函数关系为m=x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?
且最大利润分别是多少?
14.〔2021•宜兴市模拟〕在气候对人类生存压力日趋加大的今天,开展低碳经济,全面实现低碳生活逐渐成为人们的共识,某企业采用技术革新,节能减排,今年前5个月二氧化碳排放量y〔吨〕与月份x〔月〕之间的关系如下表:
月份x〔月〕
二氧化碳排放量y〔吨〕
48
46
44
42
〔1〕请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数关系能表示y和x的变化规律,请写出y与x的函数关系式;
〔2〕随着二氧化碳排放量的减少,每排放一吨二氧化碳,企业相应获得的利润也有所提高,且相应获得的利润p〔万元〕与月份x〔月〕的函数关系如下图,那么