中学数学之经典案例Word文档下载推荐.docx

中学数学之经典案例Word文档下载推荐.docx

《中学数学之经典案例Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《中学数学之经典案例Word文档下载推荐.docx（6页珍藏版）》请在冰豆网上搜索。

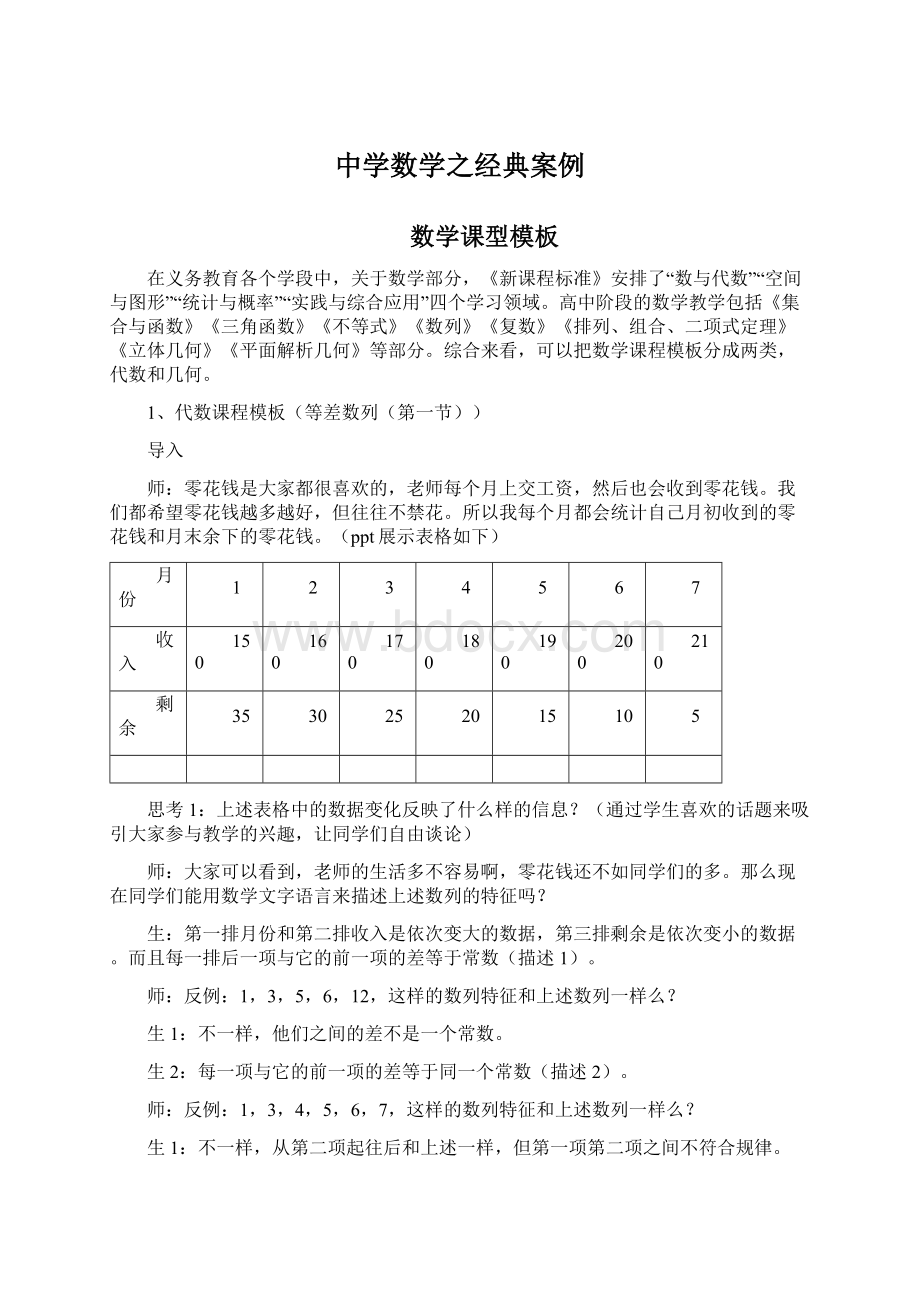
收入

150

160

170

180

190

200

210

剩余

35

30

25

20

15

10

思考1：

上述表格中的数据变化反映了什么样的信息？

（通过学生喜欢的话题来吸引大家参与教学的兴趣，让同学们自由谈论）

大家可以看到，老师的生活多不容易啊，零花钱还不如同学们的多。

那么现在同学们能用数学文字语言来描述上述数列的特征吗？

生：

第一排月份和第二排收入是依次变大的数据，第三排剩余是依次变小的数据。

而且每一排后一项与它的前一项的差等于常数（描述1）。

反例：

1，3，5，6，12，这样的数列特征和上述数列一样么？

生1：

不一样，他们之间的差不是一个常数。

生2：

每一项与它的前一项的差等于同一个常数（描述2）。

1，3，4，5，6，7，这样的数列特征和上述数列一样么？

不一样，从第二项起往后和上述一样，但第一项第二项之间不符合规律。

从第二项起，每一项与它的前一项的差等于同一个常数。

（描述3）

（把学生的回答写在黑板上，通过反例的说明，让学生深刻的理解这三组数列的共同特征：

1、前后项为同一常数，2、从第二项起）

新授

用数学符号语言：

生3：

-=d

等价么？

生4：

应加上（d是常数）n≥2,n∈N*

（让学生充分进行讨论，注意文字描述与符号描述的严谨性）

对式子进行变形可得：

=+d（d是常数）n≥2,n∈N*，如果我们能跳出d的思维定势，能得到很多的公式变形。

（为今后更好的研究其特征，埋下伏笔）

这样的数列在你日常生活中存在？

1，3，7，7，9，11，·

·

d=1

10，15，20，25，30，35，40，·

d=5

（让学生举例，加深对数列的感性认识）

满足这样特征的数列很多，所以我们有必要为这样的数列取一个名字？

等差数列

（让学生给出数学的定义，并有自己的语言进行交流。

当然也允许学生提出“等加数列”等的说法，教师可进行比较，差有利于加一加进行消项等）

定义：

一般的，如果一个数列从第二项起，每一项与前一项的差等于同一个常数，那么这个数列就叫等差数列，d为公差。

为数列的首项。

，，，·

（n≥2,,n∈N*）

（对定义进行分析，强调：

1、同一常数，2、从第二项起。

同时在学生的举例中改动几个数，问学生破坏定义的什么要求，注意对数列概念的严谨性分析。

）

回到表格中抽象出的3个数列，分别说明他们的公差。

d=1d=10d=-5

（引导学生发现公差d对数列的影响，当d>

0时数列是递增，当d<

0时数列是递减，当d=0时数列是常数列。

见上表，请7号的同学回答a7，请8号的同学求a8，请42号的同学求a42·

若能求出数列的通项公式，问题就能较好的解决；

（再提出问题，引导问题进一步发展，发现求通项的必要性）

我们把问题推广到一般情况。

若一个数列，，，·

，an，·

是等差数列，它的公差是d，那么数列{an}的通项公式是什么？

方法1．n=2

n=3

n=4

当n=1时，也成立。

（归纳、猜想。

培养学生合情推理的能力）

方法2。

用叠加得，当n=1时，也成立。

整理得：

n∈N*

（回过来再说明等差的优点，体现用等差概念的优势，化繁为简，化腐朽为神奇，体现“数学之美”；

并让学生自由的交流，进行“再创造”）可推出，n、m∈N*

1、对通项公式进行分析；

通项公式中含有a1，d，n，an四个量，其中a1和d是基本量，当a1和d确定后，通项公式便随之确定．从已知和未知的角度看，若已知其中任意三个量的值，即可利用方程的思想求出第四个量的值（即知三求一）

2、，n、m∈N*

挖掘等差数列的函数特征：

等差数列的通项公式an=a1＋（n－1）d．可表示为an=dn＋c（其中c=a1－d，n属于N*）的形式，n的系数即为公差．当d≠0时，an是定义在自然数集上的一次函数，其图象是一次函数y=dx＋c（x属于R）的图象上的一群孤立的点．（画图略）

（在数列的通项公式中，每取一个n，都有唯一一个an与之对应，让学生联系映射的思想，挖掘数列的函数特征）

巩固：

回到表格中抽象出的4个数列，分别说明他们的通项公式。

=1+（n-1）=n

=150+（n-1）*10

=35+（n-1）*（-5）

小结：

这节课我们一起对生活中常见的一类数据，进行了一次有意义的探索，并总结等差数列的概念求出了等差数列的通项公式，等差数列的定义是判断一个数列是否是等差数列的依据之一，通项公式是通项an与项数n的关系的一种解析表示，它从函数和方程两个角度为我们求解问题提供了有力的工具．通过给等差数列下定义及自行探求通项公式，使我们领略了合情推理与逻辑推理在探索、发现知识方面的重要作用．让学生明白“数学来源于生活，应用于生活”。

作业：

等差数列有很多的性质，请同学们回去后对等差数列的性质进行研究？

在生活中寻找一些数据进行一次探索？

（研究性作业）

说明：

导入和新授之间只要过度自然即可，导入环节不超过1-2分钟。

上述详案，标注括号的部分在试讲过程中，可以根据实际情况和时间不完全说出来。

整个教学过程凸显学生为主体，引导学生“说出“教学过程。

板书可以在讲课过程中适当写出，布置作业环节要体现开放性。

2、几何课程模板（圆柱的认识）

上节课我们学习了长方体，咱们简单的回顾一下。

首先我们教师里面有哪些东西是正方体长方体，他们有哪些方面的性质？

长方体的组成，就是长方体有6个面，12条棱和8个顶点。

相对的面的面积相等，相对的棱的长度相等，比如教师里面立着的空调就是一个长方体。

回答的很好，学习几何是很有意思的，它常常和我们的生活联系在一起。

再看一下老师手里的杯子，大家来描述一下，它是什么形状？

圆圆的，像个圆筒一样。

回答的很好，现在请大家想一下，生活中还有那些物体也是这种样子的形状？

超市里面的灌装可乐。

教室里面日光灯灯管。

很好，你们很善于观察生活。

刚刚大家列举的物体，圆筒一样的形状，我们称之为圆柱。

请大家拿出学具，圆柱体模型，观察并想一想圆柱有哪些特征？

圆柱有三部分组成，两个圆和一个周围的面。

两个圆的面积相等，

圆柱有无数条高。

你能给大家指一指圆柱的高在哪里吗？

（学生指）

教师划一条侧面上的斜线，这是圆柱的高吗？

为什么？

两个底面圆心的连线是高吗？

高有多少条？

大家的观察很仔细，确实圆柱是由三部分组成的，两个圆和一个曲面，并且两个圆的面积相等，在圆柱中，两个圆叫圆柱的底面，曲面叫做圆柱的侧面，圆柱有无数条高。

（板书）

通过刚才的研究，我们知道：

圆柱是有两个完全一样的圆和一个侧面组成的，是不是任意两个完全相等的圆和一个侧面就一定能组成圆柱呢？

（不是）我这里有两个大小完全相同的圆和一个侧面，他们能不能组成一个圆柱呢？

（不能）

圆柱的底面和侧面之间又有什么样的关系呢？

请大家以小组为单位，结合手中的学具进行研究。

圆的大小和侧面的粗细一样。

大家的感觉没错。

可是老师总感觉底面圆和侧面之间的关还不够具体，谁有办法能让大家很容易的看到它们之间的关系？

再次进行小组合作。

组1：

我们可以把圆柱的侧面剪开，把它展开后就变成了一个长方形。

这样它们就都成了平面图形，就容易进行比较了。

这个小组的同学把侧面展开变成了长方形，是沿哪里剪开的？

（圆柱的高）这样就把侧面这一曲面转变成了平面。

板书：

化曲为直

在以前的学习中，还有哪些知识也用到了这一方法？

学习圆的周长时我们也是用到了这一思想。

学习圆的面积时我们也是用到了这一思想，把原转化成了近似的长方形。

大家的想法很有创造力，那展开后的长方形和底面圆之间有什么关系？

组2：

现在长方形的长等于圆柱的底面周长。

大家把展开的圆柱体再围起来，验证一下这位同学的结果。

（学生操作）

还有其他发现吗？

长方形的宽等于圆柱的高。

现在谁能完整地说一说展开后的长方形和圆柱的关系？

生5：

圆柱的侧面展开后是一个长方形，长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高。

师：

刚才通过大家的努力，我们发现了圆柱的基本特征。

现在给大家分小组，每小组发两张白纸，大家自己尝试一下做一个白纸。

并测量出自己制作的圆柱的各个数据。

我们组是利用长62.8厘米求出了底面圆的周长也是62.8厘米，62.8÷

3.14÷

2=10厘米，所以底面圆的半径是10厘米。

用圆规画出了两个圆。

粘起来就做成了一个圆柱。

我们是把31.4厘米作为圆柱的底面周长，求出底面半径是5厘米，用圆规画出了两个圆做成了圆柱。

小结；

请大家把做成的圆柱举起来互相欣赏一下。

虽然两个小组做成的圆柱形状不同，但他们都用到了今天所学的圆柱的基本特征：

圆柱由两个完全相等的圆和一个侧面围成的，圆柱的侧面展开后是一个长方形，长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高。

练习

大家在课堂上面表现的很好，对圆柱模型的研究也很深入，请大家课后在生活中寻找一个圆柱形的物体，并对他的高和底面进行测量，想一想，如果想知道圆柱的面积，可以怎么算。

几何课程可以尽量使用模型并结合到实际生活，使课程的设计更有创意。