高考名师推荐全国通用高考总复习数学文理全真模拟试题及答案解析三Word下载.docx

高考名师推荐全国通用高考总复习数学文理全真模拟试题及答案解析三Word下载.docx

《高考名师推荐全国通用高考总复习数学文理全真模拟试题及答案解析三Word下载.docx》由会员分享，可在线阅读，更多相关《高考名师推荐全国通用高考总复习数学文理全真模拟试题及答案解析三Word下载.docx（15页珍藏版）》请在冰豆网上搜索。

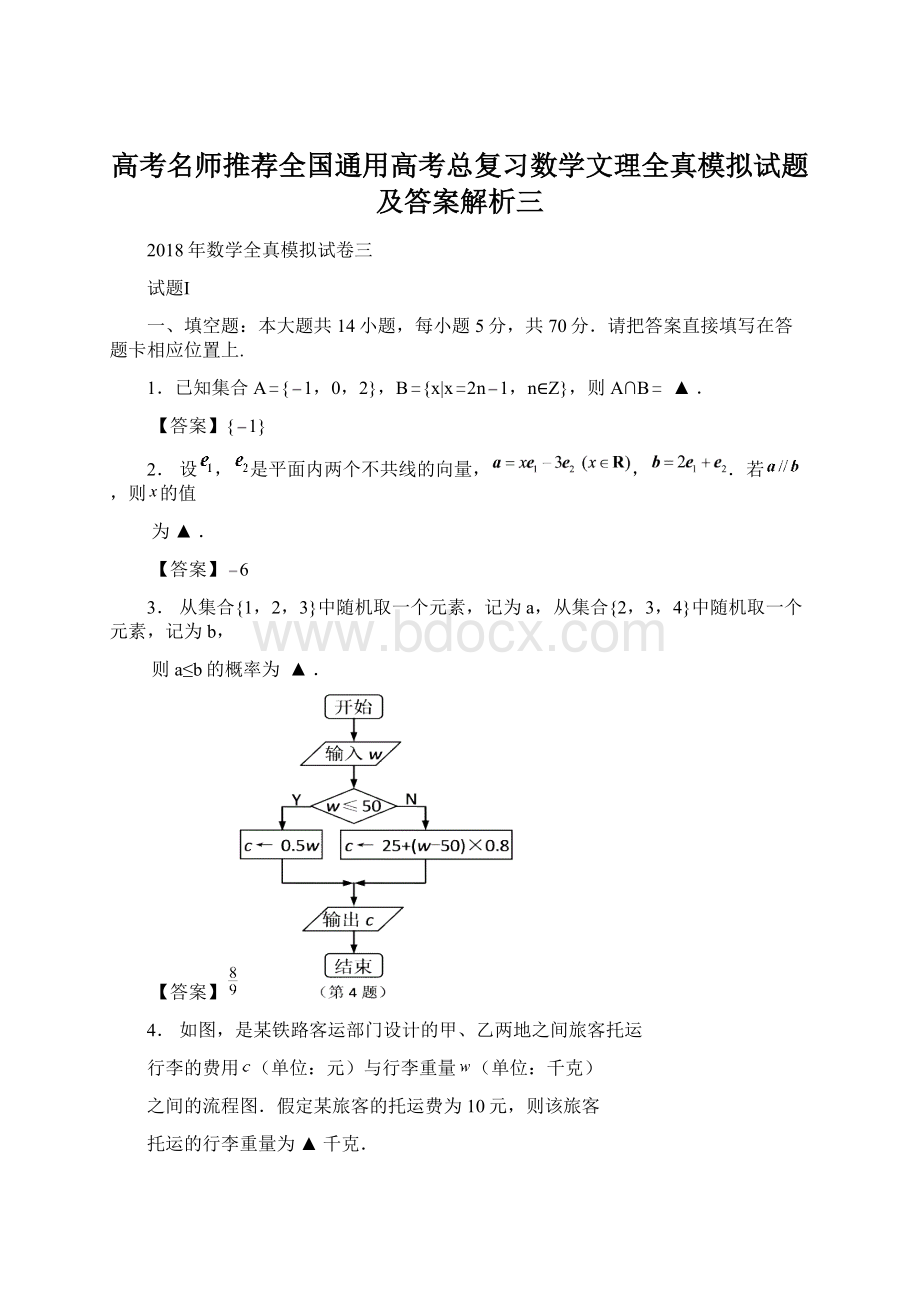
的第一个极值点为，则函数的最小正周期为▲．

9．关于定义在上的函数，给出下列三个命题：

①若，则不是奇函数；

②若，则在上不是单调减函数；

③若对任意的恒成立，则是周期函数．

其中所有正确的命题序号是▲．

【答案】②③

10．已知数列的前项和，且既不是等差数列，也不是等比数列，则的

取值集合是▲．

【答案】．

【解析】．

11．如果将直线：

向左平移1个单位，再向下平移2个单位，所得直线与圆：

相切，则实数的值构成的集合为▲．

【答案】{，}

【解析】易得直线：

，即，圆：

的圆心到直线：

的距离，解得或．

12．已知正数x，y满足，则y的最大值为▲．

【答案】

【解析】由，得，

所以，从而，解得．

13．考察下列等式：

，

……

，

其中为虚数单位，an，bn（n）均为实数．由归纳可得，a2015b2015的值为▲．

【答案】0

【解析】通过归纳可得，，从而a2015b2015

0．

14．在△ABC中，，．设，交于点，且，

（,）,则的值为▲．

【解析】不妨考虑等腰直角三角形ABC，设AB，，

以AB，分别为轴，轴建立平面直角坐标系，

则A，，，，，

直线的方程为：

，①

，②

由①②得，，，所以，

代入，得，，，

解得，，故．

二、解答题：

本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证

明过程或演算步骤．

15．（本题满分14分）

已知△ABC内接于单位圆（半径为1个单位长度的圆），且．

（1）求角的大小；

（2）求△ABC面积的最大值．

（1）由得，

所以，（4分）

故△ABC中，，（6分）

（2）由正弦定理得，即，（8分）

由余弦定理得，即，（10分）

由得，（当且仅当时取等号）（12分）

所以.（14分）

16．（本题满分14分）

如图，在四棱锥中，锐角三角形所

在的平面与底面垂直，．

（1）求证：

平面；

（2）求证：

平面．

证明：

（1）在平面内过点作于，

因为平面平面，平面平面，平面，

所以平面，（4分）

而平面，所以，

由得，

又，平面，

所以平面，（8分）

（2）因为平面，故，

故在平面中，，（11分）

又平面，平面，

所以平面．（14分）

17．（本题满分14分）

某公司设计如图所示的环状绿化景观带，该景观带的内圈由两条平行线段（图中的AB，DC）

和两个半圆构成，设ABxm，且．

（1）若内圈周长为400 

m，则x取何值时，矩形ABCD的面积最大？

（2）若景观带的内圈所围成区域的面积为 

m2，则x取何值时，内圈周长最小？

【解】设题中半圆形半径为r（m），

矩形ABCD的面积为S（m2），

内圈周长为c（m）．

（1）由题意知：

，且

，即，

于是（m2）

当且仅当（m）时，等号成立．

答：

当x100（m）时，矩形ABCD的面积最大．（6分）

（2）由题意知：

，于是，

从而 

．（8分）

因为，所以，即，

解得，所以，（10分）

故．

因为，（12分）

所以关于r的函数在上是单调减函数．

故当即（m）时，内圈周长c取得最小值，

且最小值为（m）．（14分）

18．（本题满分16分）

在平面直角坐标系中，设椭圆：

的焦距为，且过点．

（1）求椭圆的方程；

（2）设点是椭圆上横坐标大于2的一点，过点作圆的两条切线分别与

轴交于点，，试确定点的坐标，使得△的面积最大．

解：

（1）由题意得，，且，（2分）

又，

故，，

所以椭圆的方程为；

（5分）

（2）设点，其中，且，又设，，不妨，

则直线的方程为：

则圆心到直线的距离为，

化简得，（8分）

同理，，

所以，为方程的两根，

则，（10分）

又△的面积为，

所以，（12分）

令，记，

则在恒成立，

所以在上单调递增，

故，即时，最大，

此时△的面积最大．（16分）

19．（本题满分16分）

已知函数，．

（1）若有极值，求a的取值范围；

（2）若有经过原点的切线，求a的取值范围及切线的条数，并说明理由．

（1）易得，（2分）

若，则，从而无极值；

若a>

0，则当时，；

时，，此时有极小值．

综上，a的取值范围是．（4分）

（2）设P（x0，y0）是经过原点的切线与函数图象的切点，

则切线方程为，（6分）

因为切线过点（0，0），于是，即，

因为，所以，

设，则，得，（8分）

x

（0，1）

1

（1，）

+

-

g（x）

↗

极大值1

↘

故当，即时，不存在切线；

当或，即或a<

0时，有且仅有一条切线，

当，即时，存在两条切线，（12分）

下证：

对任意的，在（0，1）内一定有一解，其中．

证明在（0，1）内有一解，

证明在内有一解．

令，

则h

（1）m–10，

这是关于n的二次函数，所以当n充分大时，一定取得正值，

由介值定理知，在内有唯一解，即证．（16分）

20．（本题满分16分）

已知数列的通项公式，．设，，…，（其中…，

）成等差数列．

（1）若．

①当，，为连续正整数时，求的值；

②当时，求证：

为定值；

（2）求的最大值．

解：

（1）①依题意，，，成等差数列，即，

从而，

当为奇数时，解得，不存在这样的正整数；

当为偶数时，解得，所以．（3分）

②依题意，，，成等差数列，即，

当均为奇数时，，左边为偶数，故矛盾；

当均为偶数时，，左边为偶数，故矛盾；

当为偶数，奇数时，，左边为偶数，故矛盾；

当为奇数，偶数时，，即．（8分）

（2）设，，（）成等差数列，则，

即，

整理得，，

若，则，因为，所以只能为2或4，

所以只能为1或2；

（12分）

若，则，，

故矛盾，

综上，只能，，成等差数列或，，成等差数列，其中为奇数，

从而的最大值为3．（16分）

试题Ⅱ（附加题）

21．【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若

多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．

A．（几何证明选讲）

如图，已知△ABC的内角A的平分线交BC于点D，

交其外接圆于点E．

求证：

ABACADAE．

证明：

连结EC，易得∠B∠E，（2分）

由题意，∠BAD∠CAE，

所以△ABD∽△AEC，（6分）

所以ABACADAE．（10分）

B．（矩阵与变换）

求矩阵的特征值和特征向量．

矩阵的特征多项式为，（2分）

令，解得的特征值，．（4分）

将代入二元一次方程组

解得

所以矩阵的属于特征值0的一个特征向量为；

（7分）

同理，将代入①解得

所以矩阵的属于特征值1的一个特征向量为．（10分）

C．（极坐标与参数方程）

在极坐标系中，已知A（1，），B（9，），线段AB的垂直平分线l与极轴交于点C，求l的极坐标方程及△ABC的面积．

易得线段AB的中点坐标为（5，），（2分）

设点P（ρ，θ）为直线l上任意一点，

在直角三角形OMP中，ρcos（θ－）＝5，

所以，l的极坐标方程为ρcos（θ－）＝5，（6分）

令θ＝0，得ρ＝10，即C（10，0）．（8分）

所以，△ABC的面积为：

×

（9－1）×

10×

sin＝20．（10分）

D．（不等式选讲）

已知，，求证：

．

因为，，且，（当且仅当时“=”成立）

所以，①（4分）

又，（当且仅当时“=”成立）②（8分）

由①②得（当且仅当时“=”成立）．（10分）

【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文

字说明、证明过程或演算步骤．

22．如图，在正四棱柱中，，．

（1）若，求与平面所成角的正弦值；

（2）若二面角的大小为，求的值．

如图，以点为坐标原点，，，分别

为，，轴，建立空间直角坐标系，

（1）当时，，，，，

则，，，

设平面的法向量，

则由得，

不妨取，则，此时，（3分）

故，

所以与平面所成角的正弦值为；

（2）由得，，，

不妨取，则，

此时，（7分）

又平面的法向量，

解得．（10分）

23．设为给定的不小于3的正整数．数集，记数集的所有

元子集的所有元素的和为．

（1）求，；

（2）求．

（1）易得数集，

则，（2分）

数集的2元子集中，每个元素均出现次，

故，（4分）

（2）易得数集的元子集中，每个元素均出现次，

故，（6分）

所以

．（10分）