盟1617学年下学期七年级期初调研考试数学试题附答案Word文件下载.docx
《盟1617学年下学期七年级期初调研考试数学试题附答案Word文件下载.docx》由会员分享,可在线阅读,更多相关《盟1617学年下学期七年级期初调研考试数学试题附答案Word文件下载.docx(9页珍藏版)》请在冰豆网上搜索。
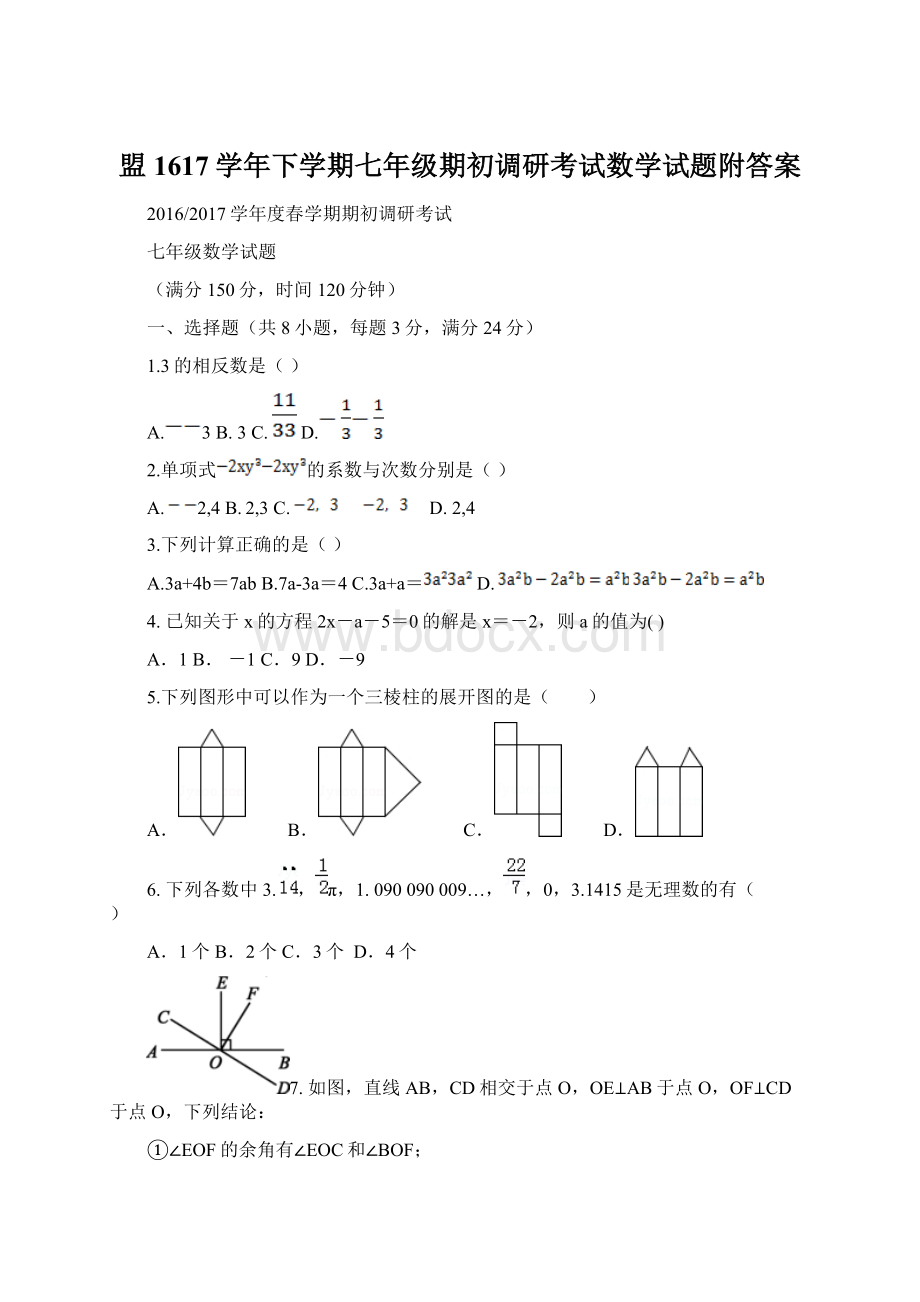
①∠EOF的余角有∠EOC和∠BOF;
②∠EOF=∠AOC=∠BOD;
③∠AOC与∠BOF互为余角;
④∠EOF与∠AOD互为补角.其中正确的个数是( )
A.1B.2C.3D.4
8.如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在哪条边上.()
A.ABB.BCC.CDD.DA
二、填空题(共10小题,每题3分,满分30分):
9.如果盈利25元记作+25元,那么亏损了30元记作___________
10.太阳的半径大约为696000千米,将696000用科学记数表示为_____.
11.已知方程2x-y=8,用含x的代数式表示y,则y=_____
12.已知:
如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=72°
,则∠BOD=_____.
13.若4a﹣2b=1,则3+8a﹣4b=_____.
14.如果将一根木条固定在墙上,至少需要两根钉子,这一事实依据_____.
15.按照如图所示的操作步骤,若输出的值为4,则输入的x值为_____.
16.如图,△ABC中,∠B=90°
,AB=5,BC=12,AC=13,点A到BC所在直线的距离是_____
17.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=80°
,∠BOC=40°
,则∠AOC等于_____.
18.如图,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度每秒,点B和C运动的速度是3个单位长度每秒.设三个点运动的时间为t秒(t≠5),设线段OA的中点为P,线段OB的中点为M,线段OC的中点为N,当2PM-PN=2时,t的值为_____.
三、解答题:
19.计算:
(每题4分,共8分)
(1)
(2)
20.解方程(组)(每题4分,共8分):
(1)
(2)
21.(10分)先化简,再求值:
已知:
A=3b2﹣2a2+5ab,B=4ab﹣2b2﹣a2
(1)化简:
2A﹣4B;
(2)当时,求2A﹣4B的值.
22.(10分)如图,这是6个棱长为1的正方体组成的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位);
(2)请在方格纸中用实线画出它的三个视图.
23.(8分)已知:
如图,线段AB=10,C是AB的中点.
(1)求线段BC的长;
(2)若点D在直线AB上,DB=2.5,求线段CD的长.
24.(8分)如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
25.(10分)某农户在荒坡上种植了杨树和松树,已知种植的杨树棵数比总数的一半多11棵,种植的松树棵数比总数的三分之一少2棵,两种树各种植了多少棵?
26.(10分)如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当点P运动几秒,S1=S,说明理由;
(3)请你探索是否存在某一时刻,使得S1=S2=S3?
若存在,求出t值;
若不存在,说明理由.
27.(12分)
【问题提出】已知∠AOB=70°
,∠AOD=∠AOC,∠BOD=3∠BOC(∠BOC<45°
),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=∠AOC,
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°
,∴α=14°
,∴∠BOC=14°
问:
当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】
(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:
∠BOC的度数分别是 .
28.(12分)如图,直线l上有AB两点,AB=18cm,点O是线段AB上的一点,OA=2OB
(1)OA=_____cm,OB=_____cm;
(2)若点C是直线AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为3cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P经过点O时,动点M从点O出发,以4cm/s的速度也向右运动.当点M追上点Q后立即返回,以4cm/s的速度向点P运动,遇到点P后再立即返回,以4cm/s的速度向点Q运动,如此往返.当点P与点Q重合时,P,Q两点停止运动.此时点M也停止运动.在此过程中,点M行驶的总路程是多少?
七年级数学参考答案
一选择题:
1.A2.A3.D4.D.5.A.6.B.7.D8.A
二、填空题;
9.-30元.10.6.96×
10511.y=2x-812.36°
13.514.两点确定一条直线.或过两点有且只有一条直线.
15.0或-616.517.40°
或80°
18.28/3或44/3
三.解答题
19.
(1)17
(2)1/6
20.
(1)x=1
(2)
21.
(1)14b2-6ab
(2)2A-4B=28
22.解:
(1)几何体的体积:
1×
6=6(立方单位),
表面积:
26(平方单位);
故答案为:
6,26;
(2)如图所示:
.
23.解:
(1)∵线段AB=10,C是AB的中点,∴BC=AB=5;
(2)如图1,∵BC=5,BD=2.5,∴CD=BC﹣CD=2.5;
如图2,∵BC=5,BD=2.5,∴CD=BC+CD=7.5,
综上所述:
线段CD的长为2.5或7.5.
24.解:
(1)∵两点之间线段最短,
∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.
(2)过H作HG⊥EF,垂足为G.
25.解:
设一共植了x棵树,由题意得
(x+11)+(x﹣2)=x,解得:
x=54,
x+11=38,x﹣2=16.
答:
种植杨树38棵,种植松树16棵.
26.解:
(1)由题意,得S3==8t.
8t;
(2)由题意,得
当0≤t≤4时,S1==16﹣4t,
当t>4时,S1==4t﹣16,
∴当16﹣4t=×
8×
时,t=2,
当4t﹣16=×
时,t=6.
当点P运动2秒或6秒时,S1=S;
(3)由题意,得16﹣4t=8t,解得:
t=.
当t=时,S1=S2=S3.
27.解:
(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,
如图2:
∠COD=∠BOD﹣∠BOC=2α,∵∠AOD=∠AOC,
∴∠AOD=∠COD=,∴∠AOB=∠BOD﹣∠AOD=3α﹣==70°
,
∴α=30°
.∴∠BOC=30°
;
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<45°
,∠AOD=∠AOC,∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,
则∠COD=∠BOC+∠COD=4α,∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°
∴α=10°
,∴∠BOC=10°
②若射线OD在∠AOB外部,如图4,
则∠COD=∠BOC+∠BOD=4α,∵∠AOD=∠AOC,∴∠AOD=∠COD=α,
∴∠AOB=∠BOD﹣∠AOD=3α﹣==70°
,∴α=42°
,∴∠BOC=42°
∠BOC的度数分别是14°
,30°
,10°
,42°
28.解:
(1)∵AB=18cm,OA=2OB,∴OA+OB=3OB=AB=18cm,解得OB=6cm,
OA=2OB=12cm.故答案为:
12,6;
(2)设CO的长是xcm,依题意有
①当点C在线段AB上时12﹣x=x+6+x,解得x=2.
②当点C在线段AB的延长线上时12+x=x+x-6解得x=18
故CO的长为2或18cm;
(3)①当0≤t<4时,依题意有2(12﹣3t)﹣(6+t)=4,解得t=2;
当4≤t<6时,依题意有2(3t﹣12)﹣(6+t)=4,解得t=34/5或t=6.8(不合题意舍去);
当6≤t≤9时,依题意有2(3t﹣12)﹣(6+t)=4,解得t=34/5或t=6.8
故当t为2s或6.8s时,2OP﹣OQ=4;
②20(cm).