学年九年级数学上学期期中试题 青岛版IdocWord格式.docx

学年九年级数学上学期期中试题 青岛版IdocWord格式.docx

《学年九年级数学上学期期中试题 青岛版IdocWord格式.docx》由会员分享，可在线阅读，更多相关《学年九年级数学上学期期中试题 青岛版IdocWord格式.docx（12页珍藏版）》请在冰豆网上搜索。

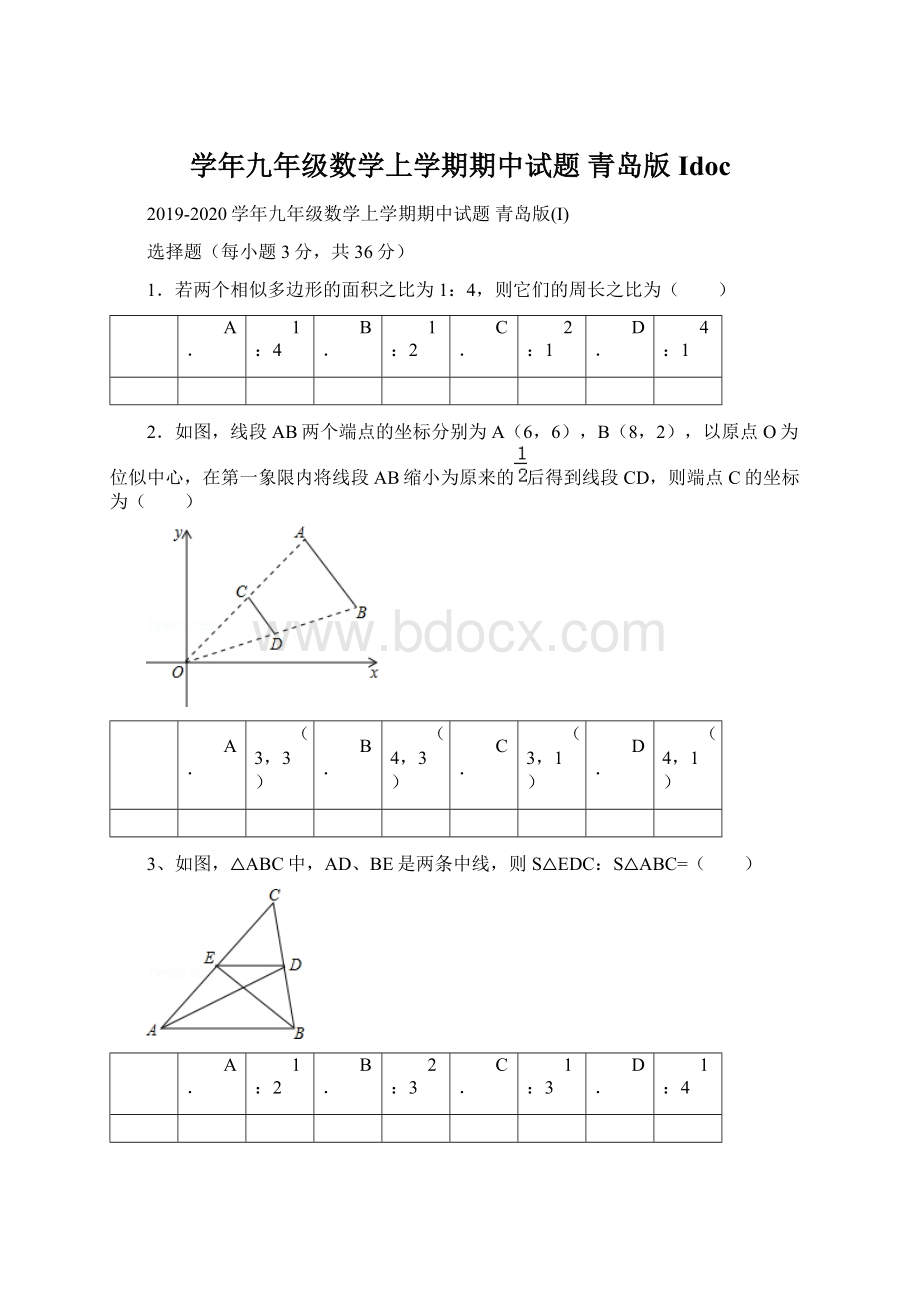
（4，3）

（3，1）

（4，1）

3、如图，△ABC中，AD、BE是两条中线，则S△EDC：

S△ABC=（　　）

3

4.如图，已知△ABC和△ADE均为等边三角形，D在BC上，DE与AC相交于点F，AB=9，BD=3，则CF等于（　　）

5.如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（　　）

6．在△ABC中，若|cosA﹣|+（1﹣tanB）2=0，则∠C的度数是（　　）

45°

60°

75°

105°

7.如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：

2，则斜坡AB的长为（　　）

4米

6米

12米

24米

8.从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°

，看到楼顶部点D处的仰角为60°

，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（　　）

（6+6）米

（6+3）米

（6+2）米

9.如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°

，则∠AOC的大小是（　　）

30°

70°

10.如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（　　）

1或5

5

11.如图，⊙O的直径AB=2，弦AC=1，点D在⊙O上，则∠D的度数是（　　）

12.如图，在半径为6cm的⊙O中，点A是劣弧的中点，点D是优弧上一点，且∠D=30°

，下列四个结论：

①OA⊥BC；

②BC=6；

③sin∠AOB=；

④四边形ABOC是菱形．

其中正确结论的序号是（　　）

①③

①②③④

②③④

①③④

二、填空题（每小题3分，共18分）

13.已知△ABC∽△DEF，其中AB=5，BC=6，CA=9，DE=3，那么△DEF的周长是　　．

14.如图，在△ABC中，两条中线BE、CD相交于点O，则S△DOE：

S△COB=_______

15.如图，在△ABC中，∠A=30°

，∠B=45°

，AC=，则AB的长为　　．

16.在Rt△ABC中，∠C=90°

，sinA=，则tanB的值为_______

17.如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2cm，∠BCD=22°

30′，则⊙O的半径为　　cm．

18.如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为　　cm．

三．解答题

19．计算：

（每小题6分，共12分）

（1）、sin45-++6tan30

（2）、sin30-cos45.tan60+

20．（12分）

如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）．

（1）画出△ABC关于y轴对称的图形△A1B1C1，并直接写出C1点坐标；

（2）以原点O为位似中心，位似比为1：

2，在y轴的左侧，画出△ABC放大后的图形△A2B2C2，并直接写出C2点坐标；

（3）如果点D（a，b）在线段AB上，请直接写出经过

（2）的变化后点D的对应点D2的坐标．

21．（10分）

如图，△ABC中，AD⊥BC，垂足是D，若BC=14，AD=12，tan∠BAD=，求sinC的值．

22．（10分）如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；

从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，求建筑物的高．

23．（10分）

小明去爬山，在山脚看山顶角度为30°

，小明在坡比为5：

12的山坡上走1300米，此时小明看山顶的角度为60°

，求山高。

24．（12分）如图，四边形ABCD是平行四边形，以对角线BD为直径作⊙O，分别与BC，AD相交于点E，F．

（1）求证：

四边形BEDF为矩形；

（2）BD2=BE•BC，试判断直线CD与⊙O的位置关系，并说明理由．

答案卡

考号：

_____

一选择题

1.______2______3_______4_______5________6________7________8________9________

10_______11________12________

二、填空题

13__________14________15_________16___________17____________18____________

答案

1、B2A．3D．4B5D6C7.B8.A9.C10.B11C12B

13、1214、1：

415、3+16、17、218、2

19．

（1）1—

（2）—

20．解：

（1）如图所示：

△A1B1C1，即为所求，

C1点坐标为：

（3，2）；

（2）如图所示：

△A2B2C2，即为所求，

C2点坐标为：

（﹣6，4）；

（3）如果点D（a，b）在线段AB上，经过

（2）的变化后D的对应点D2的坐标为：

（2a，2b）．

21．

解：

∵在直角△ABD中，tan∠BAD==，

∴BD=AD•tan∠BAD=12×

=9，

∴CD=BC﹣BD=14﹣9=5，

∴AC===13，

∴sinC==．

22．解：

∵AB⊥BH，CD⊥BH，EF⊥BH，

∴AB∥CD∥EF，

∴△CDG∽△ABG，△EFH∽△ABH，

∴=，=，

∵CD=DG=EF=2m，DF=52m，FH=4m，

∴=，

=，

解得BD=52m，

解得AB=54m．

23．解：

∵BE：

AE=5：

12，

=13，

∴BE：

AE：

AB=5：

12：

13，

∵AB=1300米，

∴AE=1200米，

BE=500米，

设EC=x米，

∵∠DBF=60°

，

∴DF=x米．

又∵∠DAC=30°

∴AC=CD．

即：

1200+x=（500+x），

解得x=600﹣250．

∴DF=x=600﹣750，

∴CD=DF+CF=600﹣250（米）．

答：

山高CD为（600﹣250）米．

24．

（1）证明：

连接OD，

∵AC是直径，∠ACB=90°

∴BC是⊙O的切线，∠BCA=90°

．

又∵DE是⊙O的切线，

∴ED=EC，∠ODE=90°

∴∠ODA+∠EDB=90°

∵OA=OD，∴∠OAD=∠ODA，

又∵∠OAD+∠DBE=90°

∴∠EDB=∠EBD，

∴ED=EB，

∴EB=EC．

（2）解：

当以点O、D、E、C为顶点的四边形是正方形时，则∠DEB=90°

又∵ED=EB，

∴△DEB是等腰直角三角形，则∠B=45°

∴△ABC是等腰直角三角形．