运筹学作业文档格式.docx

运筹学作业文档格式.docx

《运筹学作业文档格式.docx》由会员分享，可在线阅读，更多相关《运筹学作业文档格式.docx（22页珍藏版）》请在冰豆网上搜索。

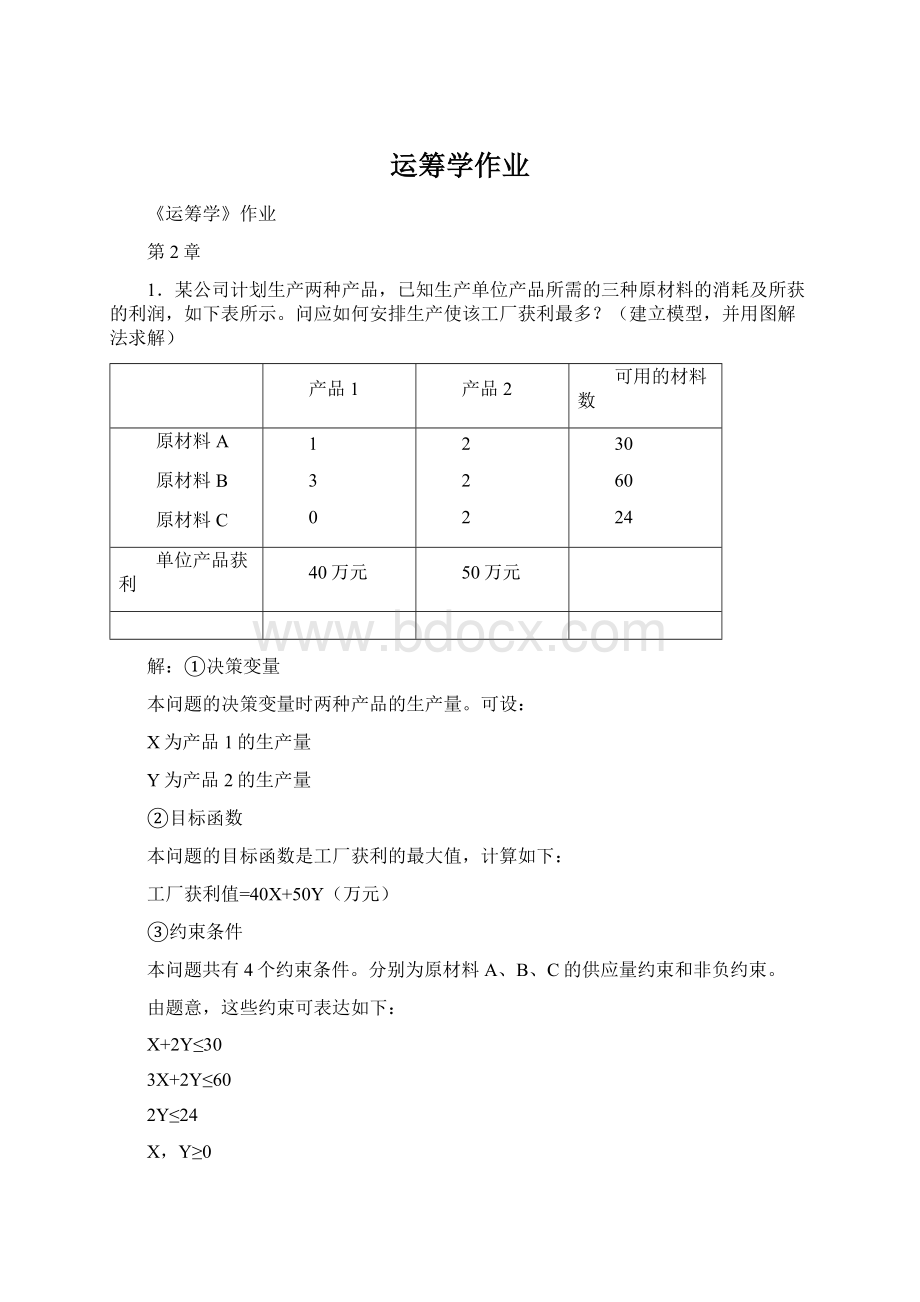
①决策变量

本问题的决策变量时两种产品的生产量。

可设：

X为产品1的生产量

Y为产品2的生产量

②目标函数

本问题的目标函数是工厂获利的最大值，计算如下：

工厂获利值=40X+50Y（万元）

③约束条件

本问题共有4个约束条件。

分别为原材料A、B、C的供应量约束和非负约束。

由题意，这些约束可表达如下：

X+2Y≤30

3X+2Y≤60

2Y≤24

X，Y≥0

由上述分析，可建立该最大化问题的线性规划模型如下：

o.b.Max40X+50Y

s.t.X+2Y≤30（原材料A的使用量约束）①

3X+2Y≤60（原材料B的使用量约束）②

2Y≤24（原材料C的使用量约束）③

X≥0，Y≥0（非负约束）④

建立excel模型

单位产品需求量

40

50

模型

决策变量

产量

15

7.5

工厂获利

975

约束

使用量（左边）

可提供量（右边）

<

=

作图法：

见下图:

X+2Y=30（原材料A的使用量约束）①

3X+2Y=60（原材料B的使用量约束）②

2Y=24（原材料C的使用量约束）③

40X+50Y=975⑤

作40X+50Y=0的平行线得到①②的交点为最大值

即产品1为15产品2为7.5时工厂获利最大为975

2．某公司计划生产两种产品，已知生产单位产品所需的两种原材料的消耗和人员需要及所获的利润，如下表所示。

人时

4

12

300万元

500万元

本问题的目标函数是工厂获利的最大值，课计算如下：

工厂获利值=300X+500Y（万元）

X≤4

2Y≤12

3X+2Y≤24

o.b.Max300X+500Y

s.t.X≤4（原材料A的使用量约束）①

2Y≤12（原材料B的使用量约束）②

3X+2Y≤24（原材料C的使用量约束）③

X≥0，Y≥0（非负约束）④

300

500

6

4200

作图法见下图

X=4（原材料A的使用量约束）①

2Y=12（原材料B的使用量约束）②

3X+2Y=24（原材料C的使用量约束）③

300X+500Y=4200⑤

作300X+500Y=0的平行线①②③得到在的交点处最大值

即产品1为4产品2为6时工厂获利最大为4200

3.下表是一个线性规划模型的敏感性报告，根据其结果，回答下列问题：

1）是否愿意付出11元的加班费，让工人加班；

2）如果工人的劳动时间变为402小时，日利润怎样变化？

3）如果第二种家具的单位利润增加5元，生产计划如何变化？

MicrosoftExcel9.0敏感性报告

工作表[ex2-6.xls]Sheet1

报告的建立:

2001-8-611:

04:

02

可变单元格

终

递减

目标式

允许的

单元格

名字

值

成本

系数

增量

减量

$B$15

日产量（件）

100

20

1E+30

$C$15

80

10

2.5

$D$15

日产量（件）

5.0

$E$15

-2.0

2.0

阴影

价格

限制值

$G$6

劳动时间（小时/件）

400

8

25

$G$7

木材（单位/件）

600

200

$G$8

玻璃（单位/件）

800

1000

在不影响生产计划的情况下劳动时间的范围[300，425]，此时劳动时间增加1小时，利润增加8*1=8元。

即工人加班产生的利润为8元/小时，则如果付11元的加班费产生的利润为8-11=-3元/小时。

利润减少。

则不愿意付11元的加班费，让工人加班。

2）如果第二种家具的单位利润增加5元，生产计划如何变化？

第二种家具的单位利润增加5元，则利润为25元，在第二种家具的允许范围[17.5.，30]内，则生产计划不会变化。

利润增加量为：

80*5=400元

4某公司计划生产两种产品，已知生产单位产品所需的三种原材料的消耗及所获的利润，如下表所示。

（建立模型，并用图解法求解）（20分）

0.6

0.4

0.5

0.1

12000

4000

6000

25元

10元

工厂获利值=25X+10Y（元）

0.6X+0.5Y≤12000

0.4X+0.1Y≤4000

0.4Y≤6000

o.b.Max25X+10Y

s.t.0.6X+0.5Y≤12000①

0.4X+0.1Y≤4000②

0.4Y≤6000③

6250

15000

306250

11250

见下图

0.6X+0.5Y=12000①

0.4X+0.1Y=4000②

0.4Y=6000③

25X+10Y=306250⑤

作25X+10Y=0的平行线得到②③的交点为最大值

即产品1为6250产品2为15000时工厂获利最大为306250

5.线性规划的解有唯一最优解、无穷多最优解、无界解和无可行解四种。

6.在求运费最少的调度运输问题中，如果某一非基变量的检验数为4，则说明如果在该空格中增加一个运量，运费将增加4。

7.“如果线性规划的原问题存在可行解，则其对偶问题一定存在可行解”，这句话对还是错？

错

第3章

1．一公司开发出一种新产品，希望通过广告推向市场。

它准备用电视、报刊两种广告形式。

这两种广告的情况见下表。

要求至少30万人看到广告，要求电视广告数不少于8个，至少16万人看到电视广告。

应如何选择广告组合，使总费用最小（建立好模型即可，不用求解）。

媒体

可达消费者数

单位广告成本

媒体可提供的广告数

电视

2.3

1500

报刊

1.5

450

本问题的决策变量是选择两种媒体的数量。

X为选择电视的数量

Y为选择报刊的数量

本问题的目标函数是总费用的最小值，课计算如下：

总费用=1500X+450Y

2.3X+1.5Y≥30

X≥8

X≤15

Y≤25

2.3X≥16

s.t.2.3X+1.5Y≥30

7.733333

总费用最小值

15480

电视可提供数

报刊可提供数

电视广告达到