燕山大学里仁学院运筹学考题附答案Word下载.docx
《燕山大学里仁学院运筹学考题附答案Word下载.docx》由会员分享,可在线阅读,更多相关《燕山大学里仁学院运筹学考题附答案Word下载.docx(13页珍藏版)》请在冰豆网上搜索。
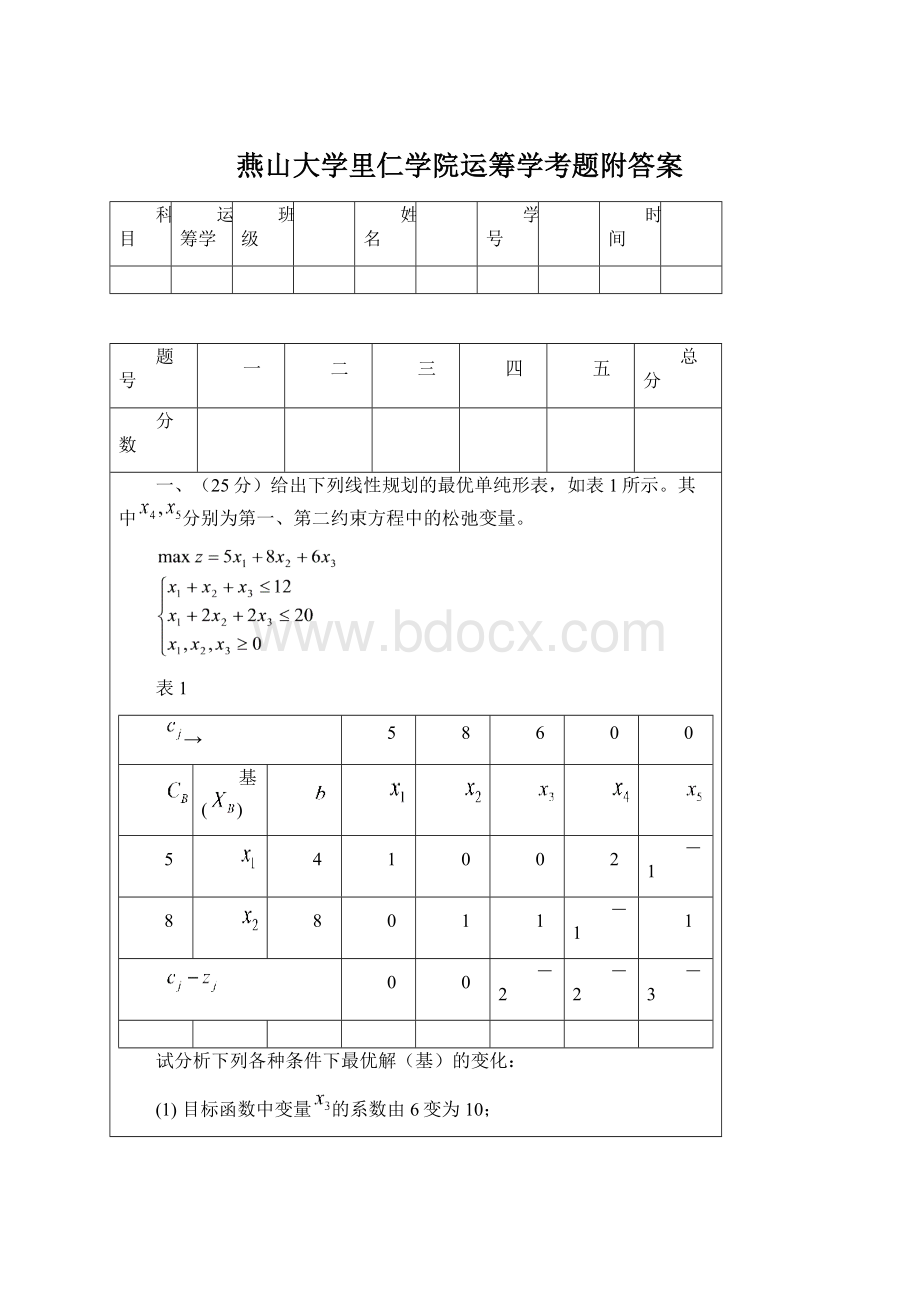
一、(25分)给出下列线性规划的最优单纯形表,如表1所示。
其中分别为第一、第二约束方程中的松弛变量。
表1
→
5
8
6
基()
4
1
2
-1
-2
-3
试分析下列各种条件下最优解(基)的变化:
(1)目标函数中变量的系数由6变为10;
(2)约束条件右端项由变为;
(3)在原线性规划的约束条件上,增加约束条件:
。
其最优解是否变化?
如变化,求出最优解。
二、(25分)表2中给出了一个运输问题,回答下列问题:
1、求解运输问题的初始基可行解的方法有哪几种,都是什么?
2、对于已经求得的初始可行解进行最优性检验有几种方法,都是什么?
运输规划的基可行解最优的条件是什么?
3、利用最小元素法求下列运输问题的初始基可行解,并检验该初始基可行解的最优性。
表2
销地
产地
产量
3
7
11
9
10
销量
三、(20分)用Gomory割平面法求解如下整数规划问题,已知该整数规划的松弛问题的最优单纯形表如表3,其中分别为第一、第二约束方程中的松弛变量。
表3
CB
XB
b
3/4
-1/4
1/4
7/4
-1/2
v4
v2
四、(10分)应用Dijkstra算法求图1中的网络从到的最短路径(只需在图上标号并指出最短路径)。
v1
v6
图1
五、(20分)
图2
要求:
(1)用图上计算法计算图2中各事项的时间参数,各工作的时间参数以及时差;
(2)指出该网络图的关键路径。
试题答案
解:
(1)题意即为由6变为10,此时最优单纯形表1变为下表:
【1】
这时原方案已不再是最优方案,再经过一次迭代,得到最终单纯形表:
-5
由最终单纯形表可得,此时最优解变为:
,目标函数最优值变为:
(2)题意即为由12变为30,此时最优单纯形表1中的列向量将变为:
最终单纯形表由表1变为下表:
(2分)
40
-10
【-1】
这时原方案已不是最优方案,用对偶单纯形法再迭代一次,得到最终单纯形表:
20
-4
(3)增加新约束条件:
后,原最优解不满足新约束条件,即16>
13不成立,故原最优解会发生变化。
(1分)
新约束加入松弛变量标准化:
,置于表1得下表:
13
将基变量,,所对应的列向量变为单位向量,经计算得下表
【-3】
再利用对偶单纯形法计算得下表:
(3分)
4/3
-1/3
2/3
1/3
-2/3
-10/3
-11/3
用对偶单纯形法求出新的最优解为:
,目标函数最优值变为:
1、答:
求解运输问题初始基可行解有三种方法:
最小元素法、西北角法和沃格尔法。
2、答:
初始基可行解的最优性检验有两种方法,它们是:
闭回路法以及位势法。
最优条件是所有检验数都非负。
3、解:
此问题是一个产销平衡问题,应用最小元素法求得的初始基可行解如下表:
下面应用闭回路法或位势法计算得各个空格的检验为:
此时还存在负检验数,该初始基可行解不是最优解,还需进一步改进。
由表3可知,此整数规划的松弛问题的最优解不是整数规划的解。
利用Gomory割平面法,将常数项都分解成整数和非负真分数之和,由于两个常数项具有相等的非负真分数部分,任从其中的一行,如第一行,产生割平面约束:
引入松弛变量,得割平面方程:
将这个新的约束条件反映到表3中,再用对偶单纯形法进行迭代得下表:
(
-3/4
【-3/4】
-4/3
由上表可得:
,已为整数解,且。
四、(10分)应用Dijkstra算法求图1中从到的最短路径(只需在图上标号并指出最短路径),。
用Dijkstra算法求解过程如下:
(每个顶点P标号正确得1分)
(1)首先给以P标号,给其余所有点T标号。
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
反向追踪得到的最短路径为:
。
(1)用图上计算法计算图2中各事项的时间参数,各工作的时间参数以及时差;
(1)用图上计算法(六时标注法)计算得图2中各事项的时间参数,各工作的时间参数以及时差如下图所示:
Ⅰ.各事项的时间参数:
事项①→⑦:
最早时间:
0最迟时间:
22
35
55
911
1111
1818
Ⅱ.各工作的时间参数及时差的六时标表示方法如下图所示:
其中六时标表示法为如下形式:
tES
tEF
R(i,j)
tLS
tLF
r(i,j)
(2)该网络图的关键路径为:
①→②→④→⑥→⑦。