北京各区初三几何压轴题汇总WORD版Word下载.docx

北京各区初三几何压轴题汇总WORD版Word下载.docx

《北京各区初三几何压轴题汇总WORD版Word下载.docx》由会员分享，可在线阅读，更多相关《北京各区初三几何压轴题汇总WORD版Word下载.docx（6页珍藏版）》请在冰豆网上搜索。

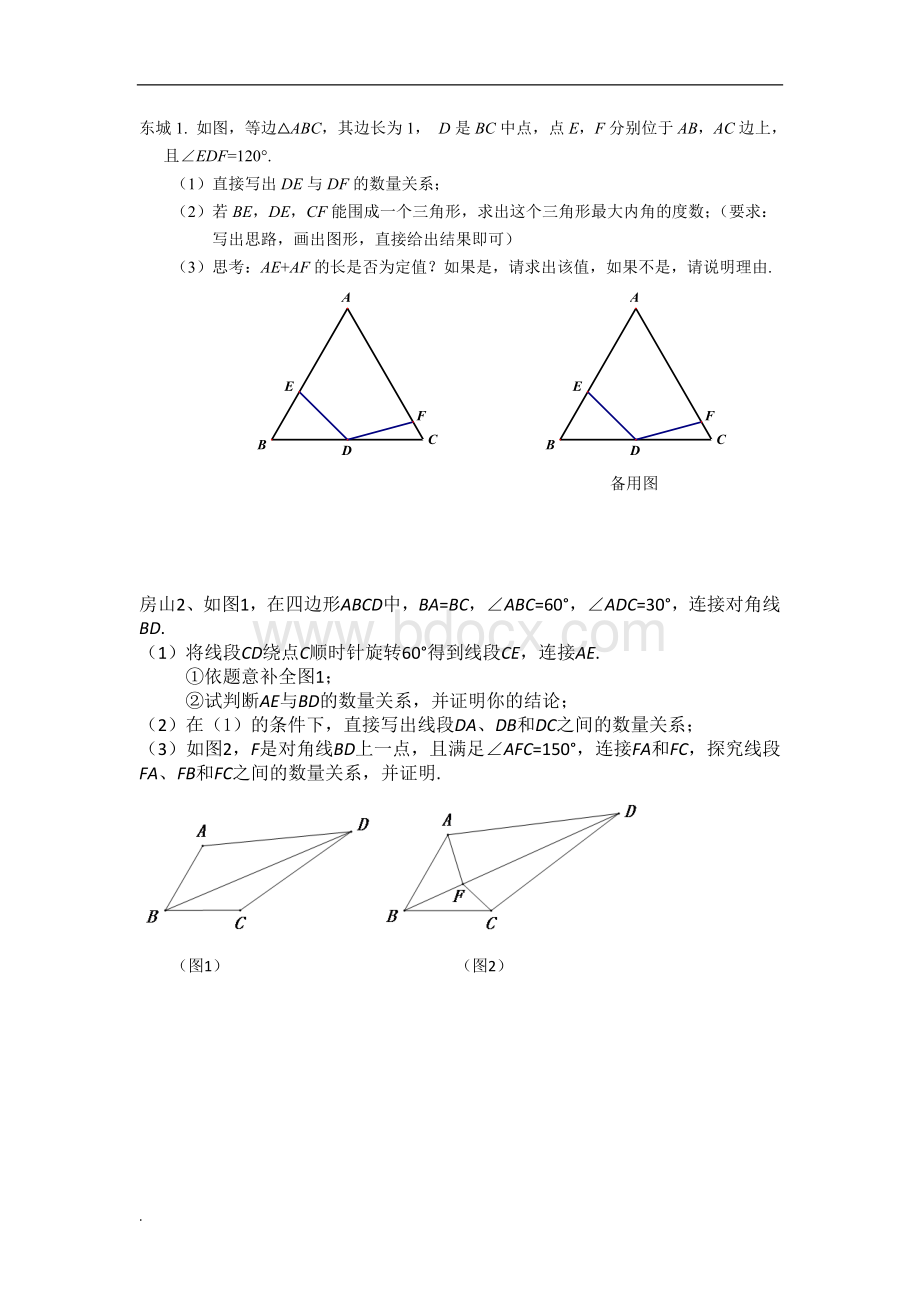
房山2、如图1，在四边形ABCD中，BA=BC，∠ABC=60°

，∠ADC=30°

，连接对角线BD.

（1）将线段CD绕点C顺时针旋转60°

得到线段CE，连接AE.

①依题意补全图1；

②试判断AE与BD的数量关系，并证明你的结论；

（2）在

（1）的条件下，直接写出线段DA、DB和DC之间的数量关系；

（3）如图2，F是对角线BD上一点，且满足∠AFC=150°

，连接FA和FC，探究线段FA、FB和FC之间的数量关系，并证明.

（图1）（图2）

海淀3．在△ABC中，AB=AC，∠BAC=，点D在射线BC上（与B、C两点不重合），以

AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．

（1）若点D在线段BC上，如图1.

②判断BC与CG的数量关系与位置关系，并加以证明；

（2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB=，则GE的

长为_______，并简述求GE长的思路．

图1备用图

怀柔4.在正方形ABCD中，点H在对角线BD上（与点B、D不重合），连接AH，将HA绕点H顺时针旋转90º

与边CD（或CD延长线）交于点P，作HQ⊥BD交射线DC于点Q.

（1）如图1:

②判断DP与CQ的数量关系并加以证明；

（2）若正方形ABCD的边长为，当DP=1时,试求∠PHQ的度数.

28题备用图

28题图1

门头沟5．在正方形ABCD中，连接BD．

（1）如图1，AE⊥BD于E．直接写出∠BAE的度数．

（2）如图1，在

（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°

后得到△AB'

E'

，AB'

与BD交于M，AE'

的延长线与BD交于N．

①依题意补全图1；

②用等式表示线段BM、DN和MN之间的数量关系，并证明．

（3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）

图1图2

平谷6．如图，在△ABC中，∠ACB=90°

，AC=BC=CD，∠ACD=α，将线段CD绕点C顺时针旋转90°

得到线段CE，连接DE，AE，BD．

（1）依题意补全图1；

（2）判断AE与BD的数量关系与位置关系并加以证明；

（3）若0°

＜α≤64°

，AB=4，AE与BD相交于点G，求点G到直线AB的距离的最大值．请写出求解的思路（可以不写出计算结果）．

图1

石景山7．在正方形ABCD中，E为边CD上一点，连接BE．

（1）请你在图1画出△BEM，使得△BEM与△BEC关于直线BE对称；

（2）若边AD上存在一点F，使得AF+CE=EF，请你在图2中探究∠ABF与[来源:

Z*xx*k.Com]

∠CBE的数量关系并证明；

（3）在

（2）的条件下，若点E为边CD的三等分点，且CE<

DE，请写出求

cos∠FED的思路．（可以不写出计算结果）．

图1图2备用图

顺义8．已知：

在△ABC中，∠BAC=60°

．

（1）如图1，若AB=AC，点P在△ABC内，且∠APC=150°

，PA=3，PC=4，把△APC绕着点A顺时针旋转，使点C旋转到点B处，得到△ADB，连接DP

①依题意补全图1；

②直接写出PB的长；

（2）如图2，若AB=AC，点P在△ABC外，且PA=3，PB=5，PC=4，求∠APC的度数；

（3）如图3，若AB=2AC，点P在△ABC内，且PA=，PB=5，∠APC=120°

，请直接写出PC的长．

通州9．△ABC中，，，于点，于点.

（1）如图1，作的角平分线交于点，连接AF.求证：

；

（2）如图2，连接，点G与点D关于直线对称，连接、.

①依据题意补全图形；

②用等式表示线段、、之间的数量关系，并加以证明.

西城10．在正方形中，点是射线上一个动点，连接，，点，分别为，的中点，连接交于点．

（1）如图1，当点与点重合时，的形状是_____________________；

（2）当点在线段的延长线上时，如图2．

①依题意补全图2；

②判断的形状，并加以证明；

（3）点与点关于直线对称，且点在线段上，连接，若点恰好在直线上，正方形的边长为2，请写出求此时长的思路．（可以不写出计算结果）

图1图2图3

燕山11．在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连接AD，BD，CD，其中CD交直线AP于点E．设∠PAB＝，∠ACE＝，∠AEC＝．

图2

（1）依题意补全图1；

（2）若＝15°

，直接写出和的度数；

（3）如图2，若60°

<

120°

，

①判断，的数量关系并加以证明；

②请写出求大小的思路．（可以不写出计算结果）