九年级学业水平模拟数学试题 IWord文档下载推荐.docx

九年级学业水平模拟数学试题 IWord文档下载推荐.docx

《九年级学业水平模拟数学试题 IWord文档下载推荐.docx》由会员分享，可在线阅读，更多相关《九年级学业水平模拟数学试题 IWord文档下载推荐.docx（30页珍藏版）》请在冰豆网上搜索。

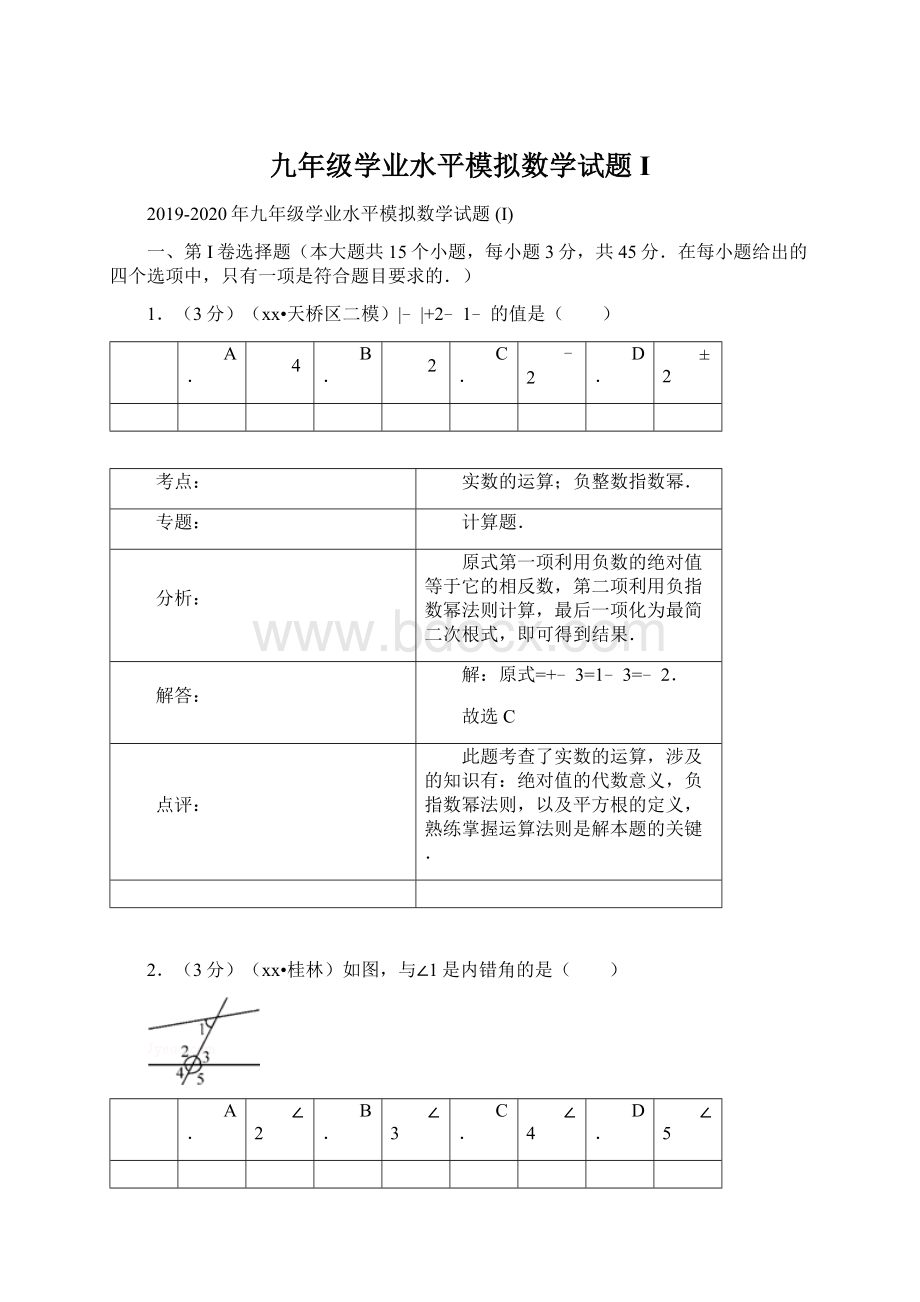
原式第一项利用负数的绝对值等于它的相反数，第二项利用负指数幂法则计算，最后一项化为最简二次根式，即可得到结果．

解答：

解：

原式=+﹣3=1﹣3=﹣2．

故选C

点评：

此题考查了实数的运算，涉及的知识有：

绝对值的代数意义，负指数幂法则，以及平方根的定义，熟练掌握运算法则是解本题的关键．

2．（3分）（xx•桂林）如图，与∠1是内错角的是（　　）

∠2

∠3

∠4

∠5

同位角、内错角、同旁内角．

根据内错角的定义找出即可．

根据内错角的定义，∠1的内错角是∠3．

故选B．

本题考查了“三线八角”问题，确定三线八角的关键是从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．

3．（3分）（xx•安徽）计算（2x）3÷

x的结果正确的是（　　）

8x2

6x2

8x3

6x3

整式的除法；

幂的乘方与积的乘方；

同底数幂的除法．

根据积的乘方等于各因式乘方的积和单项式的除法法则解答．

（2x）3÷

x=8x3÷

x=8x2．

故选A．

本题主要考查积的乘方的性质，单项式的除法，熟练掌握运算性质是解题的关键．

4．（3分）（xx•天桥区二模）为打造5A级景区，济南市组建了以趵突泉景区、大明湖景区为主体的“天下第一泉”风景区．清明节试运营期间景区共接待游客33.5万人，其中33.5万用科学记数法表示为（　　）

33.5×

104

0.335×

106

3.35×

105

科学记数法—表示较大的数．

科学记数法的表示形式为a×

10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当数绝对值＞10时，n是正数；

当原数的绝对值＜1时，n是负数．

33.5万=335000=3.35×

105．

故选D．

此题考查科学记数法的表示方法．科学记数法的表示形式为a×

10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

5．（3分）（xx•绥化）有理数a、b在数轴上的位置如图所示，则a+b的值（　　）

大于0

小于0

小于a

大于b

有理数的加法；

数轴．

数形结合．

根据图象可得a的绝对值小于b的绝对值，再根据a＜0，b＞0可得出a+b的取值情况．

由题意得：

a＜0，b＞0，且a的绝对值小于b的绝对值，

∴a+b＞0，且b＞a+b＞0，

本题考查有理数的加法，比较简单，关键是根据图形得出a和b的取值情况．

6．（3分）（xx•咸宁）不等式组的解集在数轴上表示为（　　）

在数轴上表示不等式的解集；

解一元一次不等式组．

分别求出各不等式的解集，并求出其公共解集，在数轴上表示出来即可．

，

由①得，x＞1；

由②得，x＜2，

故此不等式组的解集为：

1＜x≤2．

在数轴上表示为：

故选C．

本题考查的是在数轴上表示不等式的解集及解一元一次不等式组，熟知实心圆点与空心圆点的区别是解答此题的关键．

7．（3分）（xx•怀化）为了比较甲乙两种水稻秧苗是否出苗更整齐，每种秧苗各取10株分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙方差分别是3.9、15.8，则下列说法正确的是（　　）

甲秧苗出苗更整齐

乙秧苗出苗更整齐

甲、乙出苗一样整齐

无法确定

方差．

压轴题．

方差反映一组数据的波动大小，方差越大，波动性越大，反之也成立，即可得出答案．

∵甲、乙方差分别是3.9、15.8，

∴S2甲＜S2乙，

∴甲秧苗出苗更整齐；

本题考查方差的定义与意义：

一般地设n个数据，x1，x2，…xn的平均数为，方差S2=[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．

8．（3分）（xx•岳阳）如图，是由6个棱长为1个单位的正方体摆放而成的，将正方体A向右平移2个单位，向后平移1个单位后，所得几何体的视图（　　）

主视图改变，俯视图改变

主视图不变，俯视图不变

主视图不变，俯视图改变

主视图改变，俯视图不变

简单组合体的三视图．

主视图是从正面观察得到的图形，俯视图是从上面观察得到的图形，结合图形即可作出判断．

根据图形可得，图①及图②的主视图一样，俯视图不一样，即主视图不变，俯视图改变．

此题考查了简单组合体的三视图，掌握主视图及俯视图的观察方法是解答本题的关键，难度一般．

9．（3分）（xx•绍兴）化简，可得（　　）

分式的加减法．

先通分，然后进行同分母分式加减运算，最后要注意将结果化为最简分式．

==．

本题考查了分式的加减运算，题目比较容易．

10．（3分）（xx•天桥区二模）如图，⊙O是△ABC的外接圆，已知∠ABO=30°

，则∠ACB的大小为（　　）

60°

30°

45°

50°

圆周角定理．

首先根据等腰三角形的性质及三角形内角和定理求出∠AOB的度数，再利用圆周角与圆心角的关系求出∠ACB的度数．

△AOB中，OA=OB，∠ABO=30°

；

∴∠AOB=180°

﹣2∠ABO=120°

∴∠ACB=∠AOB=60°

此题主要考查了圆周角定理的应用，涉及到的知识点还有：

等腰三角形的性质以及三角形内角和定理．

11．（3分）（xx•天桥区二模）如图，平行四边形ABCD的对角线AC，BD相交于点O，点E是CD的中点，△ABD的周长为16cm，则△DOE的周长是（　　）

16cm

12cm

8cm

4cm

平行四边形的性质；

三角形中位线定理．

根据平行四边形的对边相等和对角线互相平分可得，BC=AD，DC=AB，DO=BO，E点是CD的中点，可得OE是△DCB的中位线，可得OE=BC．从而得到结果是8cm．

∵四边形ABCD是平行四边形，

∴O是BD中点，△ABD≌△CDB，

又∵E是CD中点，

∴OE是△BCD的中位线，

∴OE=BC，

即△DOE的周长=△BCD的周长，

∴△DOE的周长=△DAB的周长．

∴△DOE的周长=×

16=8cm．

本题主要考查平行四边形的性质及三角形中位线的性质的应用，是中考常见题型．

12．（3分）（xx•天桥区二模）如图，直线l的解析式为y=3x+3，若直线y=a与直线l的交点在第二象限，则a的取值范围是（　　）

1＜a＜2

3＜a＜4

﹣1＜a＜0

0＜a＜3

一次函数图象与系数的关系．

首先求出方程组的解，然后根据第二象限内点的坐标特征，列出关于a的不等式组，从而得出a的取值范围．

解方程组，

得．

∵交点在第二象限，

∴，

解得0＜a＜3．

本题主要考查了一次函数与方程组的关系及第二象限内点的坐标特征．两个一次函数图象的交点坐标就是对应的二元一次方程组的解，反之，二元一次方程组的解就是对应的两个一次函数图象的交点坐标．第二象限内点的坐标特征：

横坐标小于0，纵坐标大于0．

13．（3分）（xx•鄂州）直线y=﹣x﹣1与反比例函数（x＜0）的图象交于点A，与x轴相交于点B，过点B作x轴垂线交双曲线于点C，若AB=AC，则k的值为（　　）

﹣4

﹣6

﹣8

反比例函数与一次函数的交点问题．

计算题；

过A作AD⊥BC于D，先求出直线=﹣x﹣1与x轴交点B的坐标（﹣2，0），则得到C点的横坐标为﹣2，由于C点在反比例函数y=的图象上，可表示出C点坐标为（﹣2，﹣），利用等腰三角形的性质，由AC=AB，AD⊥BC，得到DC=DB，于是D点坐标为（﹣2，﹣），则可得到A点的纵坐标为﹣，利用点A在函数y=的图象上，可表示出点A的坐标为（﹣4，﹣），然后把A（﹣4，﹣）代入y=﹣x﹣1得到关于k的方程，解方程即可求出k的值．

过A作AD⊥BC于D，如图，

对于y=﹣x﹣1，令y=0，则﹣x﹣1=0，解得x=﹣2，

∴B点坐标为（﹣2，0），

∵CB⊥x轴，

∴C点的横坐标为﹣2，

对于y=，令x=﹣2，则y=﹣，

∴C点坐标为（﹣2，﹣），

∵AC=AB，AD⊥BC，

∴DC=DB，

∴D点坐标为（﹣2，﹣），

∴A点的纵坐标为﹣，

而点A在函数y=的图象上，

把y=﹣代入y=得x=﹣4，

∴点A的坐标为（﹣4，﹣），

把A（﹣4，﹣）代入y=﹣x﹣1得﹣=﹣×

（﹣4）﹣1，

∴k=﹣4．

本题考查了反比例函数与一次函数的交点问题：

反比例函数与一次函数的交点坐标满足两个函数的解析式．也考查了与x轴垂直的直线上所有点的横坐标相同以及等腰三角形的性质．

14．（3分）（xx•天桥区二模）在矩形ABCD的各边AB，BC，CD和DA上分别选取点E，F，G，H，使得AE=AH=CF=CG，如果AB=60，BC=40，四边形EFGH的最大面积是（　　）

1350

1300

1250

1200

二次函数的最值；

全等三角形的判定与性质；

矩形的性质．

设AE=AH=CF=CG=x，四边形EFGH的面积是S．分别求出矩形四个角落的三角形的面积