系统工程完整版本汪应洛主编课后题包括答案docxWord文档格式.docx
《系统工程完整版本汪应洛主编课后题包括答案docxWord文档格式.docx》由会员分享,可在线阅读,更多相关《系统工程完整版本汪应洛主编课后题包括答案docxWord文档格式.docx(23页珍藏版)》请在冰豆网上搜索。
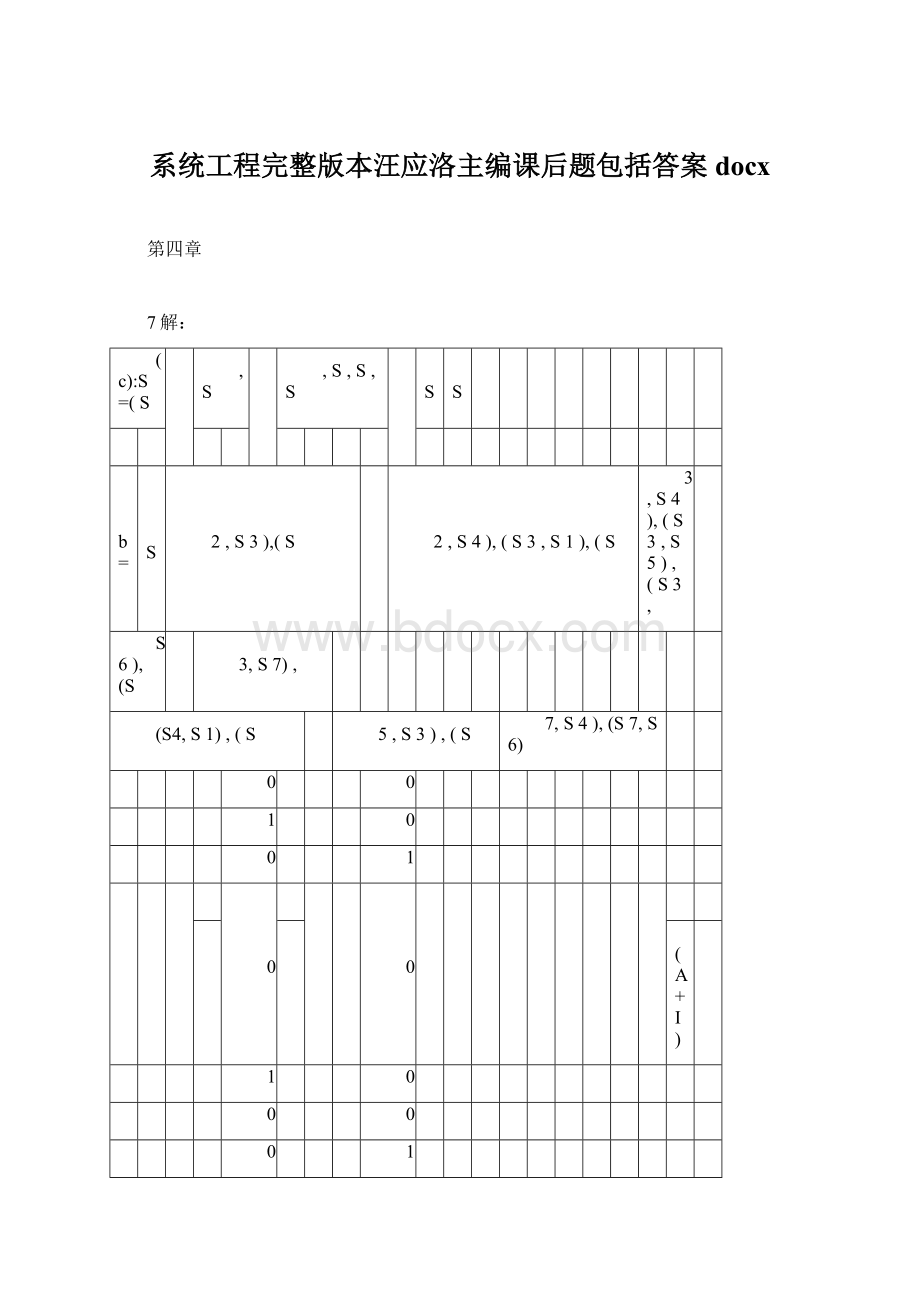
2,S4),(S3,S1),(S
3,S4),(S3,S5),(S3,
S6),(S
3,S7),
(S4,S1),(S
5,S3),(S
7,S4),(S7,S6)
A
M
=(A+I)
M'
8、根据下图建立系统的可达矩阵
V
P1
P2
P3
(A)
P4
(V)
P
P6
P7
P8
P9
100000011
010100011
101000011
000100011
解:
M100111011
000001011
111001111
000000011
000000001
9、
(2)解:
规范方法:
1、区域划分
SiR(Si)A(Si)C(Si)E(Si)B
(Si
8
1,2,4
1,3
1,2,3,4,5,2
6,7
1,2,3,4
2,4
1,2,3,4,5,4
2,4,5
5,6,7
2,4,5,6,7,6
2,4,5,7,8
6,7,8
因为B(S)={3,6}
所以设B中元素Bu=3、Bv=6
R(3)={1,2,3,4}、R(6)={2
,4,5,6,7,8}
R(3)∩R(6)={1
,2、3,4}∩{2
,4,5,6,7,8}
≠φ,故区域不可分解
2级位划分
Si
R(Si
A(Si)
C(Si)
C(Si)=
R(Si)
将满足C=R的元素2,8挑出作为第1级
将满足C=R的元素4挑出作为第2级
将满足C=R的元素1,5挑出作为第3级
将满足C=R的元素3,7挑出作为第4级
将满足C=R的元素6挑出作为第5级
将M按分级排列:
提取骨架矩阵如下:
A'
建立其递阶结构模型如下:
28
15
(1)实用方法:
(2)
建立其递阶结构模型同上。
第五章
9、解:
MT
MHMCT
TT
TEC
STT
ME
ML
11、某城市服务网点的规模可用SD研究。
现给出描述该问题的DYNAMO方程及其变量说明。
要求:
(1)绘制相应的SD流(程)图(绘图时可不考虑仿真控制变量);
(2)说明其中的因果反馈回路及其性质。
LS·
K=S·
J+DT*NS·
JKNS=90
RNS·
KL=SD·
K*P·
K/(LENGTH-TIME·
K)
ASD·
K=SE-SP·
KCSE=2
ASP·
K=SR·
K/P·
KASR·
K=SX+S·
K
CSX=60
LP·
K=P·
J+ST*NP·
JKNP=100
RNP·
KL=I*P·
KCI=0.02
其中:
LENGTH为仿真终止时间、TIME为当前仿真时刻,均为仿真控制变量;
S为个体服务
网点数(个),NS为年新增个体服务网点数(个/年),SD为实际千人均服务网点与期望差(个
/千人),SE为期望的千人均网点数,SP为千人均网点数(个/千人),SX为非个体服务网点数(个),SR为该城市实际拥有的服务网点数(个),P为城市人口数(千人),NP为年新增人口数(千人/年),I为人口的年自然增长率。
(1)因果关系图:
年新增个体
NS
服务网点数
千人均服务
+
S
网点期望差
个体服务
网点数
SX非个体
SD
SE期望千人
-
(-)
均网点数
千人均
实际服务
流程图:
S(90)
P(100)
NP
I(0.02)
SR
I
SX(60)
SDSP
SE
(2)
第六章:
12、今有一项目建设决策评价问题,已经建立起层次结构和判断矩阵如下图、表所示,试用
层次分析法确定五个方案的优先顺序。
综合效益U
经济效益C1环境效益C2社会效益C3
方
案
m1
m2
C2
m4
C3
U
C1
C2
C
1/3
1/5
m
1/7
1/2
1/4
1/9
9