正方体截面Word文档下载推荐.docx

正方体截面Word文档下载推荐.docx

《正方体截面Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《正方体截面Word文档下载推荐.docx（9页珍藏版）》请在冰豆网上搜索。

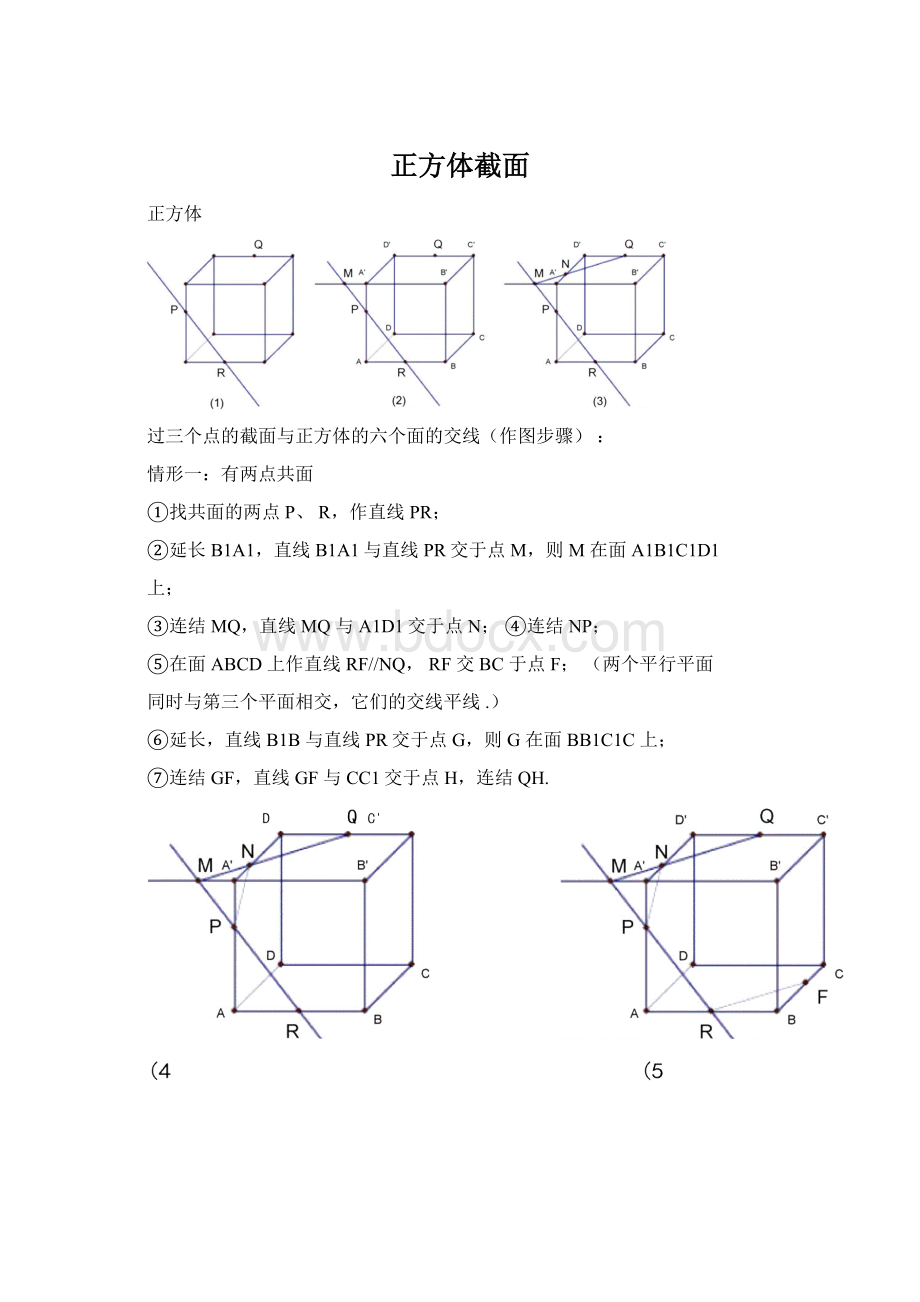
上；

③连结MQ，直线MQ与A1D1交于点N；

④连结NP；

⑤在面ABCD上作直线RF//NQ，RF交BC于点F；

（两个平行平面

同时与第三个平面相交，它们的交线平线.）

⑥延长，直线B1B与直线PR交于点G，则G在面BB1C1C上；

⑦连结GF，直线GF与CC1交于点H，连结QH.

情形二：

任两点不共面

①作直线PQ，则PQ为底面ABCD的斜线；

②过点Q做QQ1垂直CD于点Q1，则点Q在面ABCD上的射影为点

Q1，易知点P在面ABCD上的射影为点A；

③连结Q1A,直线Q1A与直线QP交于点M，则M为截面PQR上的

一点。

由观察可得，M、Q和R三点中有M、R共面，后面的步骤归

结为情形一（连结MR，⋯⋯）.

注意：

斜线在平面上的射影的确定方法有：

连结斜足和垂足，如图一；

连结两个垂足，

2

b

E

口

Haii^CMcronjioma;

u>

.

1.Dh=1（norcopcMeLlu^aropa）.

2.TpeyrojibHHKDEF-paBiio6e4peHHbiif（DEpaBHODF）.

aj2Qt+iy+】

qk=&

E）

\042,_网上+射+11

4.Seen=SADH；

=2上+I2（2+I）2

Bo3\（o;

KHbiesapnaHTbiotbciob（训1pa3Hbix3na4CHiifik）.

k=0nSeen.=2（paBHOCTopoHHMftdAjC|D）;

纪.厉

k=1=>

Scen.=8；

k=2=Seen.=18;

1/2Sпр=S（ACMN）=

S（ADC）—

S（MDN）=0,75*S（ADC）

=3/41·

/2AD*DC

/26·

=2,25.

译文：

Sсеч=Sпр/cosα（其中

Sсеч为截面面积，Sпр为投影面积，α为截

平面与底面ABCD之间的角）借助于横截面的对称性，我们所求的

投影只有一半的面积。

АСMN为MNLL1的投影。

1/2Sпр=S（ACMN）=S（ADC）—

S（MDN）=0,75*S（ADC）=3/41·

/2AD*DC=3/41·

那整个投影面积为Sпр=4,5。

在确定角α误认为它是∠OPK；

过KH⊥MN,则∠OHKα=，

KP=1/4BD=√13/4,KH=KPsin（∠KPH）=KPsin（2∠BDA）=√13/4*2*2/√13*3/√13=3/√13,tgα=OK/KH=√13/6cosα=1/√（1+tg2α）=6/7.

现在，我们终于求出Sсеч=Sпр/cosα=4,56÷

/7=63/12=21/4=5,25.