实验四:IIR数字滤波器设计及软件实现Word文件下载.doc
《实验四:IIR数字滤波器设计及软件实现Word文件下载.doc》由会员分享,可在线阅读,更多相关《实验四:IIR数字滤波器设计及软件实现Word文件下载.doc(9页珍藏版)》请在冰豆网上搜索。
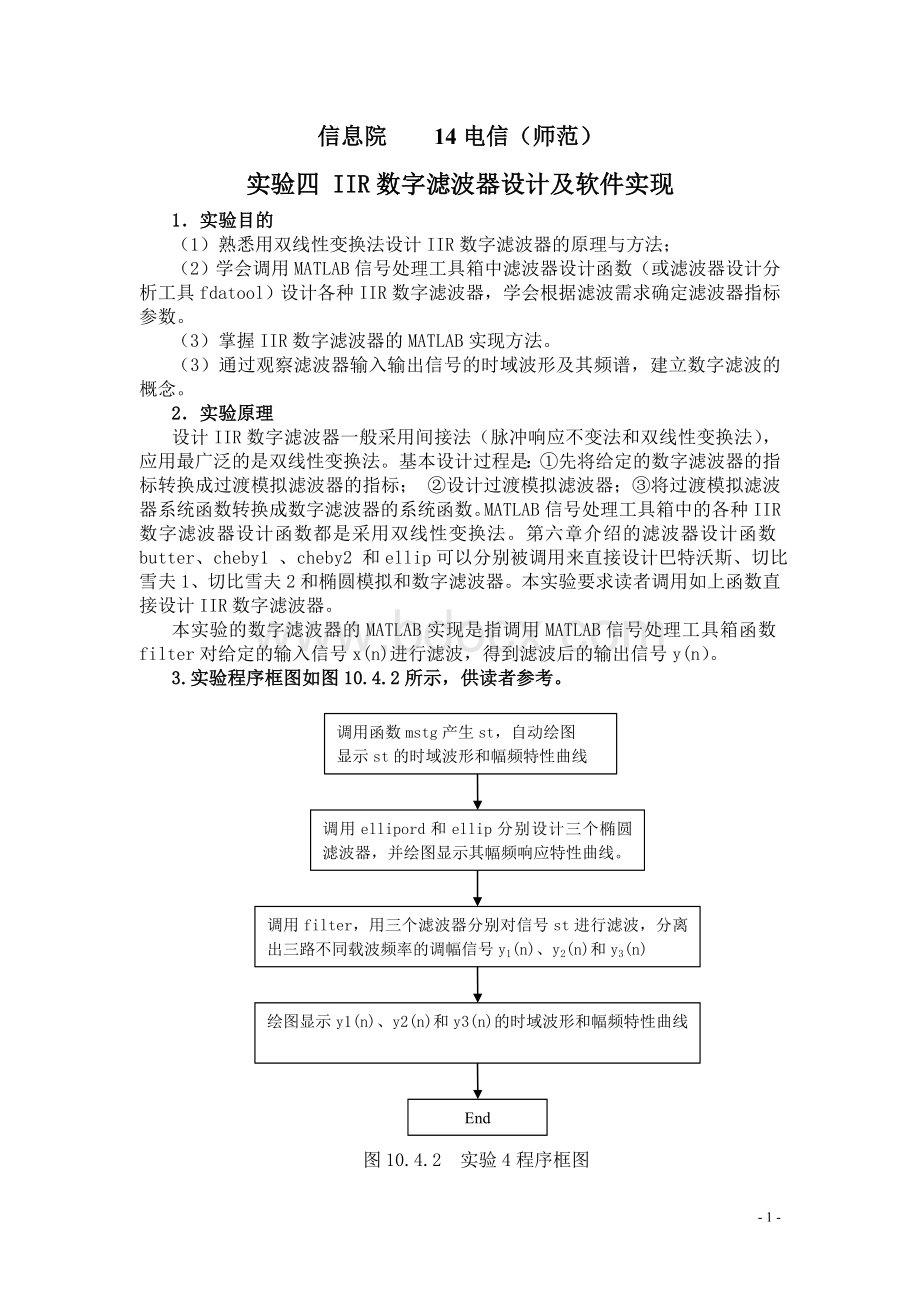
(1)调用信号产生函数mstg产生由三路抑制载波调幅信号相加构成的复合信号st,该函数还会自动绘图显示st的时域波形和幅频特性曲线,如图10.4.1所示。
由图可见,三路信号时域混叠无法在时域分离。
但频域是分离的,所以可以通过滤波的方法在频域分离,这就是本实验的目的。
图10.4.1三路调幅信号st的时域波形和幅频特性曲线
程序如下:
functionst=mstg
%²
ú
É
Ð
Å
º
ò
Á
Ï
¿
st,²
¢
Ô
Ê
¾
stµ
Ä
±
Ó
²
¨
Î
Í
Æ
µ
×
%st=mstg·
»
Ø
È
ý
Â
·
÷
ù
à
¼
³
ì
£
¬
¤
¶
N=800
N=800%NÎ
ª
¡
Fs=10000;
T=1/Fs;
Tp=N*T;
%²
Ñ
Fs=10kHz£
TpÎ
ä
t=0:
T:
(N-1)*T;
k=0:
N-1;
f=k/Tp;
fc1=Fs/10;
%µ
Ú
1Â
fc1=1000Hz,
fm1=fc1/10;
%µ
Ö
fm1=100Hz
fc2=Fs/20;
2Â
fc2=500Hz
fm2=fc2/10;
fm2=50Hz
fc3=Fs/40;
3Â
fc3=250Hz,
fm3=fc3/10;
fm3=25Hz
xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);
xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);
xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);
st=xt1+xt2+xt3;
%È
fxt=fft(st,N);
%¼
Ë
ã
%====Ò
æ
Ì
Ç
ß
====================
subplot(3,1,1)
plot(t,st);
grid;
xlabel('
t/s'
);
ylabel('
s(t)'
axis([0,Tp/8,min(st),max(st)]);
title('
(a)s(t)µ
'
)
subplot(3,1,2)
stem(f,abs(fxt)/max(abs(fxt)),'
.'
(b)s(t)µ
axis([0,Fs/5,0,1.2]);
f/Hz'
图形输出:
(2)要求将st中三路调幅信号分离,通过观察st的幅频特性曲线,分别确定可以分离st中三路抑制载波单频调幅信号的三个滤波器(低通滤波器、带通滤波器、高通滤波器)的通带截止频率和阻带截止频率。
要求滤波器的通带最大衰减为0.1dB,阻带最小衰减为60dB。
提示:
抑制载波单频调幅信号的数学表示式为
其中,称为载波,fc为载波频率,称为单频调制信号,f0为调制正弦波信号频率,且满足。
由上式可见,所谓抑制载波单频调幅信号,就是2个正弦信号相乘,它有2个频率成分:
和频和差频,这2个频率成分关于载波频率fc对称。
所以,1路抑制载波单频调幅信号的频谱图是关于载波频率fc对称的2根谱线,其中没有载频成分,故取名为抑制载波单频调幅信号。
容易看出,图10.4.1中三路调幅信号的载波频率分别为250Hz、500Hz、1000Hz。
如果调制信号m(t)具有带限连续频谱,无直流成分,则就是一般的抑制载波调幅信号。
其频谱图是关于载波频率fc对称的2个边带(上下边带),在专业课通信原理中称为双边带抑制载波(DSB-SC)调幅信号,简称双边带(DSB)信号。
如果调制信号m(t)有直流成分,则就是一般的双边带调幅信号。
其频谱图是关于载波频率fc对称的2个边带(上下边带),并包含载频成分。
答:
①对载波频率为250Hz的条幅信号,可以用低通滤波器分离,其指标为
带截止频率Hz,通带最大衰减dB;
阻带截止频率Hz,阻带最小衰减dB,
②对载波频率为500Hz的条幅信号,可以用带通滤波器分离,其指标为
带截止频率Hz,Hz,通带最大衰减dB;
阻带截止频率Hz,Hz,Hz,阻带最小衰减dB,
③对载波频率为1000Hz的条幅信号,可以用高通滤波器分离,其指标为
说明:
(1)为了使滤波器阶数尽可能低,每个滤波器的边界频率选择原则是尽量使滤波器过渡带宽尽可能宽。
(2)与信号产生函数mstg相同,采样频率Fs=10kHz。
(3)为了滤波器阶数最低,选用椭圆滤波器。
(3)编程序调用MATLAB滤波器设计函数ellipord和ellip分别设计这三个椭圆滤波器,并绘图显示其幅频响应特性曲线。
(4)调用滤波器实现函数filter,用三个滤波器分别对信号产生函数mstg产生的信号st进行滤波,分离出st中的三路不同载波频率的调幅信号y1(n)、y2(n)和y3(n),并绘图显示y1(n)、y2(n)和y3(n)的时域波形,观察分离效果。
(3)(4)程序如下:
%IIRÊ
è
°
í
þ
clearall;
%µ
Ã
¯
mstg²
Ò
¹
¸
´
st;
%
%µ
ë
st=mstg;
fp=280;
fs=450;
wp=2*fp/Fs;
ws=2*fs/Fs;
rp=0.1;
rs=60;
%DFÖ
ê
;
(µ
ø
½
ç
[N,wp0]=ellipord(wp,ws,rp,rs);
ellipod¼
DF½
Nº
wp
[B,A]=ellip(N,rp,rs,wp0);
ellip¼
DFÏ
Bº
A
y1t=filter(B,A,st);
%Â
%Ï
figure
(2);
subplot(2,1,1);
[H1,w]=freqz(B,A,1000);
m=abs(H1);
plot(w/pi,20*log(m/max(m)));
gridon;
ð
axis([0,1,-300,20]);
w/pi'
H1'
subplot(2,1,2);
ss=0:
0.02/800:
0.02-0.02/800;
plot(ss,y1t);
ó
axis([0,0.02,-1.2,1.2]);
y1t'
%N=1600;
%NÎ
%Fs=10000;
%t=0:
%figure(5)
%stem(k,abs(fft(y1t,1600))/max(abs(fft(y1t,1600))),'
%%´
fpl=450;
fpu=560;
fsl=275;
fsu=900;
wp=[2*fpl/Fs,2*fpu/Fs];
ws=[2*fsl/Fs,2*fsu/Fs];
rs=60;
y2t=filter(B,A,st);
figure(3);
[H2,w]=freqz(B,A,1000);
m=abs(H2);
H2'
plot(ss,y2t);
y2t'
%¸
fp=890;
fs=600;
[B,A]=ellip(N,rp,rs,wp0,'
high'
y3t=filter(B,A,st);
fi