立体几何大题练习题答案Word文件下载.doc

立体几何大题练习题答案Word文件下载.doc

《立体几何大题练习题答案Word文件下载.doc》由会员分享，可在线阅读，更多相关《立体几何大题练习题答案Word文件下载.doc（10页珍藏版）》请在冰豆网上搜索。

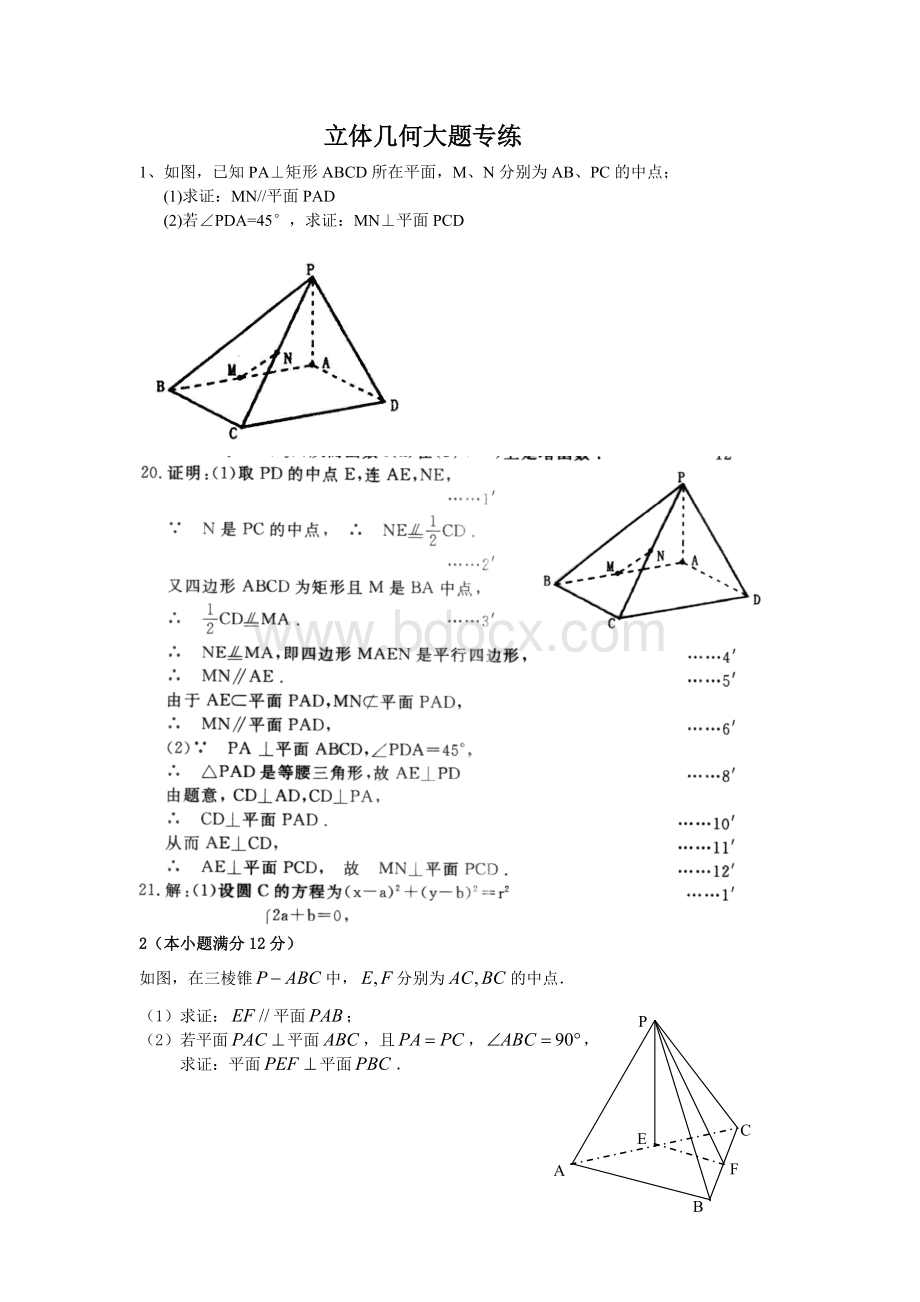
（2）若平面平面，且，，

求证：

平面平面．

（1）证明：

连结,、分别为、的中点，

.……………………2分

又平面，平面，

EF∥平面PAB.……………………5分

（2），为的中点，

……………………6分

又平面平面

面……………………8分

……………………9分

又因为为的中点，

……………………10分

面……………………11分

又面

面面……………………12分

3.如图，在直三棱柱ABC—A1B1C1中，AC=BC，点D是AB的中点。

BC1//平面CA1D；

（2）求证：

平面CA1D⊥平面AA1B1B。

4．已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是

　　AB、PC的中点．

（1）求证：

EF∥平面PAD；

（2）求证：

EF⊥CD；

　　（3）若∠PDA＝45°

，求EF与平面ABCD所成的角的大小．

5．（本小题满分12分）

如图，的中点．

；

6.如图，正方形所在的平面与三角形ＡDＥ所在平面互相垂直，△ＡＥＢ是等腰直角三角形，且ＡＥ＝ＥD　　　　　　　　　　　　设线段BC、的中点分别为F、，求证：

（1）∥；

（2）求二面角Ｅ－ＢＤ—Ａ的正切值．

取AD的中点N,连结FN,MN,则MN∥ED，FN∥CD

∴平面FMN∥平面ECD.

∵MF在平面FMN内,

∴FM∥平面ECD......5分

（2）连接EN,∵AE=ED，N为AD的中点，

∴EN⊥AD.

又∵面ADE⊥面ABCD，∴EN⊥面ABCD.

作NP⊥BD,连接EP,则EP⊥BD，

∴∠EPN即二面角E-BD-A的平面角，

设AD=a,∵ABCD为正方形，⊿ADE为等腰三角形，∴EN=a,NP=a.

∴tan∠EPN=.......10分

7.如图，一个圆锥的底面半径为2cm，高为6cm，其中有一个高为cm的内接圆柱.

（1）试用表示圆柱的侧面积；

（2）当为何值时，圆柱的侧面积最大.

19.

（1）解：

设所求的圆柱的底面半径为

则有,即.

∴.......5分

（2）由

（1）知当时，这个二次函数有最大值为

所以当圆柱的高为3cm时，它的侧面积最大为......10分

8．（10分）

如图，在三棱锥中，⊿是等边三角形，∠PAC=∠PBC=90º

.

AB⊥PC；

（2）若，且平面⊥平面，求三棱锥体积.

解：

（1）因为是等边三角形，,

所以,可得。

如图，取中点，连结,,

则,,

所以平面,

所以......5分

（2）作，垂足为，连结．

因为，

所以，．

由已知，平面平面，故．　　　　　　　　

因为，所以都是等腰直角三角形。

由已知，得，的面积．

因为平面，

所以三角锥的体积......10分

9.（本题满分12分）如图，在四棱锥P－ABCD中，底面ABCD为平行四边形，

∠ADC＝45°

，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．

（1）证明PB∥平面ACM；

（2）证明AD⊥平面PAC；

（3）求直线AM与平面ABCD所成角的正切值．

解析：

（1）证明：

如图，连接BD，MO，在平行四边形ABCD中，因为O为AC的中点，所以O为BD的中点．

又M为PD的中点，所以PB∥MO.因为PB⊄平面ACM，MO⊂平面ACM，所以PB∥平面ACM.

（2）证明：

因为∠ADC＝45°

，且AD＝AC＝1，所以∠DAC＝90°

，即AD⊥AC.又PO⊥平面ABCD，AD⊂平面ABCD，所以PO⊥AD.而AC∩PO＝O，所以AD⊥平面PAC.

（3）如图，取DO中点N，连接MN，AN.因为M为PD的中点，所以MN∥PO，且MN＝PO＝1，由PO⊥平面ABCD，得MN⊥平面ABCD，所以∠MAN是直线AM与平面ABCD所成的角．在Rt△DAO中，AD＝1，AO＝，

DO＝.从而AN＝DO＝.在Rt△ANM中，tan∠MAN＝＝＝，

即直线AM与平面ABCD所成角的正切值为.

10（本小题满分12分）

如图，在侧棱垂直于底面的三棱柱中，，，，，点是的中点．

（Ⅰ）求证：

（II）求证：

（III）求三棱锥的体积．

证明：

（Ⅰ）在△ABC中，∵，，，

∴△ABC为直角三角形，∴，……………1分

又∵平面ABC，∴，，……………2分

∴平面，∴．……………4分

（II）设与交于点E，则E为的中点，连结DE，……………5分

则在△中，，又，……………7分

∴平面．……………8分

（III）在△ABC中，过C作，F为垂足，∵平面平面ABC，

∴平面，而，……………9分

∵，……………10分

而，……………11分

∴．……………12分

11.（本小题满分12分）

如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB=AD,∠BAD=60°

E、F分别是AP、AD的中点

求下：

（Ⅰ）直线EF//平面PCD；

（Ⅱ）平面BEF⊥平面PAD.

12.（本小题满分12分）

如图所示，在四棱锥中，底面是正方形，侧棱底面是的中点，作交于点F。

（I）求证：

（II）求证：

（III）求二面角的大小。

13．（本小题满分12分）

如图，四棱锥中，底面是边长为2的正方形，

（1）求二面角的度数

（2）若是侧棱的中点，求异面直线与所成角的正切值

14．（本小题满分12分）

若图为一简单组合体，其底面ABCD为正方形，PD平面ABCD，EC//PD，且PD=2EC。

（1）求证：

BE//平面PDA；

（2）若N为线段PB的中点，求证：

EN平面PDB；

（1）证明：

EC∥PD∴EC∥面PAD；

同理BC∥面PAD；

∴面BEC∥面PAD；

∴BE∥面PAD

（2）证明：

取BD的中点O，连NO、CO，易知，CO⊥BD；

又∵CO⊥PD;

∴CO⊥面PBD。

15．（本小题满分12分）

如图，在多面体ABCDE中，底面为等腰直角三角形，且，侧面BCDE是菱形，O点是BC的中点，EO平面ABC。

（1）求异直线AC和BE所成角的大小；

（2）求平面ABE与平面ADE所成锐二面角的余弦值。