Hypothesis Testing Basics.docx

Hypothesis Testing Basics.docx

《Hypothesis Testing Basics.docx》由会员分享，可在线阅读，更多相关《Hypothesis Testing Basics.docx（14页珍藏版）》请在冰豆网上搜索。

HypothesisTestingBasics

HypothesisTestingBasics

TheNormalDistribution

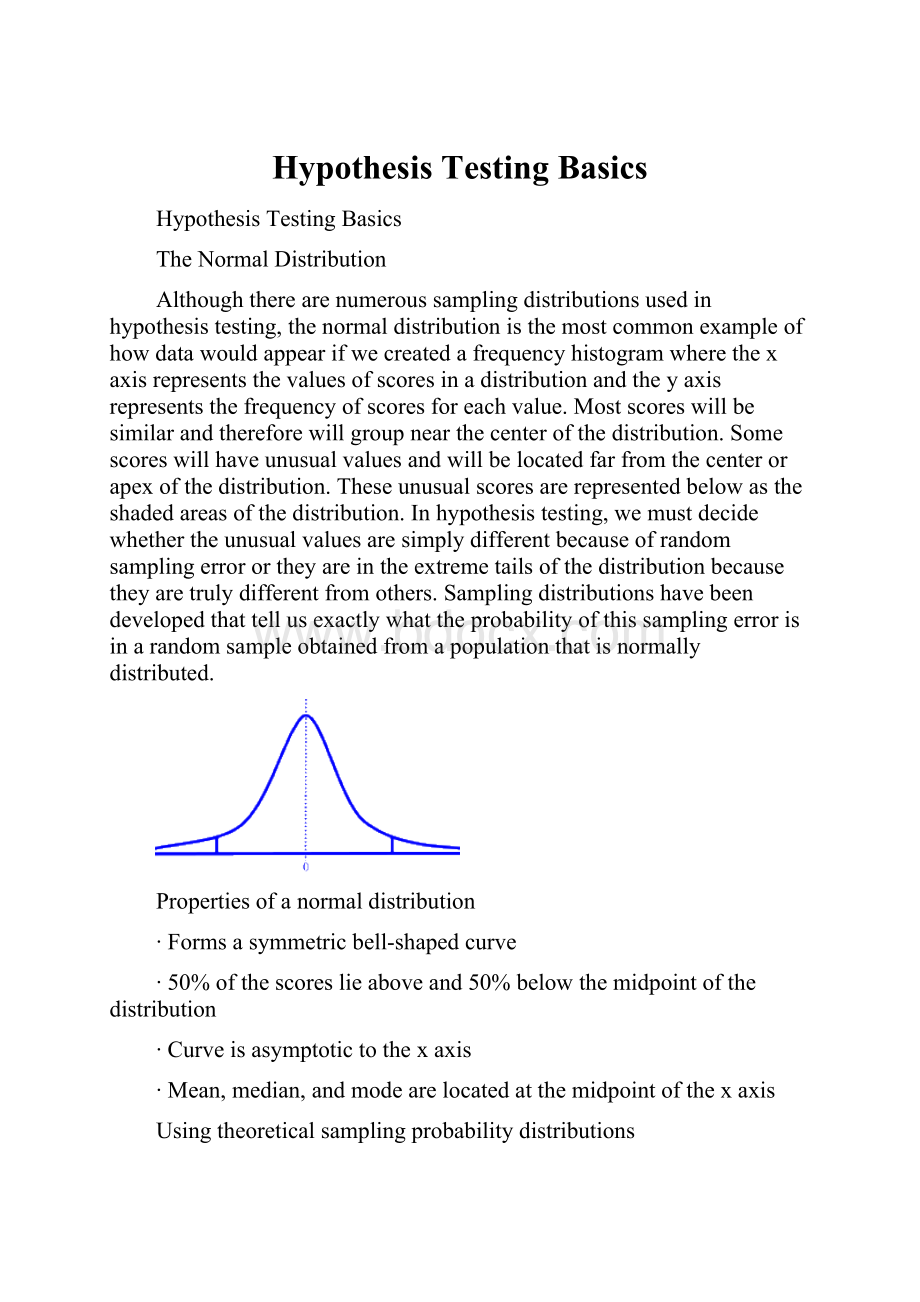
Althoughtherearenumeroussamplingdistributionsusedinhypothesistesting,thenormaldistributionisthemostcommonexampleofhowdatawouldappearifwecreatedafrequencyhistogramwherethexaxisrepresentsthevaluesofscoresinadistributionandtheyaxisrepresentsthefrequencyofscoresforeachvalue.Mostscoreswillbesimilarandthereforewillgroupnearthecenterofthedistribution.Somescoreswillhaveunusualvaluesandwillbelocatedfarfromthecenterorapexofthedistribution.Theseunusualscoresarerepresentedbelowastheshadedareasofthedistribution.Inhypothesistesting,wemustdecidewhethertheunusualvaluesaresimplydifferentbecauseofrandomsamplingerrorortheyareintheextremetailsofthedistributionbecausetheyaretrulydifferentfromothers.Samplingdistributionshavebeendevelopedthattellusexactlywhattheprobabilityofthissamplingerrorisinarandomsampleobtainedfromapopulationthatisnormallydistributed.

Propertiesofanormaldistribution

∙Formsasymmetricbell-shapedcurve

∙50%ofthescoreslieaboveand50%belowthemidpointofthedistribution

∙Curveisasymptotictothexaxis

∙Mean,median,andmodearelocatedatthemidpointofthexaxis

Usingtheoreticalsamplingprobabilitydistributions

Samplingdistributionsallowustoapproximatetheprobabilitythataparticularvaluewouldoccurbychancealone.Ifyoucollectedmeansfromaninfinitenumberofrepeatedrandomsamplesofthesamesamplesizefromthesamepopulationyouwouldfindthatmostmeanswillbeverysimilarinvalue,inotherwords,theywillgrouparoundthetruepopulationmean.Mostmeanswillcollectaboutacentralvalueormidpointofasamplingdistribution.Thefrequencyofmeanswilldecreaseasonetravelsawayfromthecenterofanormalsamplingdistribution.Inanormalprobabilitydistribution,about95%ofthemeansresultingfromaninfinitenumberofrepeatedrandomsampleswillfallbetween1.96standarderrorsaboveandbelowthemidpointofthedistributionwhichrepresentsthetruepopulationmeanandonly5%willfallbeyond（2.5%ineachtailofthedistribution）.

Thefollowingarecommonlyusedpointsonadistributionfordecidingstatisticalsignificance:

90%ofscores+/-1.65standarderrors

95%ofscores+/-1.96standarderrors

99%ofscores+/-2.58standarderrors

Standarderror:

Mathematicaladjustmenttothestandarddeviationtoaccountfortheeffectsamplesizehasontheunderlyingprobabilitydistribution.Itrepresentsthestandarddeviationofthesamplingdistribution

Alphaandtheroleofthedistributiontails

Thepercentageofscoresbeyondaparticularpointalongthexaxisofasamplingdistributionrepresentthepercentofthetimeduringaninfinitenumberofrepeatedsamplesonewouldexpecttohaveascoreatorbeyondthatvalueonthexaxis.Thisvalueonthexaxisisknownasthecriticalvaluewhenusedinhypothesistesting.Themidpointrepresentstheactualpopulationvalue.Mostscoreswillfallneartheactualpopulationvaluebutwillexhibitsomevariationduetosamplingerror.Ifascorefromarandomsamplefalls1.96standarderrorsorfartheraboveorbelowthemeanofthesamplingdistribution,weknowfromtheprobabilitydistributionthatthereisonlya5%chanceofrandomlyselectingasetofscoresthatwouldproduceasamplemeanthatfarfromthetruepopulationmean.Whenconductingsignificancetesting,ifwehaveateststatisticthatis1.96standarderrorsaboveorbelowthemeanofthesamplingdistribution,weassumewehaveastatisticallysignificantdifferencebetweenoursamplemeanandtheexpectedmeanforthepopulation.Sinceweknowavaluethatfarfromthepopulationmeanwillonlyoccurrandomly5%ofthetime,weassumethedifferenceistheresultofatruedifferencebetweenthesampleandthepopulationmean,andisnottheresultofrandomsamplingerror.The5%isalsoknownasalphaandistheprobabilityofbeingwrongwhenweconcludestatisticalsignificance.

1-tailedvs.2-tailedstatisticaltests

A2-tailedtestisusedwhenyoucannotdetermineaprioriwhetheradifferencebetweenpopulationparameterswillbepositiveornegative.A1-tailedtestisusedwhenyoucanreasonablyexpectadifferencewillbepositiveornegative.Ifyouretainthesamecriticalvaluefora1-tailedtestthatwouldbeusedifa2-tailedtestwasemployed,thealphaishalved（i.e.,.05alphawouldbecome.025alpha）.

HypothesisTesting

Thechainofreasoningandsystematicstepsusedinhypothesistestingthatareoutlinedinthissectionarethebackboneofeverystatisticaltestregardlessofwhetheronewritesouteachstepinaclassroomsettingorusesstatisticalsoftwaretoconductstatisticaltestsonvariablesstoredinadatabase.

Chainofreasoningforinferentialstatistics

1.Sample（s）mustberandomlyselected

2.Sampleestimateiscomparedtounderlyingdistributionofthesamesizesamplingdistribution

3.Determinetheprobabilitythatasampleestimatereflectsthepopulationparameter

Thefourpossibleoutcomesinhypothesistesting

ActualPopulationComparison

NullHyp.True

NullHyp.False

DECISION

（thereisnodifference）

（thereisadifference）

RejectedNullHyp

TypeIerror

（alpha）

CorrectDecision

DidnotRejectNull

CorrectDecision

TypeIIError

（Alpha=probabilityofmakingaTypeIerror）

Regardlessofwhetherstatisticaltestsareconductedbyhandorthroughstatisticalsoftware,thereisanimplicitunderstandingthatsystematicstepsarebeingfollowedtodeterminestatisticalsignificance.Thesegeneralstepsaredescribedonthefollowingpageandinclude1）assumptions,2）statedhypothesis,3）rejectioncriteria,4）computationofstatistics,and5）decisionregardingthenullhypothesis.Theunderlyinglogicisbasedonrejectingastatementofnodifferenceornoassociation,calledthenullhypothesis.Thenullhypothesisisonlyrejectedwhenwehaveevidencebeyondareasonabledoubtthatatruedifferenceorassociationexistsinthepopulation（s）fromwhichwedrewourrandomsample（s）.

Reasonabledoubtisbasedonprobabilitysamplingdistributionsandcanvaryattheresearcher'sdiscretion.Alpha.05isacommonbenchmarkforreasonabledoubt.Atalpha.05weknowfromthesamplingdistributionthatateststatisticwillonlyoccurbyrandomchancefivetimesoutof100（5%probability）.Sinceateststatisticthatresultsinanalphaof.05couldonlyoccurbyrandomchance5%ofthetime,weassumethattheteststatisticresultedbecausetherearetruedifferencesbetweenthepopulationparameters,notbecausewedrewanextremelybiasedrandomsample.

Whenlearningstatisticswegenerallyconductstatisticaltestsbyhand.Inthesesituations,weestablishbeforethetestisconductedwhatteststatisticisneeded（calledthecriticalvalue）toclaimstatisticalsignificance.So,ifweknowforagivensamplingdistributionthatateststatisticofplusorminus1.96wouldonlyoccur5%ofthetimerandomly,anyteststatisticthatis1.96orgreaterinabsolutevaluewouldbestatisticallysignificant.Inananalysiswhereateststatisticwasexactly1.96,youwouldhavea5%chanceofbeingwrongifyouclaimedstatisticalsignificance.Iftheteststatisticwas3.00,statisticalsignificancecouldalsobeclaimedbuttheprobabilityofbeingwrongwouldbemuchless（about.002ifusinga2-tailedtestortwo-tenthsofonepercent;0.2%）.Both.05and.002areknownasalpha;theprobabilityofaTypeIerror.

Whenconductingstatisticaltestswithcomputersoftware,theexactprobabilityofaTypeIerroriscalculated.Itispresentedinseveralformatsbutismostcommonlyreportedas"p<"or"Sig."or"Signif."or"Significance."Using"p<"asanexample,ifaprioriyouestablishedathresholdforstatisticalsignificanceatalpha.05,anyteststatisticwithsignificanceatorlessthan.05wouldbeconsideredstatisticallysignificantandyouwouldberequiredtorejectthenullhypothesisofnodifference.Thefollowingtablelinkspvalueswithabenchmarkalphaof.05:

P<

Alpha

ProbabilityofTypeIError

FinalDecision

.05

.05

5%chancedifferenceisnotsignificant

Statisticallysignificant

.10

.05

10%chancedifferenceisnotsignificant

Notstatisticallysignificant

.01

.05

1%chancedifferenceisnotsignificant

Statisticallysignificant

.96

.05

96%chancedifferenceisnotsignificant

Notstatisticallysignificant

StepstoHypothesisTesting

Hypothesistestingisusedtoestablishwhetherthedifferencesexhibitedbyrandomsamplescanbeinferredtothepopulationsfromwhichthesamplesoriginated.

GeneralAssumptions

∙Populationisnormallydistributed

∙Randomsampling

∙Mutuallyexclusivecomparisonsamples

∙Datacharacteristicsmatchstatisticaltechnique

Forinterval/ratiodatauseÊ

t-tests,Pearsoncorrelation,ANOVA,regression

Fornominal/ordinaldatauseÊ

Differenceofproportions,chisquareandrelatedmeasuresofassociation

StatetheHypothesis

NullHypothesis（Ho）:

Thereisnodifferencebetween___and___.

AlternativeHypothesis（Ha）:

Thereisadifferencebetween__and__.

Note:

Thealternativehypothesiswillindicatewhethera1-tailedora2-tailedtestisutilizedtorejectthenullhypothesis.

Hafor1-tailtested:

The__of__isgreater（orless）thanthe__of__.

SettheRejectionCriteria

Thisdetermineshowdifferenttheparametersand/orstatisticsmustbebeforethenullhypothesiscanberejected.This"regionofrejection"isbasedonalpha（

）--theerrorassociatedwiththeconfidencele