关于行列式的一般定义和计算方法.docx

资源描述

关于行列式的一般定义和计算方法.docx

《关于行列式的一般定义和计算方法.docx》由会员分享，可在线阅读，更多相关《关于行列式的一般定义和计算方法.docx（28页珍藏版）》请在冰豆网上搜索。

关于行列式的一般定义和计算方法.docx

关于行列式的一般定义和计算方法

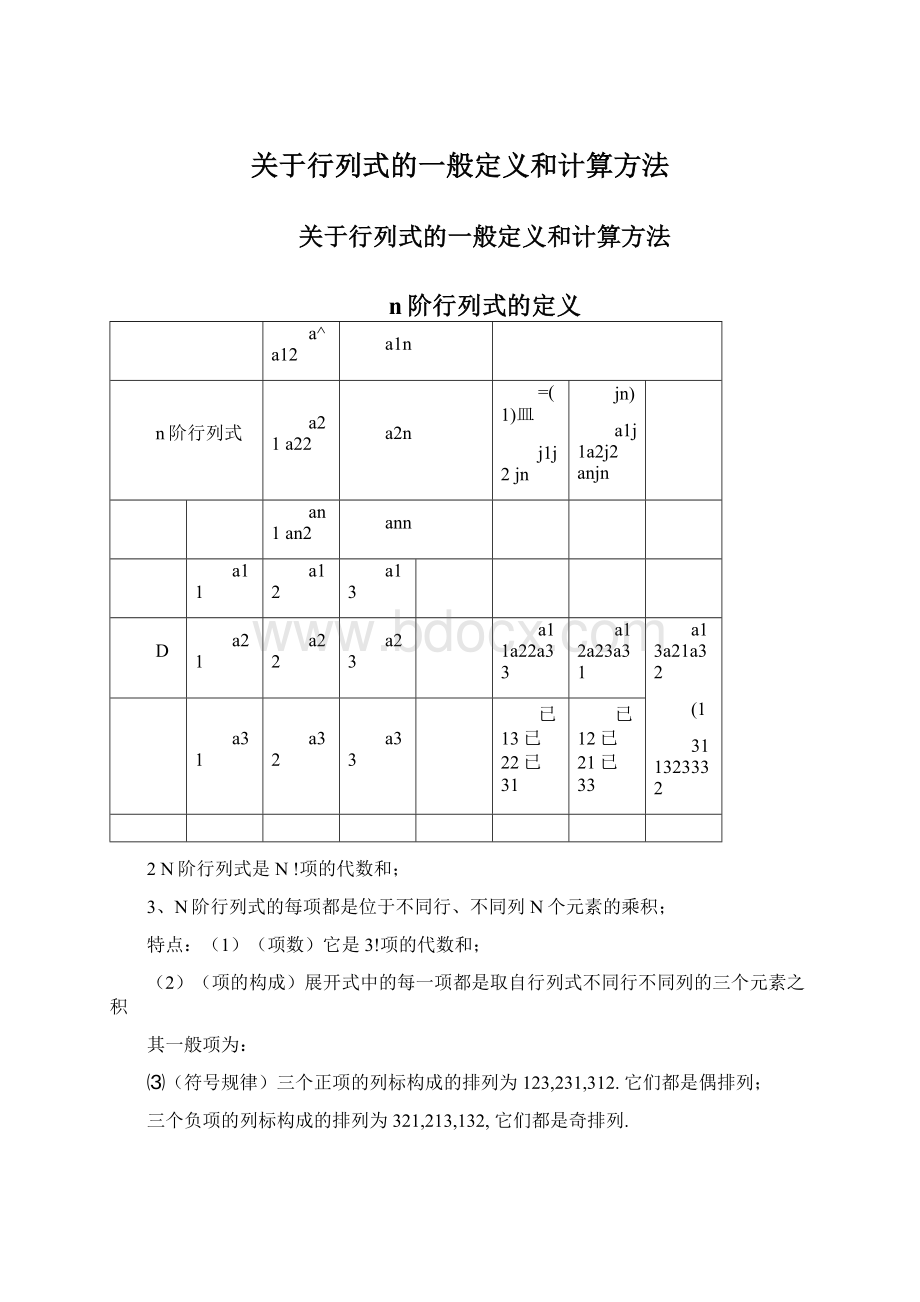
n阶行列式的定义

a^a12

a1n

n阶行列式

a21a22

a2n

（1）皿

j1j2jn

jn）

a1j1a2j2anjn

an1an2

ann

a11

a12

a13

a21

a22

a23

a11a22a33

a12a23a31

a13a21a32

（1

311323332

a31

a32

a33

已13已22已31

已12已21已33

2N阶行列式是N!

项的代数和；

3、N阶行列式的每项都是位于不同行、不同列N个元素的乘积；

特点：

（1）（项数）它是3!

项的代数和；

（2）（项的构成）展开式中的每一项都是取自行列式不同行不同列的三个元素之积

其一般项为：

⑶（符号规律）三个正项的列标构成的排列为123,231,312.它们都是偶排列；

三个负项的列标构成的排列为321,213,132,它们都是奇排列.

§行列式的性质

，性质1:

行列式和它的转置行列式的值相同。

ai1ai2

ain

ai1a21

an1

即

a21a22

a2n

ai2a22

an2

anian2

ann

aina2n

ann

行列式对行满足的性质对列也同样满足。

性质2互换行列式的两行（列），行列式的值变号.

匚ab

如:

D==ad-bccd

=bc-ad=-D

以ri表第i行，Cj表第j列。

交换i,j两行记为ri「,交换i,j两列记作

性质3：

如果一个行列式的两行（或两列）完全相同，那么这个行列式的值

等于零。

"性质4：

把一个行列式的某一行（或某一列）的所有元素同乘以某一个常数k

的结果等于用这个常数k乘这个行列式。

（第i行乘以k，记作rik）

推论1：

一个行列式的某一行（或某一列）的所有元素的公因式可以提到行

列式符号的前面。

推论2：

如果一个行列式的某一行（或某一列）的所有元素都为零，那么行

列式值等于零。

推论3：

如果一个行列式的某二行（或某二列）的对应元素成比例，那么行列

式值等于零。

a11

ai2

ain

aii

ai2

ain

kaii

kai2

kain

ai1

ai2

ain

an1

an2

ann

ani

an2

ann

，性质5：

如果行列式D的某一行（或某一列）的所有元素都可以表成两项的和，那么行列式D等于两个行列式Di和D2的和

a11a12

a1j

a1n

a11a12

a1j

a1n

a12

a1n

a21a22

a2j

a2n

a21a22

a2j

a2n

a21

a22

a2n

an1an2

anj

ann

an1an2

anj

ann

an1

an2

ann

性质6:

把行列式的某一行（或某一列）

的元素乘同一个数后,

加到另一行（或

另一列）的对应元素上，行列式值不变。

推论如果行列式的某一行（列）的每个元素都是m个数之和（m>2），则此行列式等于m个行列式之和。

定义：

行列式aij如果满足：

aijaji（i,j1,,n）；

则称此行列式为对称行列式。

一个n阶行列式，如果它的元素满足：

aijajii,j1,2n；试证：

当n为奇数时，此行列式为零。

每一行（或列）提出一个（-1），再转置得D=（-1）nD

性质7行列式的某一行（列）的各元素与另一行（列）的对应元素的代数余子式的乘积之和等于零。

按仃：

ai1Aj1ai2Aj2ainAjn0ij

按列：

a1iA1ja2iA2janiAnj0ij

将性质7与Laplace定理合并为下列结论：

nDi

aikAjk

k10i

（1）

亍nDi

和aS门-

（2）

k10i

行列式的计算

1•利用行列式定义直接计算

例1计算行列式

解Dn中不为零的项用一般形式表示为

ain1a2n2Laniiannn!

・

该项列标排列的逆序数t（n-1n—2…1n）等于（n1）（n_◎，故

（n1）（n2）

（1）2nL

2•利用行列式的性质计算

例2一个n阶行列式Dnaij的元素满足

ajaji,i,j1,2丄，n,

则称Dn为反对称行列式，证明：

奇数阶反对称行列式为零.

证明：

由aj

aji知aii

a，即

aii

0,i

1,2,L

故行列式Dn

可表示为

a12

a1n

a12

a23

a2n

a13

a23

a3n

a1n

a2n

a3n

由行列式的性质A

a12

a13

a1n

a12

a23

a2n

a13

a23

a3n

a1n

a2n

a12

a13

a1n

a12

a23

a2n

（1）n

a13

a23

a3n

a1n

a2n

a3n

（1）n

当n为奇数时，得Dn=—Dn，因而得Dn=0.

3.化为三角形行列式

若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。

因此化三角形是行列式计算中的一个重要方法。

（n

1）b

1）b]

abL

1）b]（a

abL

b）n1

bbL

例3计算n阶行列式

解：

这个行列式的特点是每行（列）元素的和均相等，根据行列式的性质,把第2,3,…，n列都加到第1列上，行列式不变，得

4•降阶法

降阶法是按某一行（或一列）展开行列式，这样可以降低一阶，更一般地是用拉普拉斯定理，这样可以降低多阶，为了使运算更加简便，往往是先利用列式的性质化简，使行列式中有较多的零出现，然后再展开。

例4计算n阶行列式

解将Dn按第1行展开

Dna

（

1）n1

（1）

n1z

（

1）

5•逆推公式法

逆推公式法：

对n阶行列式Dn找出Dn与Dn—1或Dn与Dn-1,Dn—2之间的一种关系一一称为逆推公式（其中Dn,Dn—1,Dn—2等结构相同），再由递推公式求出Dn的方法称为递推公式法。

例5证明

an1

an2

a1x

an1X

an,（n2）

证明：

将Dn按第1列展开得

Dnx

an1

an2

an3

a1x

（1）an

anXDn

由此得递推公式：

DnanxDn1，利用此递推公式可得

XDn1anX（an1xDn2）

ananiXXDn2

aniXL

n1n

a-|Xx

6•利用范德蒙行列式

例6计算行列式

X21

X2X2

n1n2

X2X2

Xn1

XnXn

n1n2

XiXn

解把第1行的一1倍加到第2行，把新的第2行的一1倍加到第3行，以

此类推直到把新的第

n—

1行的-1倍加到第n行，便得范德蒙行列式

（XiXj）

nij1

7•加边法（升阶法）

加边法（又称升阶法）是在原行列式中增加一行一列，且保持原行列式不变的方法。

例7计算n阶行列式

xa1

xa2

xan

解：

用数学归纳法•当n=2时

D2x（xa1）a2

a2xa1

xa〔xa2

假设n=k时，有

ikk1k2.

解:

第i行减第1行

i2,L,n1

1a1Lan

MDn

0（箭形行列式）

naj

8•数学归纳法

例8计算n阶行列式

DnLL

anan1

1LLL0Lan2L

x1a2a-ix

Dkxa〔xa2XLak1Xak

则当n=k+1时，把Dk+i按第一列展开，得

Dk1

由此，对任意的正整数n,有

Dnxnaixn1

xDk

ak1

x（xk

ak低

ak）

ak1

Lak

a〔x

akX

ak1

2n2X

an1X

9•拆开法

把某一行（或列）的元素写成两数和的形式,

再利用行列式的性质将原行列

式写成两行列式之和，使问题简化以利计算。

1a2

Lan

计算行列式

ann

解：

a22

刁22

ann

例9

1Dn1

912L

上面介绍了计算n阶行列式的常见方法,

计算行列式时,

我们应当针对具体

问题，把握行列式的特点，灵活选用方法。

学习中多练习，多总结，才能更好地掌握行列式的计算。

axby

（1）aybz

azbx

证明

bzazbxaxbyay

by（a3b3）y

xayyazzax

bzazbxaxbyay

bzbxby

bxbybz

xaybzz

yzazbx

yazbxx

zxaxby

zaxbyy

xyaybz

C代表列••R代表行）

关于行列式的消项（其中

（a

X—

r2a1

2）

明

2）bb2

2a2a1

Qcs

2bb21

X—

a）

2aa2b22b

xyz

yzx

zxy

xyz

yzx

zxy

（a3

b3）y

—24

4ddd

1C2CC41bb2b4

（ab）（ac）（ad）（bc）（bd）（cd）（abcd）;

证明

24dd

1c$

1bb2b4

（C2,C3,C4减数字去第

1111

0bacada

0b（ba）c（ca）d（da）

0b2（b2a2）c2（c2a2）d2（d2a2）

列的）

（ba）（ca）（d

111

a）bcd

b2（ba）c2（ca）d2（d

a）

（ba）（ca）（d

a）0cb

0c（cb）（cba）d（d

1dbb）（dba）

（ba）（ca）（da）（cb）（db）c（cba）d（dka）

xoo^

T—

oan

乂

naX

X2a

T—

证明用数学归纳法证明

当n2时D2jx!

x2qxa2命题成立

假设对于（n1）阶行列式命题成立即

Dn1xn1a1xn2an2Xan1

则Dn按第一列展开有

T—

00X

xDn1anxna1Xn

因此对于n阶行列式命题成立6设n阶行列式Ddet（aij）,

90、或依副对角线翻转依次得

把D上下翻转、或逆时针旋转

1Xan

an1

ann

ain

ann

ain

ai1

a1n

ai1

an1

cl|1

n（n1）

1）丁DD3

证明D1

证明

（

因为Ddet（aj）

所以

an1

ann

（1）n1

ai1

an1

ainann

ai1

ain

a21

a2n

（1）n1（

1）n2

aii

a21

an1

ain

a2n

ann

（1）12

同理可证

（n2）（n

1）D

n（n1）

1）丁D

n（n1）

（1）2

aii

ann

n（n1）

（1）丁DT（

n（n1）

1）丁D

n（n1）

（1）62

n（n1）

1）丁（

7计算下列各行列式

（

（Dk为k阶行列式）

n（n1）

1）丁D

（1）n（n1）DD

（1）Dn

其中对角线上元素都是a未写出的元素都

X—

（按第n行展开）

（1）2na

a（n1）（n1）

（n1）（n1）

T—

（a

⑵Dn

解将第一行乘

（1）分别加到其余各行得

xaaa

axxa00

ax0xa0

ax000xa

再将各列都加到第一列上得

⑶Dn1

noo

aao

XaaoXa

aoo

an（a1）n

an1（a1）n1

aa1

[x（n1）a]（xa）n1

000xa

（an）n

（an）n1

解根据第6题结果有

n（n1）

（1）2

an1

（a

1）n1

1）n

（an）n1

（an）n

此行列式为范德蒙德行列式

n（n1）

Dn1（厂[（ai1）（aj1）]

n1ij1

n（n1）

（1）F[（ij）]

例3

n1ij1

0aba

2ab2ab2ab2ab

a0ab

r1r2r3r4

a0ab

ba0a

aba0

n（nDn（n1）1

（1）F

（1）—2—（ij）

n1ij1

12ab

「2A

2ab

Bar1

r3br1

0ba

2ab

bab

2abab

abab

baa

0ba

bab2ab

2ab

ba2ba2b44a2b2

2sin

cos

cos2

练习3:

证明：

证明:

左边

sin

cos

cos2

2-2

-2sin

2cos

cos2

cos

2cos

12cos2

cos

12cos21

COS

cos

从最后一行开始，每行减去上一行，得到:

123...

111...

n-1n

11-n

11-n1

...11

然后做列变换，从各列中减去第一列，得到:

112...

n-2n-1

100...

0-n

1-n0..

.00

再把各列乘以（1/n），加回到第一列，得到：

（n+1）/2

12...n-2n-1

000...

0-n

0-n0…00

最后沿第一列展开得到结果是（1/2）*（n+1）*n^{n-1}*（-1）化（n-1）（n-2）/2}

展开阅读全文