奥林匹克数学竞赛试题.docx

奥林匹克数学竞赛试题.docx

《奥林匹克数学竞赛试题.docx》由会员分享，可在线阅读，更多相关《奥林匹克数学竞赛试题.docx（8页珍藏版）》请在冰豆网上搜索。

奥林匹克数学竞赛试题

奥林匹克数学竞赛试题（几何部分）MathematicsOlympictest

（geometricpart）

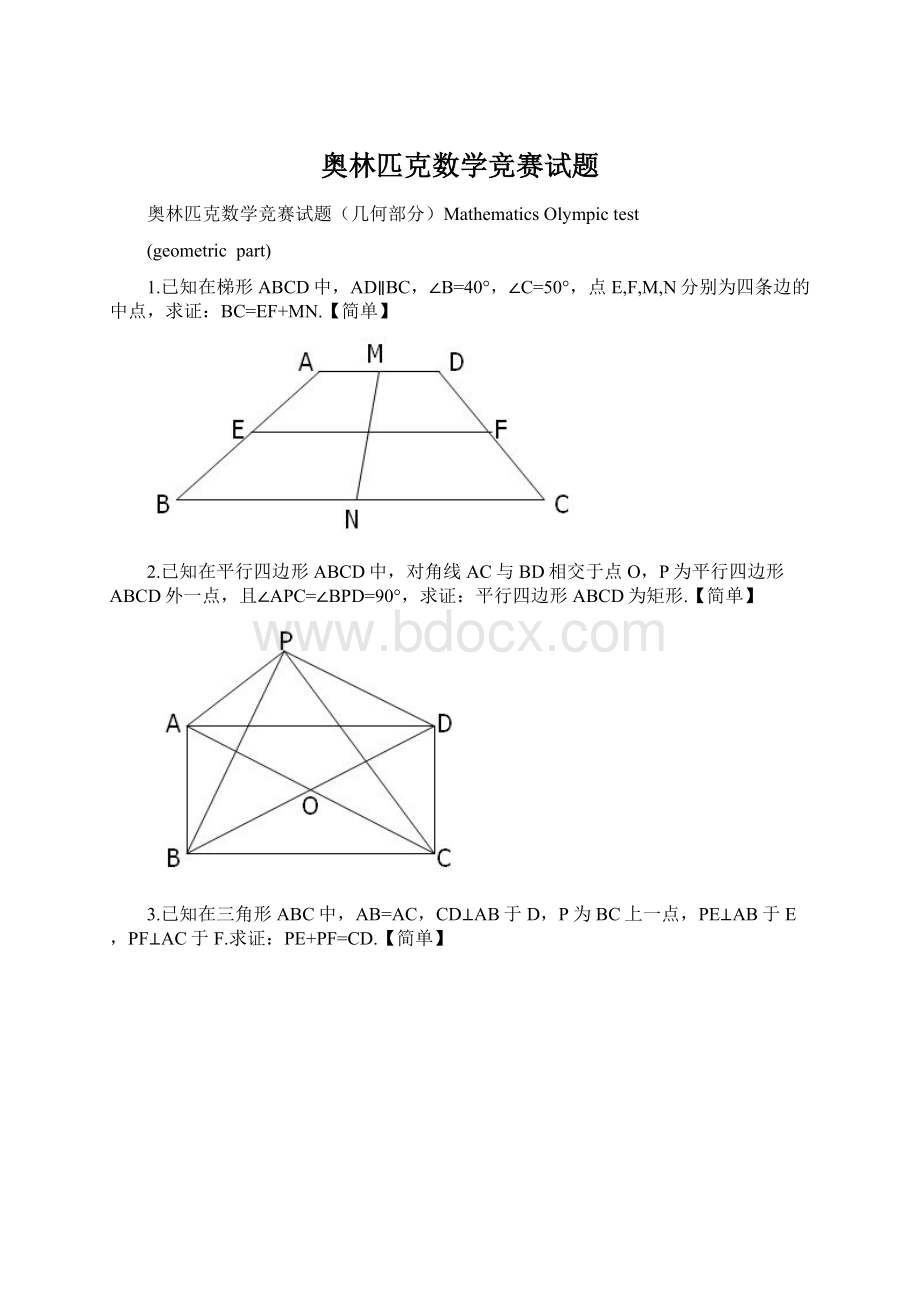
1.已知在梯形ABCD中，AD∥BC，∠B=40°，∠C=50°，点E,F,M,N分别为四条边的中点，求证：

BC=EF+MN.【简单】

2.已知在平行四边形ABCD中，对角线AC与BD相交于点O，P为平行四边形ABCD外一点，且∠APC=∠BPD=90°，求证：

平行四边形ABCD为矩形.【简单】

3.已知在三角形ABC中，AB=AC，CD⊥AB于D，P为BC上一点，PE⊥AB于E，PF⊥AC于F.求证：

PE+PF=CD.【简单】

4.已知在等腰三角形ABC中，AB=AC，CD⊥AB，AH⊥FH，EF⊥AB，求证：

EF=CD+FH.【简单】

5.已知三角形ABC和三角形BDE都是等腰直角三角形，连结AD，延长CE交AD与F,求证：

CF⊥AD.【简单】

6.已知三角形ABC和三角形BDE都是正三角形，连结AD交BE于F，连结CE交AB于G，连结FG，求证：

FG∥CD.【简单】

7.已知三角形ABC为正三角形，内取一点P，向三边作垂线，交AB于D，BC于E,AC于F，求证：

PD+PE+PF=三角形的高.【简单】

8.已知三角形ABC为正三角形，AD为高，取三角形外一点P，向三边（或边的延长线）作垂线，交AB的延长线AE于M，交AC的延长线AF于N，交BC于Q，求证：

PM+PN-PQ=AD.【中等】

9.已知在矩形ABCD中，对角线AC,BD相交于O，DE平分∠ADC交AC于F，若∠BDE=15°，求∠COE的度数.【中等】

10.已知三角形ABC是直角三角形，∠BAC=90°，AD⊥BC，AE平分∠CAD，BF平分∠ABC，交AD于G，交AE于H，连结EG,求证：

EG∥AC.【中等】

11.已知三角形ABC和三角形BDE都是正三角形，连结AE,CD,取AE的中点N，取CD的中点M，连结BM,BN,MN.求证：

三角形BMN是等边三角形.【中等】

12.已知在正方形ABCD中，作对角线AC的平行线EG，作BC=CH，连结BE，延长HG交BE于F，连结CF，求证：

BC=CF.【中等】

13.已知在直角梯形ABCD中，AD∥BC，AD=3，BC=5，将腰CD绕点D逆时针旋转90°至DE，连结AE，求三角形ADE的面积.【中等】

14.已知在任意四边形ABCD中，AB=CD，P,Q,R分别为AD,BC,BD的中点，∠ABD=25°，∠BDC=65°，求∠PQR的度数.【中等】

15.已知在梯形ABCD中，AD∥BC，E为AB的中点，求证：

S三角形CDE=S三角形ADE+S三角形BCE.【较难】

16.已知矩形ABCD，在CD的延长线上取一点E，在BC的延长线上取一点F，使得∠DAE=∠DAF,AF和CD交于G,求证：

S矩形ABCD=S三角形AEF.【较难】

17.已知在等腰直角三角形ABC中，∠BAC=90°，AD=AE，AF⊥BE交BC于F，过F作FG⊥CD交BE的延长线于G，求证：

BG=AF+FG.

【很难】【提示：

过C点作AC的垂线，延长AF，交垂线于H.】

18.已知在正九边形ABCDEFGHI中，连结AE，AE=1,求AH+AI的长.【很难】【提示：

延长AH使HK=HG，连结KG.】

19.已知正方形ABCD内有一点P，且PB：

PC：

PD=3：

2：

1，求证：

∠CPD=135°.【超难】【提示：

过C作PC的垂线CP’，使CP=CP’.】

20.已知在任意四边形ABCD中，点E,F分别将AD,BC分成m：

n两部分，AF和BE交于P，CE和DF交于Q，求证：

S四边形EPFQ=S三角形CDQ+S三角形ABP.【超难】