Possion方程的差分法求解.docx
《Possion方程的差分法求解.docx》由会员分享,可在线阅读,更多相关《Possion方程的差分法求解.docx(13页珍藏版)》请在冰豆网上搜索。
Possion方程的差分法求解
Possion方程的差分方法
课程名称:
微分方程数值解
学生姓名:
张弘
、问题描述
Possion方程的差分方法
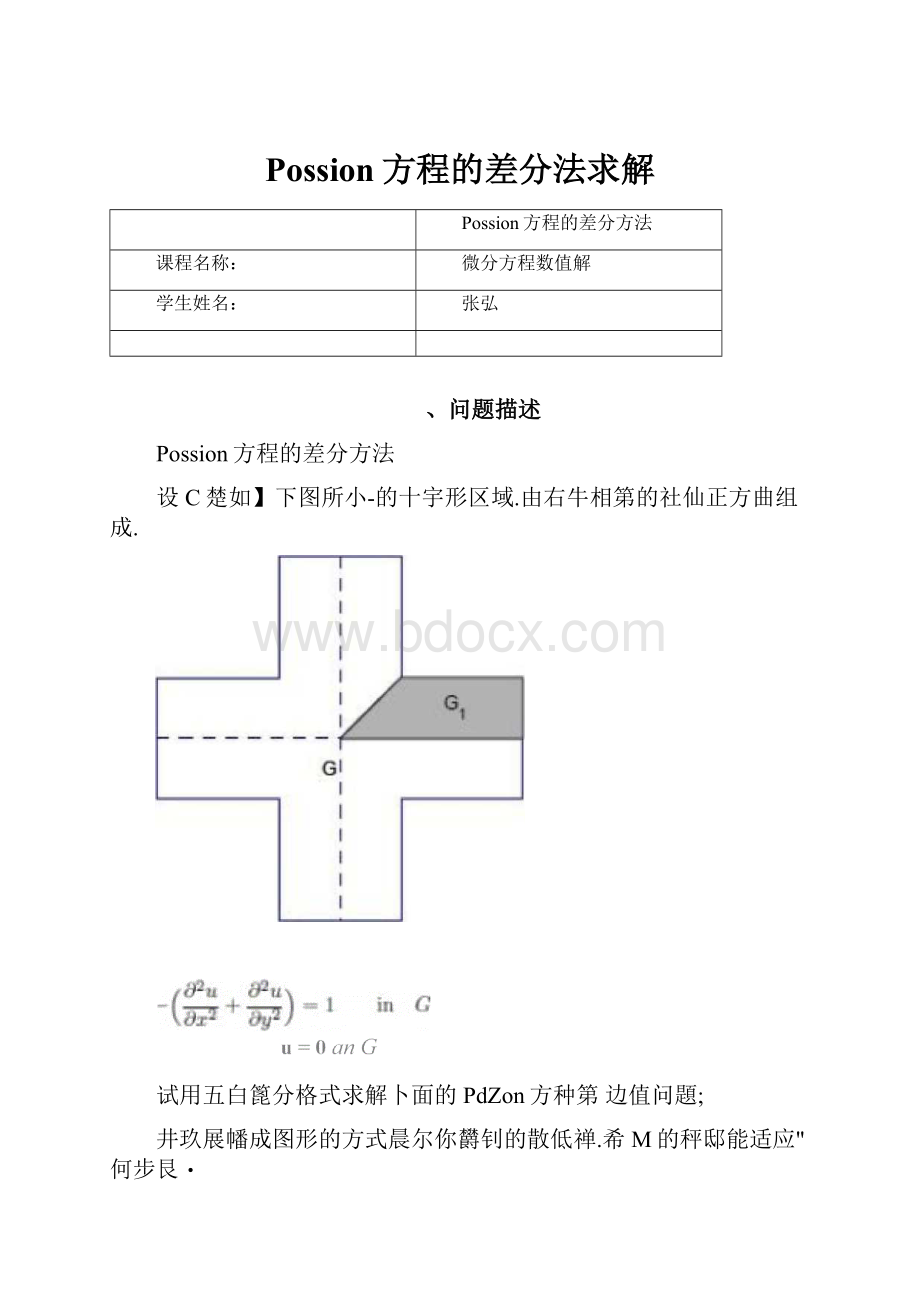
设C楚如】下图所小-的十宇形区域.由右牛相第的社仙正方曲组成.
试用五白篦分格式求解卜面的PdZon方种第边值问題;
井玖展幡成图形的方式晨尔你欝钊的散低禅.希M的秤邸能适应"何步艮・
提示:
由邑域和犠分方程的对称性’貝城從如圏阴慚所於的八井2陲域岱上求解即吋佛能证期進ijft吗》I。
将连续问题离散化的步骤是:
1、对求解区域做网格剖分用有限个网格节点代替连续区域。
2、微分算子离散化。
3、把微分方程的定解问题化为线性代数方程组的求解问题。
差分法和有限元方法的主要区别是离散化的第二步,差分法从定解问题的微分或积分形式出发,用数值微商或数值积分公式到处相应的线性代数方程组,有限元法从定解问题的变分形式出发,用Ritz-Galerkin法导出相应的线性代数方程组。
差分法的基本问题有:
(1)对求解区域做网格剖分
一维情形为把区间分为等距或不等距的区间,二维情形是把区域分割成均匀或不均匀的矩形,其边与坐标轴平行,也可分割成小三角形或凸四边形。
(2)构造逼近微分方程定解问题的差分格式
有两种构造差分格式的方法:
直接差分化法和有限体积法。
(3)差分解的存在唯一性,收敛性和稳定性研究
(4)差分方程的解法:
逐次超松弛法,交替方向法,共轭梯度法。
II
(1)由题目可知,本题需要考虑矩形网的五点差分格式。
题目给出的为第一边值条件,将十字形图形的中心放于坐标原点处,如下图所示:
由图形可知,所给区域可以看出是由8个梯形G1通过旋转、翻转拼接而成。
因此为了
方便计算、减少计算量,只针对G1进行网格剖分,用5点差分格式进行求解。
但是由于
G1是直角梯形,进行网格剖分时会出现x轴方向网格点个数不同的现象,不利于有差分形
成的系数矩阵的生成,所以将三角形S1和梯形G1合在一起形成一个矩形,其区域为
[0,3/2][01/2]。
如果采用等距差分,并且有hx=hy=h,设步长为h,
x=0:
h:
3/2;y=0:
h:
1/2;
nx=length(x)-1;%为所求区域中x轴上内点的个数ny=length(y)-1;%为所求区域中y轴上内点的个数
对于原来的梯形G1来说,有网格内点nx*ny-(ny^2-my)/2
对于矩形区域S1+G1而言,网格内点数为nx*ny,所以在后面的程序中要比在梯形G1中多
计算了(nyA2-my)/2个点的函数值,但对程序效率的影响并不是很大,可以接受。
以下具体说明只需在G1上求解poisson方程的原因
所求方程为:
设直线I是经过原点0的任意一条直线,其方程为:
y=kx
设p(x,y)是区域内任一点,则其关于I对称的点为p'(s,t)
S=((k-1)A2+|2y)/(kA2+1)t=(2kx+(kA2-1)y)/(kA2+1)
同理可得:
ud:
;1)2
2
/2k、2“2k(k-1)
Uyy—Uss
(2)2ust22
yy1k2(1k2)2
将u(s,t)代替u(x,y)得:
Uxx+Uyy=Uss+Utt=1
其依然满足上述方程。
令0=arctan(k)点p的横坐标x=rcos(a)y=rsin(a)
则p关于直线I的对称点为p'(rcos(2-a),rsin(2-a0)
由上述证明可知u(p)=u(p')。
条经过原点直线I
由0和p点的任意性知,对于函数u图像上的任意一点p,其关于任意一的对称点p'都在u的图像上,即u(a+S)=u(即)u关于原点是旋转对称的。
当I为x轴时,有u(x,y)=u(x,-y)l为y轴时,u(x,y)=u(-x,y)
坐标轴旋转不改变方程的形式,所以函数在直角坐标系中U关于原点是旋转对称的,又所
求十字形区域关于x,y轴是轴对称和关于原点中心对称的,因此可通过直求解区域G1,
就可以知道函数在整个十字形区域的图像。
(2)对S1+G1形成的矩形进行正方形网格剖分,则求解Poisson方程的差分格式和化为如
下形式:
对于正则内点其差分如下:
-△u=1/hA2*(-u(i,j+1)-u(i-1,j)+4u(i,j)-u(i+1,j)-u(i,j-1))=fj⑴
对于矩形区域S1+G1,nx=(xb-xa)/h-1ny=(yb-ya)/h-1
按从左到右,从下到上的次序排列网点(ij):
j=1,1向量
Uh=[U11,U21…,unx-1;…;u1nx-1,u2,nx-1,…,Uy-1,nx-1]
利用边界条件可以将
(1)式写成如下形式:
1A
「2AUh=g
h
_B-I1
-IB-I
其中A=为nx*ny阶矩阵,I为nx阶单位矩阵,B为nx阶单
—IB—I
:
.-IB
位矩阵。
-
4-1
-1
4
-1
B=
-1
4
—1
1
-1
4
右端向量g的元素,依赖于边值a和右端项f,显然A是对称正定矩阵,也是稀疏矩阵因此可以采用逐次超松弛法,共轭梯度法和交替方向法莱求解,但为了方便程序设计采用了
matlab的‘运算符来求解u。
针对本题的Poisson方程,对S1+G1形成的矩形网格的五点差分的具体分析。
对S1+G1形成的矩形五点差分的具体分析。
3/2
红色线条围成的区域为G1,L为红色斜边,S1为L左侧的三角形,S2为L右侧的三角形。
由对称性知,S1和S2中关于L相互对称的网格点其上U的函数值是相同的。
按从左到右,从下到上的次序排列网点(ij)。
(1)
对于三角形S1中的网点有u(i,j),ny>i>j》1,有u(i,j)-u(j,i)=O
所以S1中网点的差分就为:
u(i,j)-u(j,i)=O
(2)由于原点o点的特殊性,其邻点中u(1,2)=u(1,-1)=u(-1,1)=u(2,1)
所以其差分为:
u(1,1)-4u(1,2)=hA2*f(i,j)
程序中语句:
A(1:
nx,nx+1:
2*nx)=2*l;和A(1,2)=-2;
保障了上面差分方程的系数。
(3)对于网格上最下面一行上除了原点o的所有正则网格内点,由对称性得u(1,i)的邻点中
u(1,i-1)=u(1,i+1)
所以其差分为:
4u(i,j)-u(i-1,j)-u(i+1,j)-2*u(i,j+1)=hA2*f(i,j)
对于右下角的非正则内点u(1,nx)
其差分为:
4u(i,j)-u(i-1,j)-2*u(i,j+1)=hA2*f(i,j)
程序中的相关语句为:
A(1:
nx,nx+1:
2*nx)=2*l;
A(nx+1:
2*nx,nx+1:
2*nx)=B;
(4)对于G1中的所有正则内点,其差分为:
4u(i,j)-u(i-1,j)-u(i+1,j)-u(i,j-1)-u(i,j+1)=hA2*f(i,j)
程序中相关语句:
A(i*nx+1:
(i+1)*nx,i*nx+1:
(i+1)*nx)=B;
A((i-1)*nx+1:
i*nx,i*nx+1:
(i+1)*nx)=l;
A(i*nx+1:
(i+1)*nx,(i-1)*nx+1:
i*nx)=l;
⑸对于网格最后一列的所有非正则内点u(:
nx),其差分为:
4u(nx,j)-u(nx,j-1)-u(nx,j+1)-u(nx-1,j)=hA2*f(i,j)
(6)在求出了所有的内点后,对于剩下的边界点赋值有:
U(ny+1,ny+1:
nx)=O%最上面一行上的边界点
U(1:
ny+1,nx+1)=0%最右侧一列的边界点
u(ny+1,1:
ny)=u(1:
ny,ny+1);%三角形S1和S2边界上的网点,它们是S1的边界点,但是
整个求解区域的内点。
三、程序设计及分析
functionpoisson5spot(h)
ifnargi*1%默认步长h=0.02
h=0.02;
end
x=0:
h:
3/2;
y=0:
h:
1/2;
nx=length(x)-1;%取区域的内点
ny=length(y)_1;
%===========构造矩阵b==========
B=eye(nx,nx)*4;
fori=1:
nx-1
B(i,i+1)=-1;
end
fori=2:
nx
B(i,i-1)=-1;
end
I=-eye(nx,nx);
%===========构造系数矩阵A========
A=zeros(nx*ny,nx*ny);
A(1:
nx,1:
nx)=B;
%由区域的对称性,正方形网格最下面一行的差分形式
%改为4u(i,j)-u(i-1,j)-u(i+1,j)-2*u(i,j+1)
%因为u(i,j+1)=u(i,j-1)
A(1:
nx,nx+1:
2*nx)=2*l;
A(nx+1:
2*nx,nx+1:
2*nx)=B;
%矩形网格左下角第一个点的差分形式改为:
%4u(i,j)-u(i-1,j)-u(i+1,j)-u(i,j+1)-u(i,j-1)
%=4u(i,j)-2u(i,j+1)-2u(i+1,j)
A(1,2)=-2;
%为了方便,本程序往梯形中增加了一个三角形,以方便编程
A(nx+1:
2*nx,1:
nx)=l;
fori=2:
ny-1
A(i*nx+1:
(i+1)*nx,i*nx+1:
(i+1)*nx)=B;
A((i-1)*nx+1:
i*nx,i*nx+1:
(i+1)*nx)=l;
A(i*nx+1:
(i+1)*nx,(i-1)*nx+1:
i*nx)=l;
end
%==========================
%bi=h*h*f;右端向量
b=h*h*ones(nx*ny,1);
%由于对称性,左侧三角形中有u(i,j)-u(j,i)=Oi>j
%因此令A(i,j)=1A(j,i)=-1
%所以在本程序中多计算了(nyA2-my)/2个点的函数值
%但对程序的影响并不是很大
fori=2:
ny
A((i-1)*nx+1:
(i-1)*nx+i-1,:
)=0;
forj=1:
i-1
A((i-1)*nx+j,(i-1)*nx+j)=1;
A((i-1)*nx+j,(j-1)*nx+i)=-1;
b((i-1)*nx+j)=0;
end
end
x=A\b;%为了方便采用左除求解网格点上的函数值
%x=gmres(A,b,100);
%按顺序将x赋值给u
u=zeros(ny+1,nx+1);
fori=1:
ny
forj=1:
nx
u(i,j)=x((i-1)*nx+j);
end
end
%根据对称性,给网格最上面一行的点赋值
u(ny+1,1:
ny)=u(1:
ny,ny+1);
%=============作Poisson方程在区域上的图形===========
[x,y]=meshgrid(0:
h:
3/2,0:
h:
1/2);
holdon
surf(x,y,u)%11第一象限的第一块区域,下面的以此类推
surf(y,x,u)%12
surf(-y,x,u)%21
surf(-x,y,u);%22
surf(-x,-y,u)%31
surf(-y,-x,u)%32
surf(y,-x,u)%41
surf(x,-y,u);%42
四、实验结果
1.在区域G1上求解后的图形显示
图形表示了在S1+G1区域上的函数图像,而不是单纯的G1上的函数图像。
2通过拼接后图形显示如下:
Fi*eEdcInsen:
TookDtskiapa.V«idonH«lp
由上图可知,除了边界点外网格点上的函数值都有u(i,j)>0.
LhUj>0,对任意(xi,yj)€Gh,W不可能在内点取得负的极小,与极值定理相符合。
3、翻转后图形如下:
4网格间距h=0.01时得到的图形:
五、实验分析
本次实验将求解区域先利用对称性将其缩小为原区域的1/8,又为了方便系数矩阵的选取给G1添加了三角形S1,减少了运算量。
在实验中通过更改h,发现当h=0.01时,使用matlab的’符号来求解,会发生内存溢出的现象,因此此时系数矩阵A为500*1500=750000,但是如果采用稳定双共轭梯度法
bicgstab和预条件的再开始gmres算法则可以继续求解。
6、参考文献
[1]李荣华,刘播•微分方程数值方法.
[2]胡建伟,汤怀民,微分方程的数值方法.