小升初总复习提纲.docx
《小升初总复习提纲.docx》由会员分享,可在线阅读,更多相关《小升初总复习提纲.docx(23页珍藏版)》请在冰豆网上搜索。
小升初总复习提纲
小升初总复习提纲
第一章数与代数
第一节数的认识
第1课时:
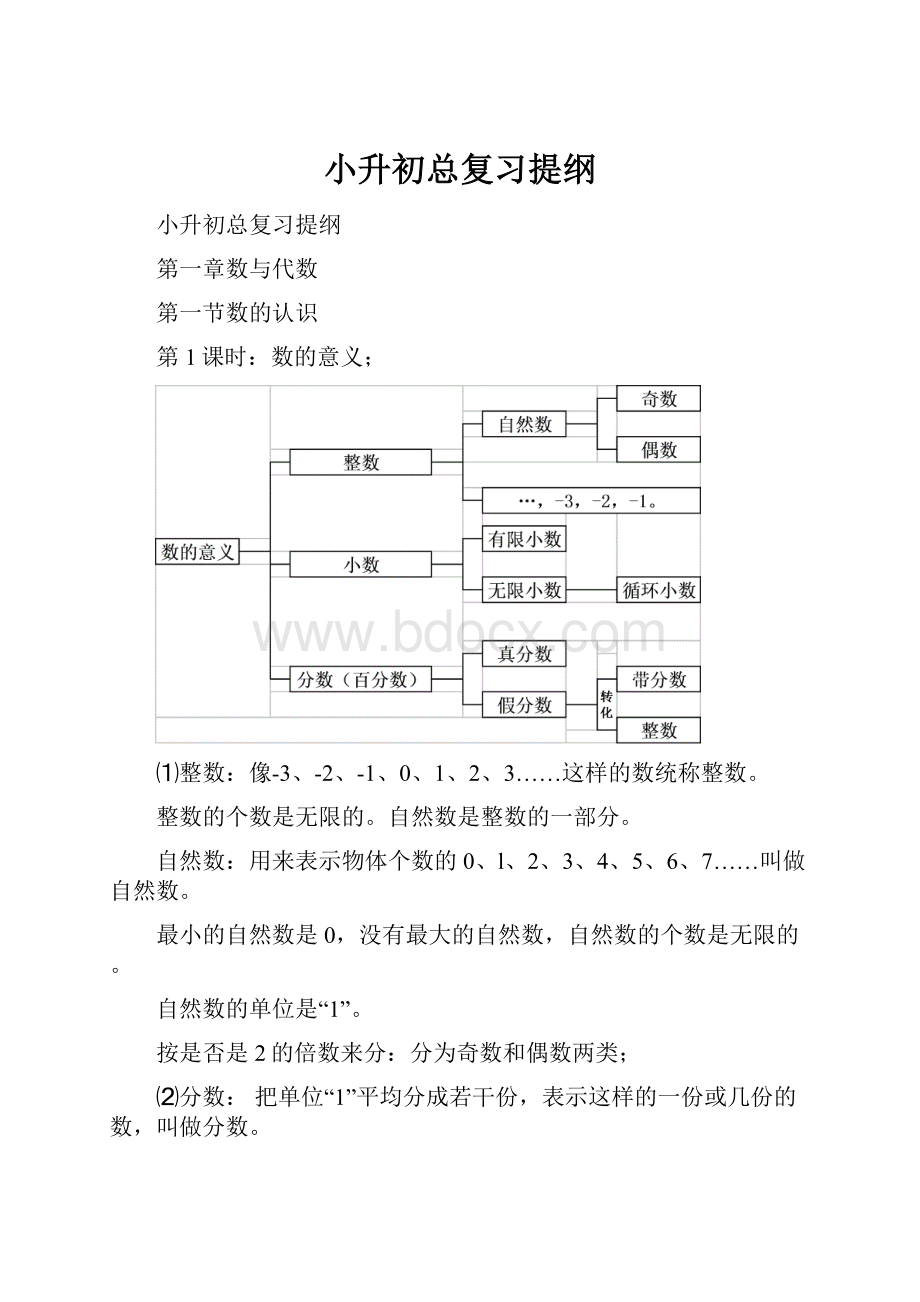
数的意义;
⑴整数:
像-3、-2、-1、0、1、2、3……这样的数统称整数。
整数的个数是无限的。
自然数是整数的一部分。
自然数:
用来表示物体个数的0、l、2、3、4、5、6、7……叫做自然数。
最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
自然数的单位是“1”。
按是否是2的倍数来分:
分为奇数和偶数两类;
⑵分数:
把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
表示其中一份的数叫做分数单位。
例如:
的分数单位是
,它有7个这样的分数单位。
真分数:
分子比分母小的分数叫真分数。
真分数小于1。
假分数:
分子大于或等于分母的分数叫做假分数。
假分数大于或等于1。
带分数:
一个整数(0除外)和一个真分数组合在一起的数,叫做带分数。
百分数(百分率或百分比):
表示一个数是另一个数的百分之几的数。
百分率:
例如:
出勤率,表示出勤的人数占总人数的百分之几。
分 数
百分数
意义
既可以表示数量,又可以表示数量关系.
只表数量关系,不表示数量.
分数后面可以有单位,也可以没有单位.
百分数后面不写单位.
写法
分数的一般写法
专门写法
分数一般要求化简
不必化简
分子不是小数
分子可以是小数
⑶分数和小数的联系:
小数实际上就是分母是10、100、1000……的分数。
小数:
小数是分数的一种特殊形式。
但是不能说小数就是分数。
循环小数:
一个小数,从小数部分的某一位起,一个数字或几个数字依次不断地重复出现,这样的小数叫做循环小数。
依次不断重复出现的数字叫做这个循环小数的循环节。
例如:
3.99……的循环节是“9”,0.5454……的循环节是“54”。
写循环小数的时候,为了简便,小数的循环部分只需写出一个循环节,并在这个循环节的首、末位数字上各点一个圆点。
如果循环节只有一个数字,就只在它的上面点一个点。
有限小数:
小数的小数部分的位数是有限的,这样的小数叫做有限小数。
无限小数:
小数的小数部分的位数是无限的,这样的小数叫做无限小数。
循环小数都是无限小数,无限小数不一定都是循环小数。
例如,圆周率
也是无限小数,它是无限不循环小数。
第2课时:
数的读法、写法、改写及大小比较
知识点一:
计数单位及数位;
整数部分
小数点
小数部分
…
亿级
万级
个级
数位
…
千亿位
百亿位
十亿位
亿位
千万位
百万位
十万位
万
位
千
位
百位
十位
个位
·
十分位
百
分
位
千
分
位
…
计数单位
…
千亿
百亿
十亿
亿
千万
百万
十万
万
千
百
十
一
·
十分之一
百
分
之
一
千
分
之
一
…
…
…
…
…
…
…
…
…
10000
1000
100
10
1
·
…
十进制计数法:
每相邻两个计数单位之间的进率都是10。
这样的计数法叫十进制计数法。
知识点二:
数的读法和写法;
读法要点:
每一级末尾的0都不读出来,每一级的前面或中间连续有几个0都只读一个0。
写法要点:
每一级都只能写四位,不要多写或少写0。
知识点三:
数的改写;
分数能否化成有限小数的判断方法:
一个最简分数分数的分母只有质因数“2或5”,这个分数就能化成有限小数。
如果含有2和5以外的质因数,就不能化成有限小数。
知识点四:
数的大小比较;
第3课时:
分数、小数的基本性质
知识点一:
分数的基本性质;
一个分数的分子、分母同时乘上或除以几(零除外),分数的大小不变。
知识点二:
小数的基本性质;
小数的末尾添上0或去掉0,小数的大小不变,这叫做小数的基本性质。
知识点三:
小数点位置的移动引起小数大小变化的规律;
小数点向右移动一位、二位、三位……原来的数分别扩大10倍、100倍、1000倍……
小数点向左移动一位、二位、三位……原来的数分别缩小10倍、100倍、1000倍……
第4课时:
数的整除
整除:
整数a除以整数b(b≠0),得到的商正好是整数而没有余数,我们就说a能被b整除。
整除与除尽:
整除:
被除数、除数、商都是整数(除数不为0)。
除尽:
整除都可以说是除尽,但除尽不一定是整除。
例如:
l÷5=0.2,叫除尽,不叫整除,因为商是小数。
知识点一:
因数、倍数;
因数和倍数:
当甲数能被乙数整除时,就说甲数是乙数的倍数,乙数是甲数的因数。
如12÷3=4,就说12是3的倍数,3是12的因数。
这两个概念都是相对而存在,一个自然数是不存在是否是倍数或因数的。
例如:
“3是因数”,就是一个错误说法。
只能说3是12的因数,或12的因数有3。
又例如:
“12是倍数”,也是一个错误说法。
只能说12是3的倍数,或3的倍数有12。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
例如:
10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:
3、6、9、12……其中最小的倍数是3,没有最大的倍数。
知识点二:
最大公因数和最小公倍数;
公因数:
几个数公有的因数,叫做公因数。
它的个数是有限的。
最小的公因数是1。
最大公因数:
几个数公有的因数中,最大的一个就叫做这几个数的最大公因数。
公倍数:
几个数公有的倍数。
叫做公倍数。
它的个数是无限的,只有最小的,没有最大的。
最小公倍数:
几个数公有的无限个倍数中,最小的一个就叫做这几个数的最小公倍数。
倍数关系的两个数的最大公因数是小数,最小公倍数是大数;
如果两个数是互质数,那么这两个数的积就是它们的最小公倍数,1是它们的最大公因数。
知识点三:
质数、合数;分解质因数,
质数与合数:
一个数的因数只有1和它本身两个因数的数叫做质数,如2。
一个数的因数除了1和它的本身以外,还有其他的因数,这个数就叫合数,如4。
1既不是质数,也不是合数。
最小的质数是2,最小的合数是4。
质数只有两个因数;而合数至少有三个因数。
质因数:
每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数。
求质因数的过程叫分解质因数。
分解质因数只针对合数。
20以的质数:
235711131719
互质数:
两个数的公因数只有1,而没有其他公因数的,这两个数就叫互质数。
例如9和16,。
以下几种情况的两个数一定是互质数:
⑴、1和其它自然数。
⑵、2和一个奇数。
⑶、两个不相同的质数。
⑷、两个连续的自然数。
⑸、相邻的两个奇数。
⑹、两个数中较大数为质数。
⑺、两个数中的较小数是质数,较大数不是较小数的倍数。
质数与互质数:
质数可以独立存在,而互质数不能独立存在。
比如,8和15是互质数,但不能说“8是互质数”。
知识点四:
2、5、3的倍数的特征;
2的倍数的特征:
个位上是0、2、4、6、8的数是2的倍数。
是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
5的倍数的特征:
个位上是0或5的数是5的倍数。
3的倍数的特征:
一个数的各个数字的和是3的倍数,这个数就是3的倍数。
第二节数的运算
第1课时:
四则运算的意义
知识点一:
四则运算的法则
倒数:
乘积是1的两个数叫做互为倒数。
1的倒数是1,0没有倒数。
常用分数的分数值:
=0.5
知识点二:
四则运算各部分之间的关系
一个数乘以大于1的数,积大于原数;一个数乘以小于1的数,积小于原数;
一个数除以大于1的数,商小于原数;一个数除以小于1的数,商大于原数。
积的变化规律:
一个因数不变,另一个因数乘以几,积就乘以几;另一个因数除以几(0除外),积就除以几。
商不变的性质:
两个数相除,被除数和除数同时乘上或除以几(0除外),商不变(余数的大小有变化)。
当甲×a=乙×b时,如果甲>乙,则a<b;如果甲<乙,则a>b.
知识点三:
0的认识
⑴0的意义:
①0表示没有,比如0个苹果。
②0表示起点,比如尺子,量角器的起点是0,“从0开始”即是从头开始的意思。
③0表示分界,如0是正数和负数的分界点。
④0用来占位,如108中的0表示十位上没有,切不可写作18。
⑵0的性质:
①0是整数,0是偶数,0是最小的自然数。
②0既不是正数也不是负数。
③0没有倒数。
④0不能作除数,分母和比的后项。
a+0=a ;a-0=a;a-a=0;a×0=0;0÷a(a≠0)=0;
a×1=a;a÷1=a;a÷a=1;1÷a=
第2课时:
运算定律与简便算法、四则混合运算;
知识点一:
运算定律与简便算法;
名称
举例
用字母表示
加法交换律
15+28=28+15
a+b=b+a
加法结合律
84+68+32=84+(68+32)
a+b+c=a+(b+c)
连减
257-66-34=257-(66+34)
a-b-c=a-(b+c)
乘法交换律
45×16=16×45
ab=ba
乘法结合律
6×13×5=13×(6×5)
abc=a(bc)
乘法分配律
25×404=25×(400+4)=25×400+25×4
65×37-35×37=37×(65-35)
(a+b)c=ac+bc
或(a—b)c=ac—bc
连除
1200÷25÷4=1200÷(25×4)
a÷b÷c=a÷(b×c)
知识点二:
四则混合运算;
运算法则:
①有括号先算括号里的,先算小括号,再算中括号;
②两级运算,先算乘除,后算加减;
③同级运算,从左到右;
第三节式与方程
知识点一:
用字母表示数;
知识点二:
简易方程
方程:
含有未知数的等式叫做方程。
(注意:
不是“含有未知数的式子叫方程”)
第四节解决问题
第1课时:
整数、小数应用题
1、每份数×份数=总数
2、1倍数×倍数=几倍数
3、速度×时间=路程
4、单价×数量=总价
5、工作效率×工作时间=工作总量
6、加数+加数=和
7、被减数-减数=差
8、因数×因数=积
9、被除数÷除数=商
第2课时:
分数、百分数应用题
1、单位“1”×数量关系=数量数量÷数量关系=单位“1
注意:
⑴、单位“1”一般在“的”前面,“比”或“占”后面;
⑵、分数乘除法应用题中,如果所列数量关系是乘法,一般是用单位“1”作开头。
⑶、“数量”和“数量关系”必须是对应的;
2、甲÷乙=甲是乙的几分之几(或百分之几)
如果甲是乙的
,那么甲有a份,乙有b份
3、差÷单位“1”=多(少)几分之几
如果甲比乙多(少)
,那么乙有b份,甲乙之差为a份
4、发芽率=发芽种子数÷试验种子数×100%
小麦的出粉率= 面粉的重量÷小麦的重量×100%
产品的合格率=合格的产品数÷产品总数×100%
职工的出勤率=实际出勤人数÷应出勤人数×100%
5、本金×利率×时间=利息
第五节常见的量
知识点一:
常见的计量单位;
知识点二:
名数的改写;
第六节比和比例
知识点一:
比的意义、性质、化简比和求比值;
比:
两个数相除,又叫做两个数的比。
比的基本性质:
在比的前项和后项同时乘上或除以相同的数(0除外),比值不变。
比值:
比的前项除以后项所得的商,叫做比值。
比值不带单位名称。
化简比和求比值:
前者的结果是一个比——a:
b或
(即分数形式的比),
后者的结果是一个数(整数、小数或分数)。
知识点二:
比例的意义和性质;
比例的基本性质:
在比例里,两个外项的积等于两个项的积。
当甲×a=乙×b时,甲÷乙=b÷a;乙÷甲=a÷b。
知识点三:
比例尺、正比例和反比例;13%,
图上距离:
实际距离=比例尺
第二章空间与图形
第一节图形的认识与测量
第1课时:
图形的认识与测量⑴
知识点一:
直线、射线、线段;
类型
端点
延伸
测量
图形
共同点
直线
无端点
向两端无限延伸
不可测量
—————
都是直直的
射线
1个
向一端无限延伸
不可测量
●————
线段
2个
不延伸
可测量
●————●
直线的性质:
两点确定一条直线。
线段的性质:
两点间,线段最短。
直线和射线无法比较长短。
射线和线段都是直线的一部分。
知识点二:
角的分类及性质;
角:
从一点引出两条射线所组成的图形叫做角。
角的分类:
角的大小比较:
角的大小与角的两边画出的长短没关系。
角的大小要看两条边叉开的大小,叉开得越大,角越大。
知识点三:
垂直与平行;
平行线:
在同一平面不相交的两条直线叫做平行线。
平行线的性质:
平行线间,垂线段最短。
垂线、垂足:
两条直线相交,有一个角是直角时,就说这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线,其交点叫垂足。
点到直线的距离:
从直线外一点向一条直线引垂线,点和垂足之间的距离叫做这点到直线的距离。
点到直线之间,垂线段最短。
第2课时:
图形的认识与测量⑵
知识点一:
三角形;
三角形:
由三条线段围成的图形叫三角形。
锐角三角形:
三个角都是锐角的三角形叫锐角三角形。
直角三角形:
有一个角是直角的三角形叫直角三角形。
钝角三角形:
有一个角是钝角的三角形叫钝角三角形。
等腰三角形:
两条边相等的三角形叫等腰三角形。
等边三角形:
三条边都相等的三角形叫等边三角形,也叫正三角形。
三角形的高和底:
从三角形的一个顶点向它的对边引一条垂线,顶点和垂足之间的线段叫做三角形的高,这个顶点的对边叫三角形的底。
三角形只有3条高。
三角形角和:
180°.
三角形具有稳定性。
每个三角形都至少有两个锐角,至多有1个直角,至多有1个钝角。
知识点二:
四边形;
平行四边形容易变形,它不具有稳定性。
知识点三:
圆
直径:
通过圆心,并且两端都在圆上的线段叫做圆的直径。
半径:
连接圆心和圆上任意一点的线段,叫做圆的半径。
圆的直径和半径都有无数条。
圆是轴对称图形,每条直径所在的直线是圆的对称轴。
圆的半径或直径决定圆的大小,圆心决定圆的位置。
圆周率:
周长:
直径=圆周率。
完美的圆形:
面积相等的几何图形中,圆的周长最短;长度相等的几何图形中,圆的面积最大。
第3课时:
平面图形的周长和面积
知识点一:
平面图形的周长;
知识点二:
平面图形的面积;
常用圆周率倍数值:
3.14×2=6.283.14×3=9.423.14×4=12.563.14×5=15.7
3.14×6=18.843.14×7=21.983.14×8=25.123.14×9=28.26
常用平方:
112=121122=144132=169142=196152=225162=256172=289182=324192=361252=625
第4课时:
立体图形
知识点一:
立体图形的认识;
相同点
不同点
面
棱
长方体
都有6个面,
12条棱,
8个顶点。
6个面都是长方形。
(有可能有两个相对的面是正方形)。
相对的棱的长度都相等
正方体
6个面都是正方形。
12条棱都相等。
站在任一位置都不能同时看到长方体所有的面,最多只能看到它的三个面。
知识点二:
立体图形的表面积和体积;
体积和容积(容量):
体积从外面测量数据,容积从里面测量数据。
名称
棱长和
表面积
体积
长方体
棱长和=(长+宽+高)×4
S长=2(ab+ah+bh)
统一公式:
侧面积+底面积×2
V正=a3
统一公式:
V=Sh
正方体
棱长和=棱长×12
S正=6a2
V正=a3
圆柱体
表面积=侧面积+底面积×2
V圆柱=Sh
空心圆柱
V空=V外-V
圆锥体
V圆锥=
Sh
第二节图形与变换
知识点一:
轴对称图形;
轴对称图形:
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
画对称轴时,要画虚线,而且要两边出头(因为对称轴是一条直线)。
知识点二:
平移和旋转;
平移:
物体或图形平移后本身的形状、大小和方向都不会改变。
旋转:
只改变物体的位置(旋转中心位置不会变),不改变物体的形状、大小。
知识点三:
图形的放大与缩小;
放大和缩小:
只改变物体的大小,不改变物体的形状。
第三节图形与位置
知识点一:
根据示意图描述物体的位置;
知识点二:
根据描述画出物体的位置;
知识点三:
使用路线图;
数对:
用数对表示位置时,第一个数表示列,第二个数表示行。
第三章统计与概率
知识点一:
统计表和统计图;
条形统计图的特点:
可以清楚地表示出各种数量的多少。
折形统计图的特点:
不但可以表示出各种数量的多少,还可以清楚地看出各种数量的增减变化情况。
扇形统计图的特点:
可以清楚地表示出各部分和总体之间的关系。
知识点二:
平均数、中位数和众数;
平均数:
一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
平均数容易受极端数据的影响,表示一组数据的平均情况。
总数÷总份数=平均数
中位数:
将一组数据按大小顺序排列,处在最中间位置的“一”个数叫做这组数据的中位数。
它不受极端数据的影响,表示一组数据的一般情况。
众数:
在一组数据中出现次数最多的数叫做这组数据的众数。
它不受极端数据的影响,表示一组数据的集中情况。
知识点三:
可能性;
第四章数学广角
知识点一:
植树问题;
知识点二:
编码
邮政编码:
由六位数字组成,前两位数字表示省(或自治区、直辖市);第三位数表示邮区;第四位数表示县(市);最后两位数表示投递局(所)。
居民:
18位
13 05 21 19780301 001 9
省 市 县 出生日期 顺序码 校验码
倒数第二位的数字用来表示性别,单数表示男,双数表示女。
知识点三:
找次品
找次品优化策略:
把物品分成3份,尽量平均分,可以保证找出次品而且称的次数一定最少。
高频考点:
1、脱式计算(偏重简算)
2、比和比例(偏重)
3、应用题(包括整数、小数应用题和分数百分数应用题)
4、立体图形的表面积和体积;
零星高频考点:
1、数的改写;
2、分解质因数;
3、图形与位置
4、复杂的折线图
中频考点:
数的意义;数的整除;计算;解方程;平面图形的面积;
比重较低考点(1、2分):
数的读写法;2、5、3倍数的特征;圆;平面图形;图形与变换;统计与概率;
非考点:
计数单位及数位;数的大小比较;四则运算各部分之间的关系;0的认识;用字母表示数;常见的量;直线射线线段;角;垂直与平行;三角形;四边形;立体图形的认识;图形的放大与缩小;使用路线图;统计图表;平均数,中位数,众数;数学广角;