SPSS重复测量方差分析例题答案.docx
《SPSS重复测量方差分析例题答案.docx》由会员分享,可在线阅读,更多相关《SPSS重复测量方差分析例题答案.docx(16页珍藏版)》请在冰豆网上搜索。
SPSS重复测量方差分析例题答案
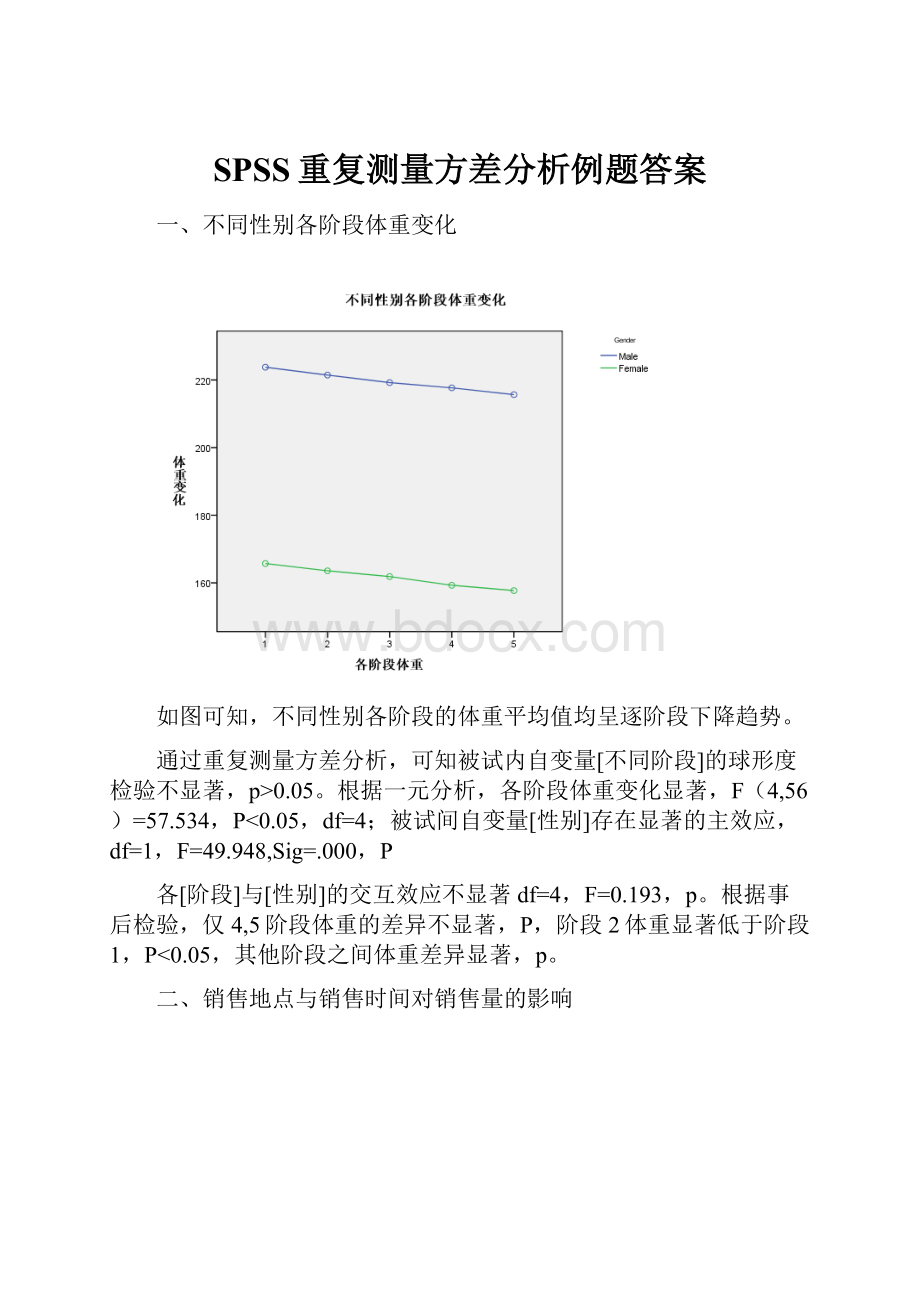
一、不同性别各阶段体重变化
如图可知,不同性别各阶段的体重平均值均呈逐阶段下降趋势。
通过重复测量方差分析,可知被试内自变量[不同阶段]的球形度检验不显著,p>0.05。
根据一元分析,各阶段体重变化显著,F(4,56)=57.534,P<0.05,df=4;被试间自变量[性别]存在显著的主效应,df=1,F=49.948,Sig=.000,P
各[阶段]与[性别]的交互效应不显著df=4,F=0.193,p。
根据事后检验,仅4,5阶段体重的差异不显著,P,阶段2体重显著低于阶段1,P<0.05,其他阶段之间体重差异显著,p。
二、销售地点与销售时间对销售量的影响
根据重复测量方差分析,被试内自变量[销售时间]的球形度检验显著df=2,p1,根据多元分析,可知[销售时间]和[地区]的交互效应显著,F=5.590,p。
被试间自变量[地区]对销售时间的影响显著,df=2,F=58.149,Sig=。
000,P<0.01。
由于交互作用显著,现作简单效应分析:
①同一销售时间,不同地区
表1:
同一销售时间不同地区的销售量单因素方差分析
齐性检验
方差分析
df1
Sig
df
MS
F
Sig
销售时间1
2
.790
2
.000**
销售时间2
2
.205
2
49,741
.000**
销售时间3
2
.722
2
.000**
**p<0.01
由表可得,在同一销售时间(1或2或3)中,不同地区的销售量均差异显著,p<0.01,即自变量[地区]对[销售量]存在显著的主效应。
在事后检验中,不同地区的销售量均差异显著,p<0。
01,呈现地区1销售量>地区2销售量>地区3销售量。
②同一地区,不同销售时间
表2:
同一地区内不同销售时间的销售量重复测量方差分析
球形度检验
一元分析/多元分析
df
Sig
df
MS
F
Sig
地区1
2
.731
2
.000**
error1
10
地区2
2
.332
2
.000**
error2
10
地区3
2
.064
2
.010*
error3
10
*p<0.05;**p
由此可知,同一地区不同销售时间下,销售量存在显著差异,即自变量[销售时间]对[销售量]存在显著主效应。
同时,根据事后检验,在三个地区中,销售时间2的销售量均显著高于销售时间1和销售时间3,p<0.01;在地区1中,销售时间1的销售量显著高于销售时间3,p<0.05,在地区2和3中,销售时间1与3的销售量则无显著差异,p>0.05。
《SPSS原理与运用》练习题
数据对应关系:
06-均值检验;07-方差分析;08-相关分析;
09-回归分析;10-非参数检验;17-作图
1、以data06-03为例,分析身高大于等于155cm的与身高小于155cm的两组男生的体重和肺活量均值是否有显著性。
分析:
一个因素有2个水平用独立样本t检验,此题即身高因素有155以上和以下2个水平,因此用独立样本t检验(analyze->comparemeans->independent-samplesTtest)。
报告:
一、体重①m+s:
>=155cm时,m=40.838kg;s=5.117;
<155cm时,m=;s=3.816;
②方差齐性检验结果:
P=0.198>0.05,说明方差齐性。
③,说明身高大于等于155cm的与身高小于155cm的两组男生的体重有极显著性差异。
二、肺活量①m+s:
>=155cm时,m=2.404;s=0.402;
<155cm时,m=2.016;s=0.423;
②方差齐性检验结果:
P=0.961>0.05,说明方差齐性。
③t=2.512;p=0.018,说明说明身高大于等于155cm的与身高小于155cm的两组男生的体重有显著性差异。
2、以data06-04为例,判断体育疗法对降低血压是否有效。
分析:
比较前后2种情况有无显著差异,用配对样本t检验,(analyze->comparemeans->paired-samplesTtest).
报告:
①m+s治疗前舒展压:
m=119.50;s=10.069;
治疗后舒展压:
m=102.50;s=11.118;
②相关系数correlation=0.599;p=0.067>0.05,说明体育疗法与降低血压相关。
③t=5.639;p=0.001<0.05,说明体育疗法对降低血压有效。
3、以data07-01为例,比较四种饲料对猪体重增加的作用有无不同。
分析:
一个因素多个水平用单因素方差分析。
(analyze->comparemeans->One-wayANOVA)。
操作中,contrast不用改;post-hoc中需勾Bonferroni和S-N-K;Options中需勾第1个descriptive和第3个Homegeneityofvariancetest.
报告:
①m+s:
A:
m=133.36;s=6.808;B:
m=152.04;s=6.957;
C:
m=189.72;s=6.350;D:
m=220.78;s=6.106;
②方差齐性检验结果:
F=0.024;P=0.995>0.05,说明方差齐性。
③F=157.467;p=0.001,说明ABCD四种饲料对猪体重增加的作用有显著性差异。
④POST-HOC检验表明:
ABCD四种饲料对猪体重增加的作用效果从高到低依次为:
D>C>B>A.(如何看图及如何排序,方法:
如表格中显示D-A=87.415;D-B=68.735;D-C=31.055,假设D=100,则易可计算出ABC的假设值,再根据假设值对ABCD进行排序即可)
4、以data07-10为例,分析四种药物对某生化指标有无显著性作用。
分析:
对一个样本重复测量时,作重复测量方差分析。
(analyze->generallinearmodel->repeatedmeasure)
操作:
一、定义:
factorname中填med;numberoflevels中填4;->add->define:
将四个指标一起添加到第一个框中去—》options中3个必要操作:
1将med选到右边框中去,2勾选下边的comparemaineffect,在confidentintervaladjustment复选框中选Bonferroni;3desplay框中选第1个Des…和第2个Esti..。
->OK
报告:
看结果时看第一个表descriptvestatics和第5个表testofwithin-subjectseffects表中的greenhouse-geisser结果F和Sig(即稍后要报告的p)即可
①m+s:
服药1后生化指标:
m=26.40;s=8.764;
服药2后生化指标:
m=15.60;s=6.542;
服药3后生化指标:
m=15.60;s=3.847;
服药4后生化指标:
m=32.00;s=8.000.
②F=24.759,p=0.001<0.01,说明差异显著,四种药物对某生化指标有显著性作用。
且其中药物4所起的作用最大,药物3所起的作用最大小(据平均值可看出来)。
5、以data08-01为例,分析国民收入与城乡居民储蓄存款余额之间的关系。
分析:
变量间不准确不稳定的变化关系称之为相关关系。
相关分析种类很多,spss中有二列相关(Bivariate)、偏相关(partial)、距离分析(distances)3类。
其中的二列相关分析(Bivariate)有3种:
⑴Pearson皮尔逊相关系数,即积差相关:
就是2个变量标准分数乘积的算术平均数,它用于两个变量都是连续型变量时;
⑵Kendall’stau-b:
即肯德尔和谐系数,用于2(/3个以上)变量都是离散型变量时,可检验多个被试是否具有一致性。
它分单维和双维。
⑶Speaman斯皮尔曼等级相关:
用于两变量中有1个是离散型变量时。
操作:
Analyze—>Correlate—>Bivariate(此题符合Pearson相关)
1)Variables:
选入这两个变量
2)Options:
勾选Meansandstandarddeviations即可。
报告:
①m+s国民收入m=128.5452,其S=;
城乡居民储蓄存款m=14.1216,s=。
②**,相关极显著,且成正相关。
6、以data08-03为例,判断树木的月生长量与月平均气温、月降雨量、月平均日照时数、月平均湿度这4个气候因素的关系。
分析:
此题用偏相关partial,偏相关用于分析事物间是否存在潜在的关系。
但作偏相关都首先需作一般相关。
操作:
第一步:
二列相关
Analyze—>Correlate—>Bivariate(Pearson相关)
1)variables:
选入所有变量
2)option:
Meansandstandarddeviations前打钩。
报告:
①5个变量的平均数和标准差:
m+s(见截图)
②树木的月生长量与四个因子相关系数分别为:
(看有无*,看*有多少)
**,相关极显著,成正相关。
**,相关极显著,成正相关。
*,相关显著,成正相关。
相关系数r=0.374,无显著相关。
第二步:
偏相关
Analyze—>Correlate—>Paritable(Pearson相关)
1)Variables:
树木的月生长量与月平均气温;
2)Controllingfor:
月降雨量、月平均日照时数、月平均湿度
做其它两者之间的关系,操作类似,只是有点麻烦。
报告:
r=0.977,其他因素对树木的月生长量与月平均气温之间的关系有影响;r=-0.491,…有影响;r=0.632,…有影响。
(因为树木的月生长量与月平均湿度之间无显著相关,就没必要再做偏相关)
7、以data02-01为例,建立一个以初始工资、工作经验、受教育年数为自变量,当前工资为因变量的回归方程。
分析:
回归表示一个变量随另一个变量作不同程度变化的单向关系。
根据自变量的多少克可分为一元回归分析与多元回归分析。
过程:
先做散点图,判断是用线性回归还是曲线回归(一般用线性回归)
操作:
一、打开data,选择REGRESSION——linearregression,选择因变量、自变量。
二、在method中选择stepwise
三、在statistics中增加选项Rsquaredchange,descriptive
报告:
①目前工资的平均值是...,标准差是...
初始工资的平均值是...,标准差是..
工作经验的平均值是...,标准差是...
教育年数的平均值是...,标准差是...
DescriptiveStatistics
DescriptiveStatistics
Mean
Std.Deviation
N
CurrentSalary
474
BeginningSalary
474
EducationalLevel(years)
474
MonthssinceHire
474
②.解释力度为0.80,解释力度很大.
ModelSummary
Model
R
RSquare
AdjustedRSquare
Std.ErroroftheEstimate
ChangeStatistics
RSquareChange
FChange
df1
df2
Sig.FChange
1
.880(a)
.775
.774
.775
1
472
.000
2
.890(b)
.792
.792
.018
1
471
.000
3
.895(c)
.801
.800
.008
1
470
.000
Coefficients(a)
1
(Constant)
.031
BeginningSalary
.047
.880
.000
2
(Constant)
.000
BeginningSalary
.059
.771
.000
EducationalLevel(years)
.172
.000
3
(Constant)
2
.000
BeginningSalary
.058
.779
.000
EducationalLevel(years)
.163
.000
MonthssinceHire
.092
.000
aDependentVariable:
CurrentSalary
③回归方程:
Y^=—19986.5+1.689*beginingsalary+966.107*educationallevel+155.701*monthssinceHire
8、掷一颗六面题300次,见data10-01a,问这颗六面体是否均匀?
分析:
X2卡方是检验实际频数与理论频数之间差异的统计量。
6面体如果均匀的话,6个面出现的频数应该是无显著差异。
操作:
Analyse—NonparametricTests—Chi—square(卡方检验)
将Imt加入到TestVariableList里
Options——勾选Descriptive
报告>0.05,说明无显著性差异,
所以,这颗六面体均匀。
9、某研究者就目前就业情况作调查,在68名男性大学生中,39人认为“很好”,29人认为“不好”,在57名女性大学生中,42人认为“不好”,15人认为“很好”,试问大学生的态度是否与其性别有关?
分析:
原理同上题,理论值和实测值如果有显著性差异,则与其有关,若无显著性差异,则无关。
操作:
创建表:
定义变量gender,attitude,num,输入数据
Data——weightcase——num
选择descriptivestatistics——crosstabs
ROW——gender,COLUMN——attidtude
STATISTICS中选择chi_squareCELLDISPLAY中增加选项COUNTS:
EXPECTED
报告:
①;
;
女性认为很好的实测值有15人,期望值为人;
女性认为不好的实测值有42人,期望值是3人。
②卡方检验结果:
x2=12.173,P=0.001<0.01,表明学生态度受性别影响。
(看第一行PearsonChi-square那一行中的值)
10、有甲、乙两种药物,独立观察20名患者,其中10人各服甲、乙药物,试比较两种药物的疗效是否不同,数据见data10-06。
分析:
本题采用非参数检验。
假设检验的方法有参数检验和非参数检验2种。
参数检验是根据样本信息对相应的总体参数的假设检验。
它对数据要求高,如总体呈正态或近正态分布。
但实际研究中出现总体状态不明,或总体状态呈非正态分布时,此时可采用非参数检验。
操作1)analyse—NonparametricTest—2Independentsamplestest;
2)将ycss加入testvariablelist框中,将zb加入grooupingvariable中,在definegroup中定义分组;(在group中分别输入1、2)
3testtype中四个选项全选,option中选择descriptive
报告:
①m+s:
ycss:
m=1.625;s=;
Zb:
m=1.50;s=;
②四种检验的P值如下:
1)Mann-WhitneyTest检验:
<0.05表明差异显著.
P2=0.035<0.05表明差异显著。
2)Moses-Test检验有2个P值,不显著;,表明差异不显著。
3),表明差异不显著。
4)表明差异显著。
表明差异不显著。
综合以上各种检验的P值来看,这两种药物之间的疗效差异不显著。
11、以data17-01数据文件生成1985-1994年某个城市12个月份平均气温的简单条形图。
第11题:
以data17-01数据文件生成1985-1994年某个城市12个月份平均气温的简单条形图。
操作:
1.题目分析:
因为只有一个城市,所以用简单的画图
2.Graphs-bar(选第一个sample)
3.圆坨坨选最后一个otherstatistic把北京选入第一个框框variable将月份选入第二个框框categoryaxis
结果:
这是以北京市的情况为例的。
12、以data17-07数据文件为例,分别生成1993年俄罗斯每季度失业人口情况和部分独联体国家失业人口情况的圆图。
步骤:
题目分析:
本题有两问
1.1993年俄罗斯每季度失业人口情况,因为只有一个国家,所以用简单的画图
2.Graphs-pie(选第一个sample)
3.圆坨坨选最后一个otherstatistic把俄罗斯选入第一个框框variable将季节选入第二个框框defineslices
这是第一问,俄罗斯的情况
1.部分独联体国家失业人口情况的圆图,因为只有一个国家,所以用第二个画图2.Graphs-pie(选第二个separate)
3.把部分独联体国家选入第一个大框框slicesrepresent
Unit1
1.SPSSforWindows软件有几种运行方式?
什么是混合运行方式,它有什么特点?
2.SPSSforWindows有几种类型的窗口,每个窗口主要功能是什么?
答:
3种,数据窗口(处理数据);结果窗口(显示结果);语句窗口(用来编程)
3.什么是输出窗(或语句窗)的主窗,什么是主窗的标志?
怎样把非主窗变成主窗?
分出主窗和非主窗的作用是什么?
以输出窗为例说明之。
4.通过什么菜单项设置系统参数?
Edit中的Options
5.SPSS的统计分析功能分布在何处?
Analyze
6.从何处可以获得帮助信息?
系统提供的帮助有几种形式?
7种:
Topics;Tutorial;StatisticsCoach;对话框中的右键帮助;选择项的右键帮助;输出项的右键帮助;统计量解释的右键帮助
Unit4
1.均值比较的T检验分几种类型?
各自检验的假设是什么?
单一样本t检验,检验单个变量的均值是否与给定的常数之间存在差异。
即样本均值与总体均值相等的假设。
两个独立样本的t检验用于检验两个不相关的样本来自具有相同均值的总体。
配对样本t检验(PairedSampleTtest)用于检验两个相关的样本是否来自具有相同均值的总体。
2.要使用T检验进行均值比较的变量,应该具有怎样的分布特征?
变量应该是正态分布的。
如果分析变量明显是非正态分布的,应该选择非参数检验过程。
3.独立样本T检验对变量的齐性有什么要求?
被检验的两个样本方差要求具有齐性,如果不齐,使用校正公式计算T值和自由度。
因此,在输出结果中,应该先检查方差齐性,根据齐性的结果,在输出表格中选择T检验的结果。
Unit5
1.简述方差分析的基本思想。
用简单的表达式表示单因素方差分析的偏差平方和分解。
通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
2.方差分析的假定的前提条件有哪些?
(1)各处理条件下的样本是随机的。
(2)样本是相互独立的,否则可能出现无法解析的输出结果。
(3样本分别来自正态分布总体,否则使用非参数分析。
(4)方差齐性。
3.什么是主效应?
什么是交互效应?
一个因素的水平之间的平均数差异,称为该因素的主效应。
当研究设计被呈现为一个矩阵,并且第一个因素定义行,第二个因素定义列的时候,行与行之间的平均数差异描述就是第一个因素的主效应,列之间的平均数差异描述的是第二个因素的主效应
当被试处理情境之间或单元之间的平均数差异显著不同于因素的全部主效应时,双因素之间的交互作用就发生了。
或者可以这样理解,当双因素实验研究的结果以图形呈现的时候,如果存在不平行的折线,则说明存在交互作用
4.简述协方差分析的基本思想。