导数与恒成立能成立问题.docx

导数与恒成立能成立问题.docx

《导数与恒成立能成立问题.docx》由会员分享，可在线阅读，更多相关《导数与恒成立能成立问题.docx（24页珍藏版）》请在冰豆网上搜索。

导数与恒成立能成立问题

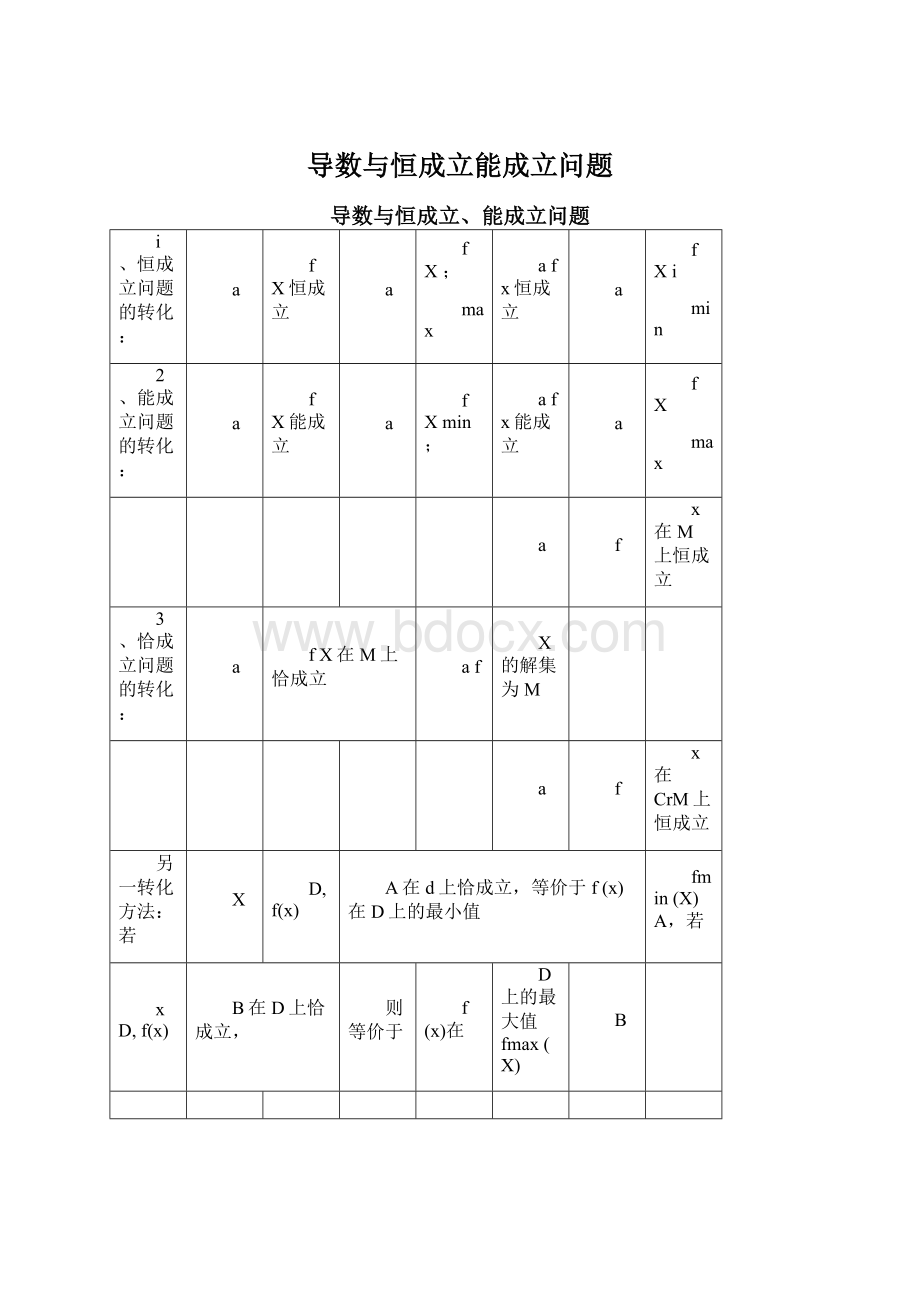
导数与恒成立、能成立问题

i、恒成立问题的转化：

a

fX恒成立

a

fX；

max

afx恒成立

a

fXi

min

2、能成立问题的转化：

a

fX能成立

a

fXmin；

afx能成立

a

fX

max

a

f

x在M上恒成立

3、恰成立问题的转化：

a

fX在M上恰成立

af

X的解集为M

a

f

x在CrM上恒成立

另一转化方法：

若

X

D,f（x）

A在d上恰成立，等价于f（x）在D上的最小值

fmin（X）A，若

xD,f（x）

B在D上恰成立，

则等价于

f（x）在

D上的最大值fmax（X）

B

设函数fx

，对任意的

Xi

，存在

c,d，使得f

Xi

X2，则fmi

min

gminX

设函数fx

，对任意的

Xi

，存在

X2

c,d，使得f

Xi

X2

，则fmax

gmaxX

设函数fX

，存在Xi

b，存在X2

c,d，使得fx

X2

，则fmax

gmin

设函数fX

，存在Xi

b，存在X2

c,d，使得fxi

X2

，则fmin

gmax

若不等式f

X在区间

上恒成立，等价于在区间D上函数yfx

和图象在函数y

X图象上方;

9、若不等式fX

gX在区间D上恒成立，等价于在区间D上函数y

X和图象在函数ygx图象下方;

导数专题恒成立、能成立问题专题经典题型

题型一、简单型

2a

例1、已知函数f（x）x2ax1,g（x），其中a0,x0.

x

i）对任意x［1,2］，都有f（x）g（x）恒成立，求实数a的取值范围；（构造新函数）

2）对任意x1［1,2］,x2［2,4］，都有f（x1）g（x2）恒成立，求实数a的取值范围；（转化）

ai1

例2、设函数h（x）xb，对任意a［丄，2］，都有h（x）10在x［上，1］恒成立，求实数b的范围.

x24

x

21

例3、已知两函数f（x）x2，g（x）m，对任意X10,2，存在X21,2，使得f（刘）gX2，则实数m

2

的取值范围为

题型二、更换主元和换元法

例1、已知函数f（x）ln（exa）（a为常数）是实数集R上的奇函数，函数gxf（x）sinx是区间1,1上的减函数，

（I）求a的值；

（n）若g（x）t2t1在x1,1上恒成立，求t的取值范围；

例2、已知二次函数

f（x）ax2

x1对x0,2恒有

f（x）

0，求a的取值范围。

例3、对于满足0

a4的所有实数

a求使不等式x2ax

4x

a3都成立的x的取值范围

题型三、分离参数法（欲求某个参数的范围，就把这个参数分离出来）

此类问题可把要求的参变量分离出来，单独放在不等式的一侧，将另一侧看成新函数，于是将问题转化成新函数的最值问题：

若对于x取值范围内的任一个数都有f（x）g（a）恒成立，贝Ug（a）f（x）min；若对于x取值范围内的任一个数都有f（x）g（a）恒成立，则g（a）f（x）max.

2

例1、当x1,2时，不等式xmx40恒成立，则m的取值范围是,

x2

例2、已知函数f（x）ln（ea）（a为常数）是实数集R上的奇函数，函数g（x）xcosx在区间——上是减函数.

3'3

（I）求a的值与的范围；

题型四、数形结合（恒成立问题与二次函数联系（零点、根的分布法））

，、‘2丄

（H）若对（I）中的任意实数

都有g（x）t1在，上恒成立，求实数t的取值范围.

33

利用不等式性质

利用分类讨论

利用导数迂回处理

a

例3、已知函数f（x）x（lnxm）,g（x）xx.

（I）当m2时，求f（x）的单调区间;

3

（且）若m时，不等式g（x）f（x）恒成立，求实数a的取值范围.

注：

恒成立问题多与参数的取值范围问题联系在一起，是近几年高考的一个热门题型，往往与函数的单调性、极值、最值等有关。

小结：

恒成立与有解的区别:

1不等式fx

2不等式fx

3不等式fx

4不等式fx

M对xI时恒成立

M对xI时有解

M对xI时恒成立

M对xI时有解

fmax（X）M?

xI。

即f

fmin（X）M?

，xI

fmin（x）M?

，xI。

即f

fmax（x）M，xI.。

或f

x的上界小于或等于M;x的下界小于或等于M；

x的下界大于或等于M;

x的上界大于或等于M;

导数专题恒成立、能成立问题专题经典题型答案

例1简解：

（1）由x22ax

a

1-

x

0a

x3

2x2

x

成立，只需满足（x）

1

3x

2x2

x

1

的最小值大于

a即可.对

3

（x）x2x求导，（x）2x21

2x4

（2x2

x21

1）2

0，故

（x）在x[1,2]是增函数，

min

（x）

2

（1）3

，所以a的取

题型一、简单型

值范围是0a2-

3

方法1：

化归最值，h（x）

10

hmax（x）

10；

方法2:

变量分离，b10

（a

x）或a

x2（10

b）x；

x

方法3:

变更主元（新函数），

（a）

1

ax

b10

0,a

1

H,2］

x

2

简解：

方法1：

对_

求导，h（x）

1a（x

12

a）（x

2

a），（单调函数）

h（x）-

xb

x

x

例2分析：

思路、解决双参数问题一般是先解决一个参数，再处理另一个参数.以本题为例，实质还是通过函数求最值解决.

由此可知,

h

（1）

4

h

（1）

x

11

h（x）在［-,1］上的最大值为h（—）与h

（1）中的较大者.4''

1

4a—b10

4

1ab10

10

10

例3答案：

m

题型二、更换主元和换元法

4

39,

4a1

4，对于任意a[—,2]，得b的取值范围是b

9a2

例1（H）分析：

在不等式中出现了两个字母:

及t,关键在于该把哪个字母看成是一个变量，另一个作为常数。

显然可将

视作自变量，则

上述问题即可转化为在

，1内关于的一次函数大于等于0恒成立的问题。

（H）略解：

由（I）知:

f（x）x,g（x）

sinx,Qg（x）

在11上单调递减,

g（x）

cosx0

COSX在1，1上恒成立,

1,g（x）max

g

（1）

sin1，

只需

sin1t2t1,

（t1）

t2sin11

0（其中

1）恒成立，由上述②结论：

可令f

（t1）t2

sin1

10（

1）,

t10

1t2sin11

t1

t2tsin10

，而t2t

sin10恒成立,

例2解:

2

对x0,2恒有f（x）0即axx1

0变形为ax

（x1）

0时对任意的a都满足f（x）0只须考虑x

0的情况

1

现求-

x

（x1）即

2即a

x

1在

2在x

x

0,2

1

要满足题意只要保证a

x

比右边的最大值大就行。

g（t）max

g

（2）

又f（x）

ax2

例3答案:

上的最大值。

令t

所以a

g（t）t2t

（t

（t

1是二次函数

0所以a

题型三、分离参数法（欲求某个参数的范围，就把这个参数分离出来）

例1解析：

当x（1,2）时，由x2

mx

x2

例2解：

（I）、（皿）略

（H）由题意知,

函数g（x）

COSX在区间

—上是减函数.

3

g（x）max

g（3）3

2，g（x）t

上恒成立

t3r（Q

1）

题型四、数形结合（恒成立问题与二次函数联系（零点、根的分布法）

例1解析:

x

R,不等式|x|

ax

对x

ax恒成立、则由一次函数性质及图像知

1。

例2解：

画出两个凼数yax和y•.x（4x）在x[0,3]上的图象

如图

知当x3时y3，

.J3

［0,3］时总有ax.x（4x）所以a-—3

x

ax

例3解：

在同一个平面直角坐标系中分别作出函数y2xm及y

f（x）的图象，由于不等式

f（x）2x

函数y2xm的图象应总在函数y

f（x）的图象下方,

因此，当

2时，y4m

0,所以m

m恒成立，所以

4,故m的取值

范围是4,

题型五、其它（最值）处理方法

例1解：

设fx

2

a3a有解,

a23a

xmin

4，二a23a4，解得

例2解：

由题意知只须

x3的最小值相同或比其最小值小即可，得a（x

3）min

（x

3）

5所以a5

利用分类讨论

所以必须考察a与-1，2的大小，显然要进行三种分类讨论

1）.当a2时f（x）在［-1，2］上是减函数此时f（X）mjn=f

（2）=4-4a+42

即a-结合a2，所以a2

2

f（x）min=f（-1）=1+2a+4

2结合a

x22a2

3）.当-1

所以2a

综上1，2，3满足条件的a的范围为：

a3或a、.2

2

利用导数迂回处理

例1解：

f（x）g（x）在［0,1］上恒成立，即,x12xt0在［0,1］上恒成立

即、x12xt

0在［0,1］上的最大值小于或等于0

令F（x）x1

2xt所以

'1

F（x）麺

214x1，又x

2Jx1

[0,1]所以F（x）

0即F（x）在［0，1］上单调递减

所以F（x）max

F（0），即F（x）F（0）1

例2解:

因为函数

x存在单调递减区间，所以f

ax

（n）

3时，不等式g（x）

即ax2

3

Inx

13（lnx

，所以a2

2x

a3f（x）即x

3

2）丄.令h（x）

xx（ln

3（lnx

2x

3一

）恒成立.由于x

2

1）

26lnx

2，则h（x）—

x

-x21

3

3

Inx，亦

2

，由h（x）0得x1.且当

1时，h（x）0;当x1时，h（x）0，即h（x）在（0,1）上单调递增，在（1,

）上单调递减，所以h（x）在x1

处取得极大值h

（1）3，也就是函数h（x）在定义域上的最大值.因此要使a

2

1

3（lnx-）厂厶恒成立，需要a

x

-，所以a的取值范

2

围为

例3解：

（I）略

导数专题恒成立、能成立问题专题针对性练习

232

1、已知两函数fx7x28xc,gx2x4x40x。

（1）对任意x3,3，都有fxgx）成立，求实数c的取值范围；

（2）存在x3,3，使fxgx成立，求实数c的取值范围；

（3）对任意Xi,X23,3，都有fXigX2，求实数c的取值范围;

（4）存在x,k3,3，都有fXigX2，求实数c的取值范围;

2、设a1,若对于任意的x[a,2a]，都有y[a,a2]满足方程logaxlogay3，这时a的取值集合为（）

5、不等式axJx4x在x0,3内恒成立，求实数a的取值范围。

1322

6、设函数f（x）x2ax3axb（0a1,bR）.

3

（I）求函数fx的单调区间和极值；

（且）若对任意的x[a1,a2],不等式fxa成立，求a的取值范围。

7、已知A、B、C是直线上的三点，向量oA，OB，OC满足：

OAy2f1OBInX1OC0.

（1）求函数y=f（x）的表达式；

2x

（2）若x>0，证明：

f（x）>x+2；

（3）若不等式-x2fx2m22bm3时，x1,1及b1,1都恒成立，求实数m的取值范围.

2

8、设fxpxq2lnx，且feqep2（e为自然对数的底数）

xe

⑴求p与q的关系;

（II）若fX在其定义域内为单调函数，求p的取值范围;

（iii）设gx

2e

，若在1,e上至少存在一点x0，使得fx0gx0成立，求实数p的取值范围.

X

导数专题恒成立、能成立问题专题针对性练习答案

函数的自变量不同，X1，X2的取值在3,3上具有任意性，a要使不等式恒成立的充要条件是:

fmax（X）

gmin（X）,?

?

X

[3,3]o

hmaxXc70，于是得c7

f3147c，

2.

fX7x2c28,x3,3■-fxmaX

■■gx6x28x

40

23x

10

x2

，agX0在区间3,3上只有一个解X2o

gXming2

48，

a147

c

48，

即c195.

（4）存在X1,X2

3,3

，都有

f

X1g

X2，等价于fminX1gmax他，由⑶得fmin为

f2

c28，

gmaxX2g

3

102，

c28

102c130

点评：

本题的三个小题，表面形式非常相似,

究其本质却大相径庭，应认真审题，深入思考，多加训练，准确使用其成立的充要条件。

解析：

由方程logaXlogay

32

3可得y—，对于任意的x[a,2a]，可得—

x

a2

a3

a2

，依题意得

25

答案：

-

13

99

解析：

由不等式a（xy）

（xy）2可得a

解：

原不等式有解asin2x4sinx1

sinx2

解：

画出两个凼数yax和y,X4X在X

0,3

sinx

y，由线性规划可得1

1有解，而sinx2

3

min

所以

上的图象如图知当x3时y.3，

a上3，x0,3时总有ax

3

6、解：

（I）

2

f（x）x4ax

3a2（1分）

a）和（3a,+

）

令f（X）

0,得f（x）的单调递增区间为（a,3a）

令f（X）

0,得f（x）的单调递减区间为（—

3

•:

当x=a时,

f（x）极小值=a3b;

4

当x=3a时,

f（x）极小值=b.（6分）

（H）由|

f（x）Ka,得一a—x2+4ax—3a2冬a.◎（7

分）

■/02a.二f（x）

x24ax3a2在[a

1,a

2］上是减函数.

（9分）

■-f（x）maxf（a1）

2a1.f（x）min

f（a

2）

4a4.

于是，对任意x［a1,a

2］，不等式①恒成立,

等价于

4,解得4

2a1.5

a1.

7、解:

（1）TOA-[y+2f/

（1）]0B+ln（x+1）OC=0,

/■OA=[y+2f/

（1）]OB-ln（x+1）OC

由于A、B、C三点共线即[y+2f/

（1）]+[-ln（x+1）]=1/■y=f（x）=ln（x+1）+1—2f/

（1）

11

f/（x）=x+1，得f/

（1）=2，故f（x）=ln（x+1）4分

2x12（x+2）—2xx2

（2）令g（x）=f（x）—x+2，由g/（x）=x+1―（x+2）2=（x+1）（x+2）2

Tx>0，■g/（x）>0，■g（x）在（0，+*）上是增函数6分

故g（x）>g（0）=0

2x即f（x）>x+28分

2xx3—x

11

令h（x）=2x2—f（x2）=2x2—ln（1+x2），由h/（x）=x—1+x2=1+x2

10分

当x€［—1，1］时，h（x）max=0,二m2—2bm—3>0

令Q（b）=m2—2bm

Q

（1）=m2—2m—3>0

—3，贝UQ（—1）=m2+2m—3>0得m>3或m

12分

8、解：

（I）

pe

2lne

（II）由

（I）

qe卫2

e

px

2

px

2x

x

2

px

2x

要使fX

在其定义域（0,+）内为单调函数，只需

h（x）在（0,+）内满足：

h（x）>0或h（x）<0恒成

立.

①当p

0时,

2

px

0,

2x0

hx0，所以fx在（0,+）

内为单调递减，故p0；

②当p

0时,

px22x

，其图象为开口向上的抛物线，对称轴为

1

p，只需

p

10，即p>1时,

p

h（x）>0，fx

f（x）

在（0,+

）内为单调递增，故p>1

适合题意.

综上可得,

2e

（III）■■

g（x）=—在［1,e］上是减函数

x=e时，g（x）min=2，x=1时，g（x）max=2e即g（x）

［2,2e］

10分

1

，不合题意。

p<0时，由（II）知f（x）在［1,e］递减f（x）max=f

（1）=0<2

1

20

>0

11

f（x）=p（x—^）—2lnx

f（x）vx—x—2lnxve—e—2lne=e—e—2<2，不合题意。

12分

3p>1时，由（II）知f（x）在［1,e］连续递增，f

（1）=0<2，又g（x）在［1,e］上是减函数

本命题f（x）max>g（x）min=2,x［1,e］

14e

f（x）max=f（e）=p（e—e）—2lne>2p>e2—113分

4e

综上，p的取值范围是（e2—1，+）14分

2）.当a1时f（x）在［-1，2］上是增函数，此时f（-1）=1+2a+4

1

（3）原不等式等价于2x2—f（x2）