MATLAB计算方法与实现.docx
《MATLAB计算方法与实现.docx》由会员分享,可在线阅读,更多相关《MATLAB计算方法与实现.docx(20页珍藏版)》请在冰豆网上搜索。
MATLAB计算方法与实现
(1):
恢复窗口:
在Desktop中下拉式菜单中的DesktopLayout,选择Default来恢复。
(2):
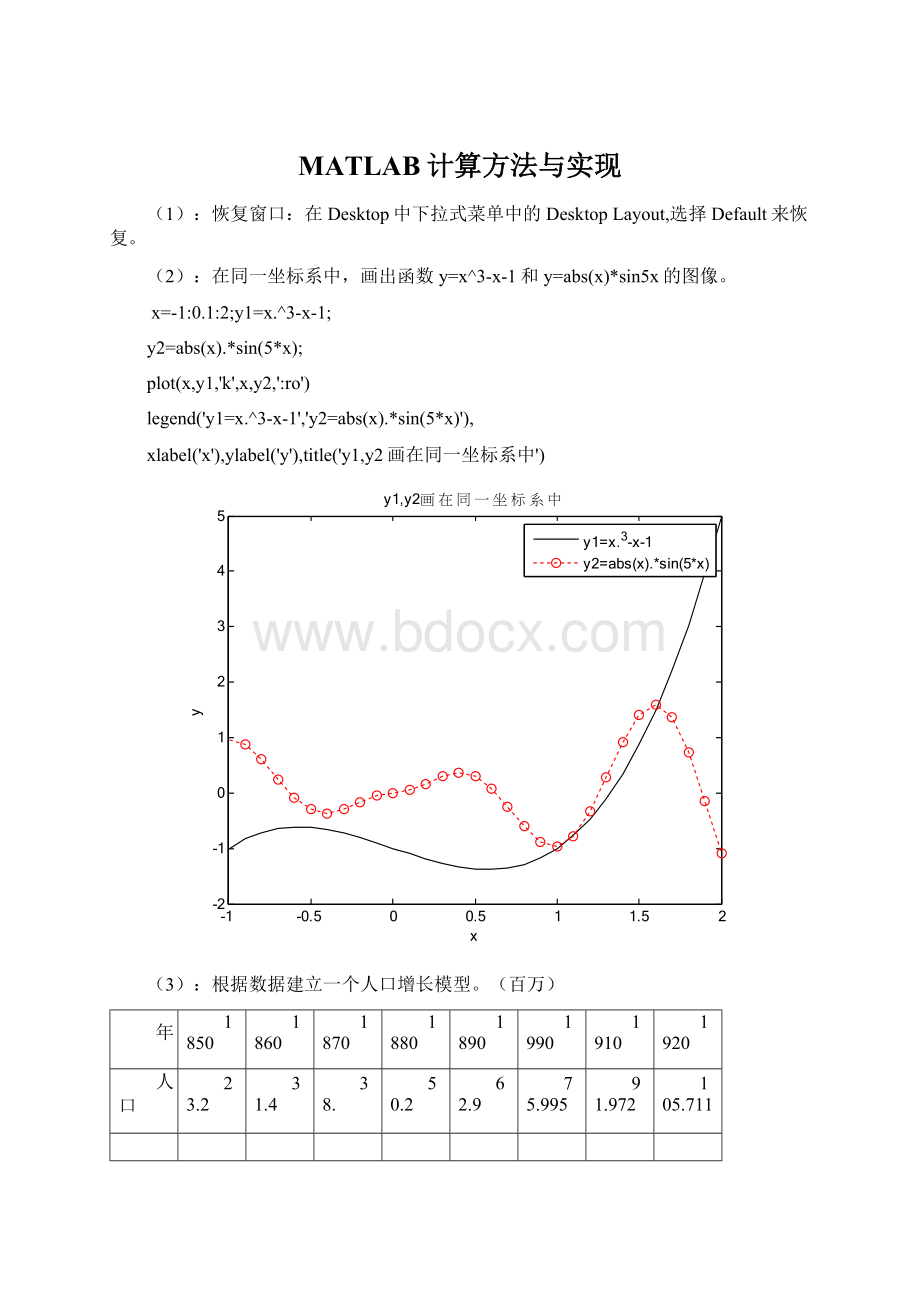
在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x的图像。
x=-1:
0.1:
2;y1=x.^3-x-1;
y2=abs(x).*sin(5*x);
plot(x,y1,'k',x,y2,':
ro')
legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),
xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')
(3):
根据数据建立一个人口增长模型。
(百万)
年
1850
1860
1870
1880
1890
1990
1910
1920
人口
23.2
31.4
38.
50.2
62.9
75.995
91.972
105.711
年
1930
1940
1950
1960
1970
1980
1990
2000
人口
123.203
131.699
150.697
179.329
203.212
226.505
249.633
281.422
解题思路:
首先将表格中的数据转变为MATLAB能处理的矩阵,然后把人口数量看成年份的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Commandwindow中输入:
t=1850:
10:
1990;
p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633];
%读取数据
plot(t,p,’o’);axis([185020200400]);
title(‘PopulationoftheU.s.1850-1990’);
ylabel(‘Millions’);%绘制出数据的函数图形并加以修饰
f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2
v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值
abs(v-251.422)%计算两个模型与2000年人口数的绝对误差。
ans=
28.956130.8937
由计算结果可以确定3阶多项式可作为此问题的数学模型,因此进一步进行预测:
V1=polyval(f1,2010)
V1=
311.6136
即由3阶多项式拟合可预测到2010年美国人口将达到311.6148百万人。
(4):
研究捕食者与被捕食者(Lotka-Voltrra)模型的相互作用系数和的影响。
X’1=x1-x1x2
X’2=x2+x1x2
X1(0)=x2(0)=1,0<=t<=10
建立M文件,再调用微分方程求解器ode45求出数值解。
functiondx=lotka(t,x)
globalalphabeita
dx=[x
(1)-alpha*x
(1)*x
(2);-x
(2)+beita*x
(1)*x
(2)];
第二步:
调用ode45命令求数值解。
在CommandWindow中输入下面的命令。
globalalphabeita
alpha=0.1;beita=0.2;
[t,x]=ode45('lotka',[0,10],[1,1]);%求模型的数值解
plot(t,x(:
1),'k',t,x(:
2),':
k')%画模型的图像解
title('alpha=0.1;beita=0.2,Lotka-Voltrra'),
xlabel('t'),ylabel('x1,x2'),
legend('x1’,'x2'),
第二章
MATLAB的变量是以字母开头,由字母,数字,下划线组成。
同一字母的大小写表示不同的变量。
常见的变量有四种:
数值变量(double)字符变量(char)符号变量(sym)结构变量(struct)。
MATLAB存储变量时用图标和文字来注明变量的类型。
例如输入:
x1=1/3x2=’1/3’x3=sym(‘1/3’)x4.x=1/3
可以在workspace中看到它们各自不同的图标和变量类型的文字解释。
它们分别是double型,char型,sym型,struct型变量。
下面主要讨论数值型变量的有关问题。
在MATLAB中,不用事先定义变量的特性(实数或复数),也不用事先定义变量的维数。
一旦某个变量被赋值,则该变量连同其值将被存放于Workspace中,直到该变量被清除或被重新赋值。
例如在CommandWindow中输入A=5+4i,b=5-4*i,c=8都将是有效的。
如想观察A的值,可在ComamndWindow中输入变量名,然后再按回车键。
如果再输一次A=5,观察A时就不是先前的5+4i了。
在MATLAB中,有些字符被自动赋值,可称之为固有变量。
还有些字符已被MATLAB定义为函数名或M文件名。
因此,在定义变量名时,要尽量回避固有变量名,函数名和M文件名。
下面这些字符是常见的固有变量。
在定义时变量时,一定不要将它们重新赋值。
iorj:
虚数单位,即根下负1
pi:
圆周率
eps:
机器误差:
=2^-52=2.2204*10^-16
realmin:
最小正实数:
2^-1022=2.2251*10^-308
realmax:
最大正实数:
(2-^
Inf:
无穷大
NaN:
非数
ans:
当前答案
(2):
MATLAB默认的数据显示格式是short格式,可以通过键入formatV来改变显示格式。
其中V为所需的显示格式。
MATLAB提供的显示格式有:
short5位固定点格式,如:
3.1416
long15位双精度固定点格式如:
3.14159265358979
shorte5位浮点格式,如:
3.1416e+000
longe15位双精度7位单精度浮点格式,如:
3.141592653589793e+000
shorteng5位工程格式,如:
3.1416e+000
longeng16位工程格式,如:
3.14159265358979e+000
(3):
特殊含义的符号
[]中括号,用于生成矩阵
()圆括号,函数参数的引入符号以及运算次序规则符号
,逗号,在句尾表示换行,并显示结果;在矩阵中则是元素分隔符
;分号,在句尾表示换行,不显示结果;在矩阵中表示换行
‘单引号,是一运算符,表示矩阵转置运算
:
冒号,是一运算符,可生成一等差序列并表示成向量
%百分号,从它起直到它所在的行尾,其间所有的命令,计算机均不执行,即%是一个注释符
@函数句柄
“引号
.点。
小数点。
在算术运算符前表示点对点运算;在变量中加点,表示该变量为结构变量
···续行符
第三章矩阵的操作
3.1
生成矩阵的三种基本方法:
直接输入,由外部文件下载输入,利用MATLAB的函数来生成。
直接输入的两种方法:
方式一:
在CommandWindow中直接输入
例如:
A=[1-10;1/231/3;0101]回车即可
A=
1.0000-1.00000
0.50003.00000.3333
010.00001.0000
方式二:
矩阵编辑器输入。
首先在CommandWindow中输入B=1;接着在Workspace中双击B的图标,调出数组编辑器(ArrayEditor)在表格中输入相应的元素,关闭数组编辑器,则Wordspace中存放的就是所需的矩阵B,以后就可以直接调用。
矩阵也可以由外部数据文件导入。
先将其拷贝下来并粘贴到Excel或记事本中,然后保存为B.csv或B.txt文件。
例如,假设已将B.txt存放于C:
\matlab\work中只需在MATLAB的File菜单下选ImportData,然后选中B并打开,根据提示选Next和Finish.当Workspace中出现了B的标记后。
说明已成功输入了B。
当然还可以通过编写程序来得到某个矩阵。
键入0:
10
ans=
012345678910
键入hilb(3)得到Hilbert矩阵
ans=
1.00000.50000.3333
0.50000.33330.2500
0.33330.25000.2000
键入rand(3,2),可得到3*2的矩阵:
rand(3,2)
ans=
0.95010.4860
0.23110.8913
0.60680.7621
这样的命令很多,可以通过键入命令helpelmat查看。
zeros(m,n)m*n零矩阵
ones(m,n)元素全为1的m*n矩阵
eye(m,n)m*n辨识矩阵,主对角元素全为1,其余元素全为0;若m=n则eye(m)为m阶单位阵
rand(m,n)m*n随机矩阵,其中元素服从离散均匀分布
randn(m,n)m*n随机矩阵,其中元素服从离散正态分布
hadamard(n)n阶Hadamard矩阵
hankel(n)n阶Hankel矩阵
hilb(n)n阶Hilb矩阵
invhilb(n)n阶Hilbert逆矩阵
magic(n)n阶幻方矩阵
pascal(n)n阶pascal矩阵
下面介绍函数命令linspace和运算符号——冒号。
它们都可以用来生成行向量(特殊矩阵)
linspace(x1,x2)以x1为起点,以x2为终点等距生成100个数据的行向量
linspace(x1,x2,N)以x1为起点,以x2为终点等距生成N个数据的行向量
x1:
x2生成以x1为起点,以x2为终点,步长为1的行向量,要求x2>x1
x1:
t:
x2生成以x1为起点,以x2为终点,步长为t的行向量(可以有t<0)
3.2
矩阵结构的变换
diag(v)
若v为矩阵(不一定是方阵),则diag(v)生成以v的主对角元素为元素的列向量。
而daig(v,k)生成以v的第k条对角线元素为元素的列向量。
K=0表示主对角线,k>0表示主对角线的上方,k<0表示主对角线的下方。
若v为n维向量,则diag(v)生成以v为主对角元素的n阶方阵,而diag(v,k)生成n+\k\阶方阵,且v为此方阵的第k条对角线元素。
blkdiag
主对角元素为子矩阵的对角矩阵。
例如输入:
A=[1,2;3,4];B=[5,6];
blkdiag(A,B)
ans=
1200
3400
0056
tril
提取下三角矩阵。
调用规则(A,k)。
其中A为矩阵,k=0表示提取A的主对角线及其下方的元素而成的下三角矩阵,切可缺省;k>0表示提取A的主对角线上方第k条对角线及其下方的元素而成的下三角矩阵;k<0表示提取A的主对角线下方第k条对角线及其下方的元素而成的下三角矩阵。
例如:
A=[1,2,3,4;11,2,5,6;22,33,3,7]
tril(A)
A=
1234
11256
223337
ans=
1000
11200
223330
>>tril(A,2)
ans=
1230
11256
223337
>>tril(A,-2)
ans=
0000
0000
22000
triu
提取上三角矩阵,调用格式triu(A,k),规则与tril的规则相同。
在线性代数中常常会交换矩阵的两行或两列,划去矩阵的某行或某列,提取矩阵的某个子矩阵等这样的一些操作。
实现方法:
设有m*n矩阵A其第i行第j列表示为A(i,j).(矩阵的标识)
从中取出第二行第三列的元素,
A=[1234;5678;9101112];
A(2,3)
ans=
7
把7改为其他元素:
>>A(2,3)=0;
A
A=
1234
5608
9101112
矩阵的标识A(i,j)中,i或j不仅可以是正整数,还可以是冒号或向量。
例如,A(i,:
)
表示A的第i行元素。
而A(i,[2,3])表示A的第i行,第2,3列的元素。
利用矩阵的标识命令可以完成从矩阵A中提取子矩阵,划去矩阵的行或列及交换矩阵的行或列。
A(2,:
)
ans=
5608
>>A([1,2],[2,3])
ans=
23
60
划去A的第2行
>>B=A([1,3],:
)
B=
1234
9101112
第1列和第2列交换,第3列和第4列交换
>>D=A(:
[2143])
D=
2143
6580
1091211
还可以用空矩阵划去某行或某列的操作。
空矩阵的表达式[]键入X=[]
X=
[]
它表示矩阵不含有任何元素,是一个空矩阵。
空矩阵不是0,也不是不存在。
A=(m,:
)=[]表示删除A的第m行元素
A=(:
n)=[]表示删除A的第n列元素
A=[123456;789101112;131415161718];
A(:
[2,5])=[]
A=
1346
791012
13151618
MATLAB可以将若干个子矩阵拼装成一个大矩阵。
a11=[12];a12=3;a13=[456];
a21=[78;1314];a22=[9;15];a23=[101112;161718];
A=[a11a12a13;a21a22a23]
A=
123456
789101112
131415161718
A.*B的运算规则是;矩阵A,B以及运算结果都是同阶矩阵,且A.*B是A,B的对应元素相乘。
已知x=0,1,2,3,4.5,5.5,6.5求y=x^2+3x所对应的值。
x=[0,1,2,3,4.5,5.5,6.5];
y=x.*(x+3)
y=
Columns1through6
04.000010.000018.000033.750046.7500
Column7
61.7500
x=-10:
1:
10;
y=x.*(x+3);
plot(x,y,'k')
x1=0:
3;x2=4.5:
6.5;x=[x1x2];
y=x.*(x+3);
plot(x,y,'k')
>>y
y=
Columns1through6
04.000010.000018.000033.750046.7500
Column7
61.7500
矩阵的除法运算(省略)
MATLAB的命令函数
5.1基本函数
可以在CommandWindow中输入helpelfun命令查到所有的基本函数(标量函数)。
定义域和值域都是复数集。
只有函数realpow(.)和reallog(.)realsqrt()的定义域才与数学中相应函数的定义域相同。
例如:
sqrt
(2)
ans=
1.4142
>>sqrt(i)
ans=
0.7071+0.7071i
>>realsqrt(i)
?
?
?
Errorusing==>realsqrt
Realsqrtproducedcomplexresult.
这些函数的输入参数可以是矩阵。
例如:
x=[12;34];
y=sqrt(x)
y=
1.00001.4142
1.73212.0000
(2)
x=1:
7;
y=sin(x)
y=
0.84150.90930.1411-0.7568-0.9589-0.27940.6570
>>y=x.*sin(x)
y=
0.84151.81860.4234-3.0272-4.7946-1.67654.5989
5.2
数据分析函数(DataAnalysis)
在ComamandWindow中输入helpdatafun查到所有的数据分析函数。
一般来说,数据分析函数的输入量应是列向量(数据分析函数又被称为向量函数)。
如果是行向量,数据分析函数同样可以计算。
如果输入矩阵,则数据分析函数按列向量计算。
max([1432])输入的是行向量
ans=
4
x=
169
243
3210
>>x=[169;243;3210];
max(x)
ans=
3610(按列向量)
5.3矩阵函数(MatrixFunctions)
所谓矩阵函数是指函数命令的输入变量为矩阵。
可以在CommandWindow窗口中键入helpmatfun命令查到所有的矩阵函数。
用help+函数名的方法,可以对其中任一函数的功能作进一步的了解。
关于矩阵分析的命令:
norm(X)求矩阵或向量的范数,对于矩阵X而言是X的最大奇异值,也就是X的2范数
norm(X,2)与norm(X)相同
norm(X,1)X的1范数
norm(X,inf)X的无穷范数
rank(A)求矩阵A的秩
det(A)求方阵A的行列式
trace(A)矩阵A主对角元素之和
rref(A)对矩阵A进行初等变换,变换成阶梯型矩阵
A=[1234;5101520;6789];
rref(A)
ans=
10-1-2
0123
0000
2;关于解线性方程组的命令(LinearEquations)
/和\线性方程组的求解命令
inv(A)求方阵A的逆
cond(A)求A的条件数
chol(A)求正订方阵A的Cholesky分解
lu(A)求A的LU分解,调用格式一般为[L,U]=lu(X),其中U是上三角矩阵,L是一个下三角矩阵且满足X=L*U,允许X不是方阵。
pinv(A)求矩阵A的伪逆
a=[1023;234;348];
chol(a)
ans=
3.16230.63250.9487
01.61252.1086
001.6291
A=[10-70;-326;5-15];
[L,U]=lu(A)
L=
1.000000
-0.3000-0.04001.0000
0.50001.00000
U=
10.0000-7.00000
02.50005.0000
006.2000
5.3求特征值和奇异数的命令
eig(A)求A的特征值和特征向量。
调用格式一般为E=eig(A)或[V,D]=eig(A).E是方阵A的特征值构成的向量,D是以A的特征值为主对角线元素的对角矩阵,V是与特征值相对应的特征向量所构成的满秩矩阵,且满足A*V=V*D
svd(A)求A的奇异值分解,调用格式一般为:
[U,S,V]=svd(X),其中S是一个维数与X相同的对角矩阵,且对角线元素非负递减,U和V是酒矩阵,且满足X=U*S*V’
ploy(A)
求矩阵的特征多项式和以1,-1,0为根的多项式。
e=poly([01;02])
e=
该矩阵的多项式为e=x^-2x
1-20
>>c=poly([1-10])
c=
10-10
多项式为c=x^3-x
6.1平面曲线的绘制
在x-y坐标面上绘制函数图形的主要命令是plot。
其调用格式是plot(x,y),其中x是向量,y是与x同维的向量。
x=-pi:
0.01:
pi;
y=x.*sin(x);
plot(x,y)
Plot的调用格式还可以是plot(x1,y1,x2,y2,x3,y3``````),用于同一坐标系下绘制多条函数曲线。
其中一组(xi,yi)表示一组函数。
x1=-3:
0.05:
3;x2=-2.9:
0.02:
2.9;
y1=sin(x1.^2);y2=exp(-x2.^2);
plot(x1,y1,x2,y2)
1:
曲线的修饰
设S使修饰变量,用plot(x,y,s)或plot(x1,y1,S1,x2,y2,s2…….)可以对曲线y的线型和颜色进行修饰。
S是一个单引号括起来的字符。
字符可以是下表的任意一种颜色和(多个)线型字符的组合。
字符
b
g
r
c
m
y
k
色彩
蓝
绿
红
青
洋红
黄
黑
字符
.
o
x
+
*
s
d
v
线型
点
圆
叉
加号
星号
正方形
宝石型
上三角
字符
^
<
>
p
h
--
:
-.
线型
下三角
左三角
右三角
五角星
六角星
长虚线
虚线
点线
还可以用plot(x,y,S,’LineWidth’,a)来绘制曲线函数,a(曲线宽度)可取(0.5,1,2,3,4,6,8,10,15,25,30)
2:
坐标轴的控制
命令axis被用来控制坐标轴的范围。
常用格式为:
axis([xminxmax,ymin,ymax])指定x,y的取值范围
axisequal使x,y轴的单位长度相等
axisaquare使坐标面为正方形
3:
图形标注,说明,网格
(1):
图形标注命令
title(‘S’)题头标注,S为说明文的字符
xlabel(‘S’)X轴标注,S为说明文的字符
ylabel(‘S’)Y轴标注,S为说明文的字符
3:
图形说明命令
legend(‘S1’,’S2’,’Sn’,pos)线性说明,Si为说明文字符。
Pos为整数,用来指定标注的位置
pos=-1坐标系范围外右边
pos=0坐标系范围内,并尽可能少的遮挡曲线
pos=1坐标系范围内右上角,是默认值
pos=2坐标系范围内左上角
pos=3坐标系范围内左下角
pos=4坐标系范围内右下角
(3)网格命令
gridon在坐标面上画网格
gridoff在坐标面上去除网格
grid在两者之间切换
x1=-3:
0.05:
3;x2=-2.9:
0.02:
2.9;
y1=sin(x1.^2);y2=exp(-x2.^2);
plot(x1,y1,x2,y2)
x=-pi:
0.01:
pi;
x=-pi:
0.01:
pi;
x=-pi:
0.01:
pi;
y1=sin(x);y2=cos(x);y3=sin(x)-cos(x);
plot(x,y1,'r',x,y2,'k',x,y3,'g','linewidth',2)
axisequal
grid
legend('