圆锥曲线综合讲义及答案.docx

圆锥曲线综合讲义及答案.docx

《圆锥曲线综合讲义及答案.docx》由会员分享，可在线阅读，更多相关《圆锥曲线综合讲义及答案.docx（12页珍藏版）》请在冰豆网上搜索。

圆锥曲线综合讲义及答案

知识点睛

圆锥曲线综合（讲义）

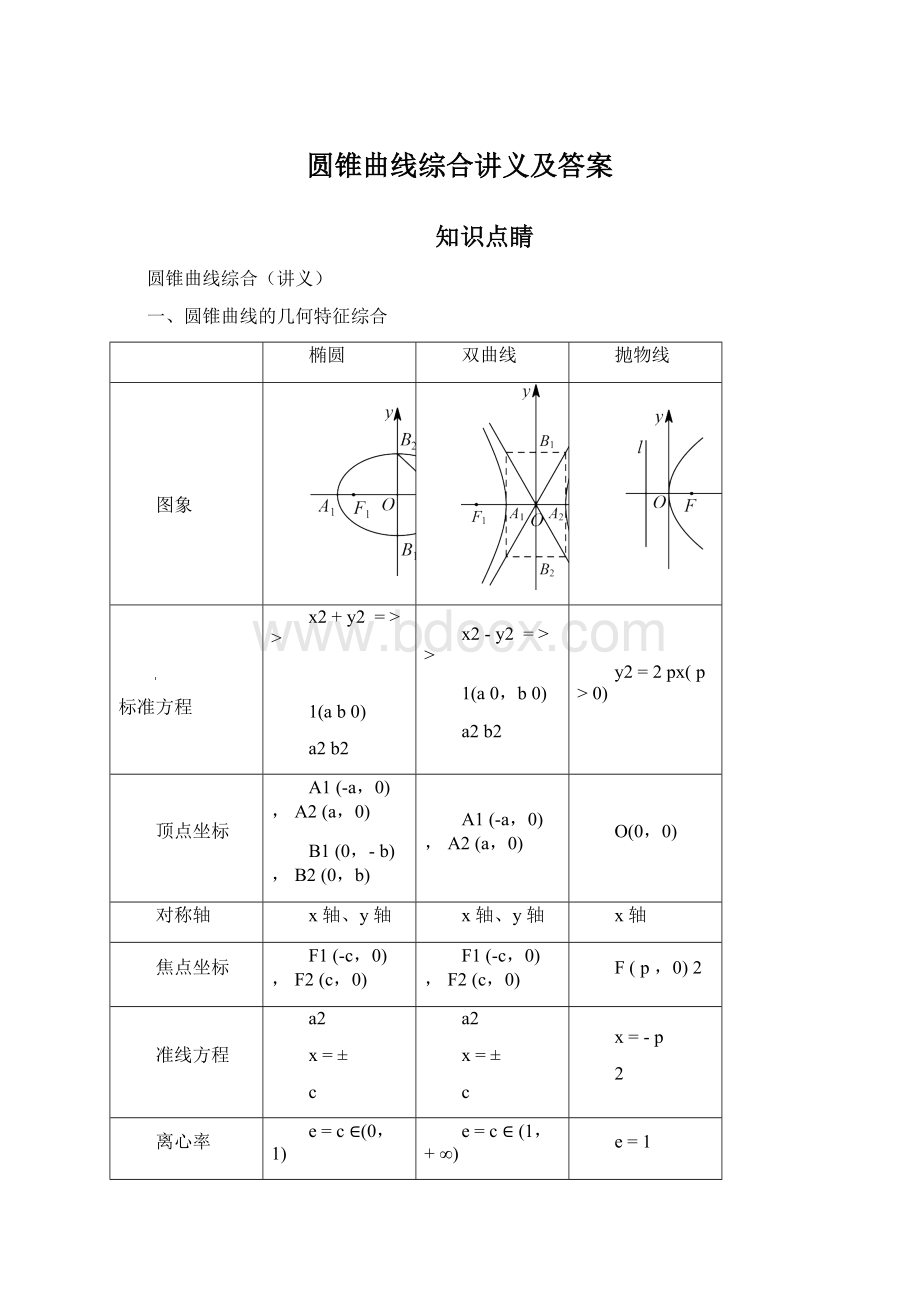
一、圆锥曲线的几何特征综合

椭圆

双曲线

抛物线

图象

标准方程

x2+y2=>>

1（ab0）

a2b2

x2-y2=>>

1（a0，b0）

a2b2

y2=2px（p>0）

顶点坐标

A1（-a，0），A2（a，0）

B1（0，-b），B2（0，b）

A1（-a，0），A2（a，0）

O（0，0）

对称轴

x轴、y轴

x轴、y轴

x轴

焦点坐标

F1（-c，0），F2（c，0）

F1（-c，0），F2（c，0）

F（p，0）2

准线方程

a2

x=±

c

a2

x=±

c

x=-p

2

离心率

e=c∈（0，1）

a

e=c∈（1，+∞）

a

e=1

a，b，c的

关系

c2=

c2=

无

注：

只讨论了其中一种情况

1

二、圆锥曲线与直线的位置关系

1.圆锥曲线与直线的交点的个数问题

把圆锥曲线方程与直线方程联立消去y（或x），整理得到关于x（或y）的方程ax2+bx+c=0（或ay2+by+c=0），判断方程的解的个数．

2.圆锥曲线与直线的相交弦长问题

设斜率为k（k≠0）的直线l与圆锥曲线C相交于A，B两点，

A（x1，y1），B（x2，y2），则

|AB|=

=|x-x|=

|y-y|

1212

3.弦的中点问题点差法

在求解圆锥曲线并且题目中交代直线与圆锥曲线相交和被截的线段的中点坐标时，设出直线与圆锥曲线的两个交点坐标，代入圆锥曲线的方程并作差，从而求出直线的斜率，然后利用中点坐标求出直线方程．

2

精讲精练

1.实数变量m，n满足m2+n2=1，则坐标（m+n，mn）表示的点

的轨迹是（

）

A．椭圆

C．抛物线

B．双曲线的一支

D．抛物线的一部分

2.已知抛物线y2

=4x的准线与双曲线

x2

-2

a2y

=1（a>0）相交于

A，B两点，且F是抛物线的焦点，若△FAB是直角三角形，则双曲线的离心率为（）

A.

B．

C．2D．3

3

3.已知M是y=1x2上一点，F为抛物线的焦点．若点A在圆

4

C：

（x-1）2+（y-4）2=1上，则|MA|+|MF|的最小值为（）

A．2B．4C．8D．10

4.

已知抛物线y2=2px（p>0）上一点M（1，m）（m>0）到其焦点

的距离为5，双曲线

x2

-2

a2y

=1（a>0）的左顶点为A，若双曲线

的一条渐近线与直线AM平行，则实数a的值是（）

A.1

9

B.

1

25

C.

1

5

4

D.

1

3

5.已知A（0，7），B（0，-7），C（12，2），以C为一个焦点的椭圆经过A，B两点，则椭圆的另一个焦点F的轨迹方程是（）

A.y2

x2

1（y≤1）

48

B.

y2

x2

1（y≥1）

48

C.x2

y2

1（x≤1）

48

D.

x2

y2

1（x≥1）

48

6.

设点A为圆（x-1）2+y2=1上的动点，PA是圆的切线，且

|PA|=1，则P点的轨迹方程为（）

A．y2=2x

C．y2=-2x

B．（x-1）2+y2=4

D．（x-1）2+y2=2

5

7.已知抛物线y2=8x的焦点为F，直线y=k（x-2）与此抛物线

相交于P，Q两点，则1+1

=（）

A．1

2

8.

2

已知椭圆C：

x

a2

|FP||FQ|

B．1C．2D．4

+=>>

y2

1（ab0）的左焦点为F，椭圆C与过

b2

原点的直线相交于A，B两点，连接AF，BF．若|AB|=10，

|AF|=6，cos∠ABF=4，则C的离心率e=．

5

6

x2y2

2222

9.点P是双曲线C：

-

ab2

=1（a>0，b>0）与圆x+y=a+b

的一个交点，且2∠PF2F1=∠PF1F2，其中F1，F2分别是双曲线C1的左、右焦点，则双曲线C1的离心率为．

2

2

10.

椭圆x+y=1的左焦点为F，直线x=m与椭圆相交于点A，

43

B．当△FAB的周长最大时，△FAB的面积是．

11.椭圆

x2+2

2

=1的一条弦被点（

11）平分，则这条弦所在的

22

直线方程是．

7

12.如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的

投影，M为PD上一点，且|MD|=4|PD|．

5

（1）当P在圆上运动时，求点M的轨迹C的方程；

（2）求过点（3，0）且斜率为4的直线被C所截线段的长度．

5

8

x2

2

13.已知椭圆C1：

+y

4

相同的离心率．

=1，椭圆C2以C1的长轴为短轴，且与C1有

（1）求椭圆C2的方程；

（2）设O为坐标原点，点A，B分别在椭圆C1，C2上，

−→−→

若OB=2OA，求直线AB的方程．

9

14.

如图，双曲线x

a2

y2

b21（a0，b0）的一条渐近线方程是

y=3x，坐标原点到直线AB的距离为3，其中A（a，0），

2

B（0，-b）．

（1）求双曲线的方程；

（2）若B1是双曲线虚轴在y轴正半轴上的端点，过点B作直线交双曲线于点M，N，求B1M⊥B1N时，直线MN的方程．

回顾与思考

10

7

9．3+110．311．y=-1x+3

24

12．

（1）x+=1；

（2）41

25165

13．

（1）x

2

+=1；

（2）y=±x

416

2

14．

（1）x

2

y

-=1；

（2）y=±

5x-3

39

11