实证研究论文数据分析方法详解.docx
《实证研究论文数据分析方法详解.docx》由会员分享,可在线阅读,更多相关《实证研究论文数据分析方法详解.docx(35页珍藏版)》请在冰豆网上搜索。
实证研究论文数据分析方法详解
修订日:
2010.12.8
实证论文数据分析方法详解
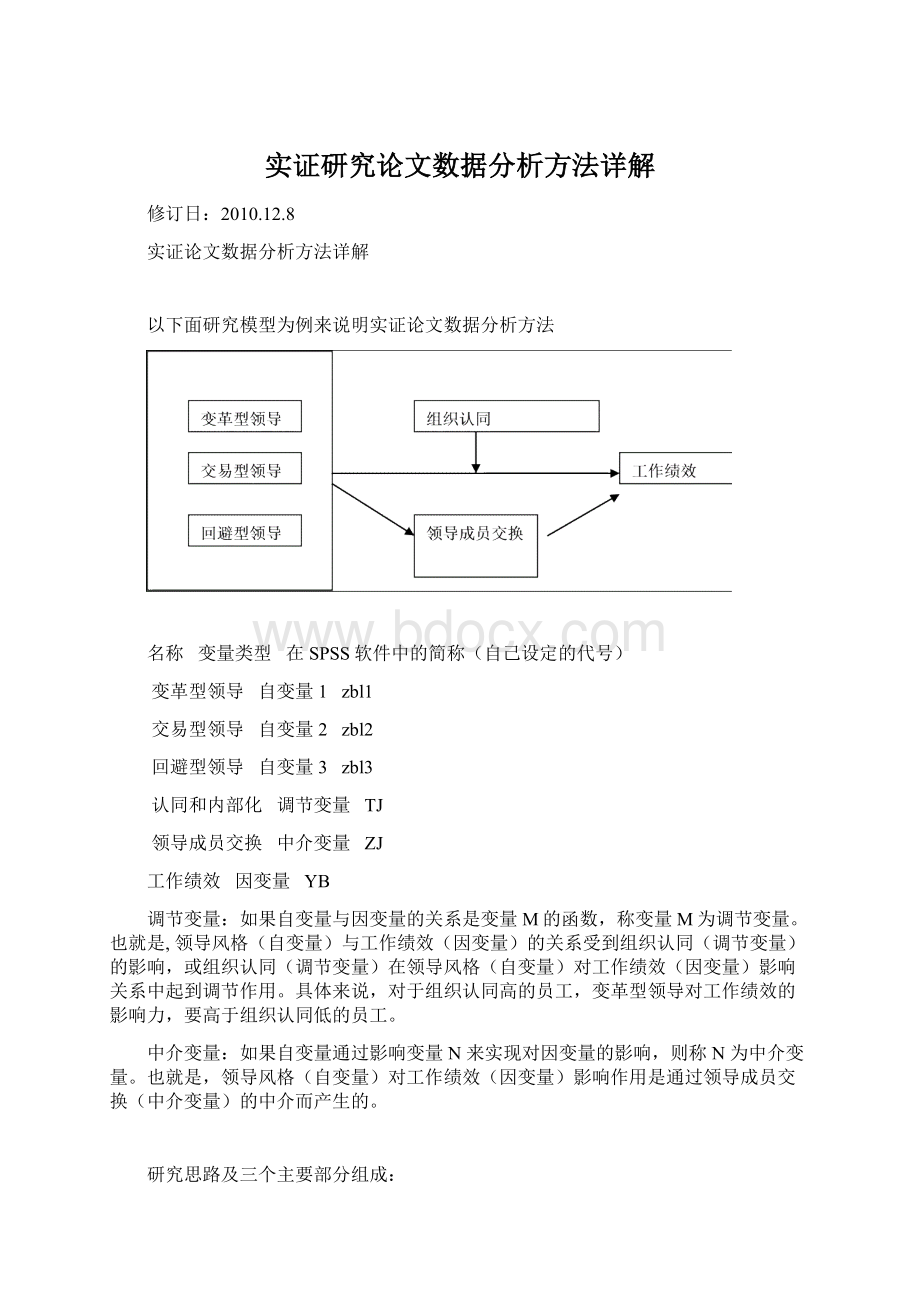
以下面研究模型为例来说明实证论文数据分析方法
名称变量类型在SPSS软件中的简称(自己设定的代号)
变革型领导自变量1zbl1
交易型领导自变量2zbl2
回避型领导自变量3zbl3
认同和内部化调节变量TJ
领导成员交换中介变量ZJ
工作绩效因变量YB
调节变量:
如果自变量与因变量的关系是变量M的函数,称变量M为调节变量。
也就是,领导风格(自变量)与工作绩效(因变量)的关系受到组织认同(调节变量)的影响,或组织认同(调节变量)在领导风格(自变量)对工作绩效(因变量)影响关系中起到调节作用。
具体来说,对于组织认同高的员工,变革型领导对工作绩效的影响力,要高于组织认同低的员工。
中介变量:
如果自变量通过影响变量N来实现对因变量的影响,则称N为中介变量。
也就是,领导风格(自变量)对工作绩效(因变量)影响作用是通过领导成员交换(中介变量)的中介而产生的。
研究思路及三个主要部分组成:
(1)领导风格对于员工工作绩效的主效应(MainEffects)研究。
(2)组织认同对于不同领导风格与员工工作绩效之间关系的调节效应(ModeratingEffects)研究。
(3)领导成员交换对于不同领导风格与员工工作绩效之间关系的中介效应(MediatorEffects)研究。
目录
1.《调查问卷表》中数据预先处理~~~~~~~~~~~~~~3
1.1剔除无效问卷~~~~~~~~~~~~~~~~~~~~3
1.2重新定义控制变量~~~~~~~~~~~~~~~~~~3
2.把Excel数据导入到SPSS软件中的方法~~~~~~~~~~4
3.确认所有的变量中有无“反向计分”项~~~~~~~~~~~4
3.1无“反向计分”题~~~~~~~~~~~~~~~~~~5
3.2有“反向计分”题~~~~~~~~~~~~~~~~~~5
4.效度分析~~~~~~~~~~~~~~~~~~~~~~~~6
5.信度分析~~~~~~~~~~~~~~~~~~~~~~~~8
6.描述统计~~~~~~~~~~~~~~~~~~~~~~~~9
7.各变量相关系数~~~~~~~~~~~~~~~~~~~~12
7.1求均值~~~~~~~~~~~~~~~~~~~~~~~12
7.2相关性~~~~~~~~~~~~~~~~~~~~~~~12
8.回归分析~~~~~~~~~~~~~~~~~~~~~~~13
8.1使用各均值来分别求Z值~~~~~~~~~~~~~~~13
8.2自变量Z值与调节变量Z值的乘积~~~~~~~~~~~13
8.3进行回归运算~~~~~~~~~~~~~~~~~~~~14
8.3.1调节作用分析~~~~~~~~~~~~~~~~~~14
8.3.2中介作用分析~~~~~~~~~~~~~~~~~~18
8.4调节作用作图~~~~~~~~~~~~~~~~~~~~22
1.《调查问卷表》中数据预先处理
1.1剔除无效问卷
《调查问卷表》中有内容对立的题项,主要是测试答题人是否认真阅读和填写本调查问卷表而设置的,例如:
2.2题我在决策过程当中经常发表了自己的意见。
2.8题在决策中我没有发表意见的机会。
可供的回答选项如下:
完全不符合
比较不符合
有点符合
比较符合
完全符合
如果答题者2.2题的回答选,做2.8题的回答却选,则这份调查问卷为无效。
该调查问卷所有数据应事先删除,即:
这份调查问卷不能用做数据分析。
有效的回答为:
如果2.2题的回答选,做2.8题的回答选;或者,如果2.2题选,那么2.8题选。
……等等(依此类推,在此不全部列出)
1.2重新定义控制变量
输入在Excel中的《调查问卷表》数据项,例如:
最高学历、性别、年龄,当前工作时间,等等,诸如此类的描述统计的项目,被统称为“控制变量”
数据导入SPSS之前,在Excel中要事先对“最高学历”、“性别”、“年龄”、“当前工作时间”……等控制变量进行了归类和重新定义,例如:
性别的重新定义:
男性表示为1
女性表示为2
年龄的重新定义:
25岁以下表示为1
25~30岁表示为2
30~35岁表示为3
35~40岁表示为4
40岁以上表示为5
当前工作时间的重新定义:
1年以下表示为1
1~3年表示为2
3~5年表示为3
5~8年表示为4
8年以上表示为5
……等等(依此类推,对其他控制变量进行适当的定义)
2.把Excel数据导入到SPSS软件中的方法
操作方法:
打开SPSS程序,点击在左上角的File——Open——Date——对话框中的“文件类型”项中选择“Excel格式”——选择你要导入的Excel数据文件——点击“打开”——在对话框中的“Range”项定义提取Excel表中数据的范围“最左上角:
最右下角”,例如“B2:
HW217”——数据自动导入到SPSS表格中,在DateView页面中确认一下数据是否少读或多读不需要的信息。
(注意:
在对话框选项“Readvariablenamesformthefirstrowofdate”上打勾或不打勾,对定义Excel表中数据的范围有影响,所以要确认一下数据是否少读或多读不需要的信息)
从“DateView”页面转到“VariableView”页面,根据最左边的“Name”对应“调查问卷”中的问题项,在“Label”列中标明自变量1、自变量2、自变量3、调节变量、中介变量、因变量。
Q1:
在“Label”列中标注什么代号?
A1:
根据个人的喜欢和方便识别、记忆可自己定义,本文的标注是:
自变量1zbl1
自变量2zbl2
自变量3zbl3
调节变量TJ
中介变量ZJ
因变量YB
Q2:
怎样知道哪几行是自变量1、哪几行是自变量2、……、哪几行是因变量?
A2:
导师会事先告诉你,在《调查问卷表》中哪些问题项是属于自变量1、哪些问题项是属于自变量2、……、哪些问题项是属于因变量。
对照《调查问卷表》中各问题项的排列顺序找到SPSS中相应的“行”并作上述标注。
注意:
数据较多,不要看错行,这样会导致运算了其他不相关的数据而造成错误!
3.确认所有的变量中有无“反向计分”项
在做效度分析之前,先要看清楚《调查问卷表》中被选中作为变量的问卷题目有没有要“反向计分”的?
每个变量所对应的问卷题目内容再仔细地一题一题确认一遍。
所谓“反向计分”题是指在同一变量中与其他题目逻辑相反的题。
例如:
5.1题我清楚我的上司对我的满意程度如何。
5.2题我的上司对我的问题和需求了如指掌。
5.3题我的上司没有意识到我的潜力。
←假如这3道题都属于同一变量,第5.3题与其它题的逻辑相反,第5.3题就是“反向计分题”。
在做数据分析时,该题的计分应与其它题相反,因此事先要对该题的计分进行转换,转换方法如下3.2说明
3.1如果没有反向计分题,那么就跳过3.2的步骤,直接进行信度分析、效度分析等
3.2如果有反向计分题,那么执行以下步骤,经过计分转换后,该题才能和其它题一同进行之后的各项数据分析
操作方法:
Transform——Recode——IntoDifferentVariables——在左边的框中找到“反向计分”的项并点击放入到“NumericVariable→OutputVariable”框内——在右边Name框中输入新的名字,比如:
zbl2fanxiang(代表:
自变量2的反向计分项)——点击“OldandNewValues”后进入另一个对话框,如果你的《调查问卷表》中该题是1~5计分范围,那么按以下方法输入:
在OldValue框中键入1后,在NewValue框中键入5,点击Add按钮;
在OldValue框中键入2后,在NewValue框中键入4,点击Add按钮;
在OldValue框中键入4后,在NewValue框中键入2,点击Add按钮;
在OldValue框中键入5后,在NewValue框中键入1,点击Add按钮;
最后,按Continue按钮,完成计分转换的设定,再按OK键完成。
生成新的1行,即:
自变量2反向计分项(代号:
zbl2fanxiang),出现在“VariableView”页面所有数据行的最下面1行。
不要遗忘的注意点:
在此后的运算(效度分析,信度分析,求均值),凡是涉及到要使用该项时,均用新生成的自变量2反向计分项(代号:
zbl2fanxiang)代替原有项进行运算。
4.效度分析
操作方法:
Analyze——DateReduction——FactorAnalysis——在左边的框中把所有自变量1的项(标注为:
zbl1)全都放到Variables框中去,点击OK,完成自变量1的效度分析。
重复以上操作,自变量2、自变量3、调节变量、中介变量、因变量都要分别做效度分析。
结果如下:
(只要Copy出必要的数据即可,不用把生成的所有结果都Copy出来)
判断标准:
看下表Component的值,如果全部都在0.5以上就有效,0.7以上载荷就好;
如果出现载荷小于0.5的变量题项,那么就筛除该题项。
筛除方法:
记住该变量的题项在下表ComponentMatrix(a)的位置顺序,并在SPSS软件的“VariableView”页面中找到相对应的数据行,在“Label”格中删除先前标注的变量代号,总而言之,就是今后在做任何运算时都不要用到该项。
结果如下:
“
bl1:
(自变量1)变革型领导
ComponentMatrix(a)
Component
1
zbl1
.732
zbl1
.763
zbl1
.740
zbl1
.790
zbl1
.786
zbl1
.803
zbl1
.777
zbl1
.711
zbl1
.778
zbl1
.788
zbl1
.789
zbl1
.770
zbl1
.768
zbl1
.770
zbl1
.816
zbl1
.784
zbl1
.762
zbl1
.760
ExtractionMethod:
PrincipalComponentAnalysis.
a1componentsextracted.
bl2:
(自变量2)交易型领导
ComponentMatrix(a)
Component
1
zbl2
.809
zbl2
.803
zbl2
.792
zbl2
.810
ExtractionMethod:
PrincipalComponentAnalysis.
a1componentsextracted.
bl3:
(自变量3)回避型领导
ComponentMatrix(a)
Component
1
Zbl3
.839
Zbl3
.897
Zbl3
.713
Zbl3
.884
Zbl3
.796
Zbl3
.819
Zbl3
.821
Zbl3
.514
……等等(此处省略,不一一列出各表格)
根据以上这些结果作出下面这样的表格放在论文中即可(在论文中表格要居中放置)如下:
变革型领导的因子载荷矩阵
Component
1
变革型领导
.732
变革型领导
.763
变革型领导
.740
变革型领导
.790
变革型领导
.786
变革型领导
.803
变革型领导
.777
变革型领导
.711
变革型领导
.778
变革型领导
.788
变革型领导
.789
变革型领导
.770
变革型领导
.768
变革型领导
.770
变革型领导
.816
变革型领导
.784
变革型领导
.762
变革型领导
.760
……等等(依此类推,作出各变量表格放在论文中)
5.信度分析
操作方法:
Analyze——Scale——ReliabilityAnalysis——在左边的框中把所有自变量1的项(标注为:
zbl1)全都放到Variables框中去,点击OK,完成自变量1的信度分析。
重复以上操作,自变量2、自变量3、调节变量、中介变量、因变量都要分别做信度分析。
结果如下:
(只要Copy出必要的数据即可,不用把生成的所有结果都Copy出来)
判断标准:
看下表Cronbach'sAlpha的值,如果全部都在0.7信度以上就可以接受;
如果信度小于0.7,那么就要检查是否存在反向计分的题项,或者有些题项信度太低影响总的信度水平,排除这个题项后再算信度看看是否改善。
如果发现这类情况,那么今后在做任何运算时都不要用到该题项。
zbl1:
(自变量1)变革型领导
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.960
18
zbl2:
(自变量2)交易型领导
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.816
4
zbl3:
(自变量3)回避型领导
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.870
8
TJ:
(调节变量)认同和内部化
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.864
3
ZJ:
(中介变量)领导成员交换
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.902
6
YB:
(因变量)工作绩效
ReliabilityStatistics
Cronbach'sAlpha
NofItems
.873
4
根据以上这些结果作出下面这样的表格放在论文中即可(在论文中表格要居中放置)如下:
分量表信度分析汇总表
变量类别
分量表
Cronbach'sAlpha值
自变量
变革型领导
.960
交易型领导
.816
回避型领导
.870
薪酬
0.851
调节变量
组织认同
.864
中介变量
领导成员交换
.902
因变量
员工工作绩效
.873
6.描述统计
描述统计的对象:
本文的《调查问卷表》中:
最高学历、性别、年龄,当前工作时间,等等为描述统计的对象(一般统计员工的数据,有必要时才统计领导数据)。
这些对象被统称为“控制变量”(事先要在数据导入SPSS前,在EXCEL表中先进行归类和重新定义,具体参见第3页1.2章节内容)
操作方法:
Analyze——DescriptiveStatistics——Frequencies——在左边的框中把所有控制变量(如:
最高学历、性别、年龄,当前工作时间、等等)全都放到Variables框中去,点击OK,完成描述统计。
Q1:
“在左边的框中”怎样知道哪个是最高学历、哪个是性别,哪个是年龄……等等的代号?
A1:
对照《调查问卷表》中各问题项的排列顺序找到SPSS中相应的“行标”。
结果如下:
(只要Copy出必要的数据即可,不用把生成的所有结果都Copy出来)
年龄
Frequency
Percent
ValidPercent
CumulativePercent
Valid
1
24
11.2
11.2
11.2
2
45
20.9
20.9
32.1
3
57
26.5
26.5
58.6
4
55
25.6
25.6
84.2
5
34
15.8
15.8
100.0
Total
215
100.0
100.0
25岁以下表示为1
25~30岁表示为2
30~35岁表示为3
35~40岁表示为4
40岁以上表示为5
当前工作时间
Frequency
Percent
ValidPercent
CumulativePercent
Valid
1
26
12.1
12.1
12.1
2
46
21.4
21.4
33.5
3
48
22.3
22.3
55.8
4
46
21.4
21.4
77.2
5
49
22.8
22.8
100.0
Total
215
100.0
100.0
1年以下表示为1
1~3年表示为2
3~5年表示为3
5~8年表示为4
8年以上表示为5
……等等(此处省略,不一一列出各表格)
然后根据这些结果作出下面这样的表格放在论文中即可(在论文中表格要居中放置)如下:
注意:
下表只是为了说明表格的制作式样和方法,所以复制了与本文有些不相关的内容和数据。
被试的组织特征
被试的员工特征
项目
类别
人数(个)
百分比(%)
有效百分比(%)
累计百分比(%)
最高学历
初中
45
20.9
20.9
20.9
高中中专
48
22.3
22.3
43.3
大专
47
21.9
21.9
65.1
本科
57
26.5
26.5
91.6
硕士
18
8.4
8.4
100.0
Total
215
100.0
100.0
性别
男
123
57.2
57.2
57.2
女
92
42.8
42.8
100.0
Total
215
100.0
100.0
年龄
25岁以下
24
11.2
11.2
11.2
25~30岁
45
20.9
20.9
32.1
30~35岁
57
26.5
26.5
58.6
35~40岁
55
25.6
25.6
84.2
40岁以上
34
15.8
15.8
100.0
Total
215
100.0
100.0
当前工作时间
1年以下
26
12.1
12.1
12.1
1~3年
46
21.4
21.4
33.5
3~5年
48
22.3
22.3
55.8
5~8年
46
21.4
21.4
77.2
8年以上
49
22.8
22.8
100.0
Total
215
100.0
100.0
7.各变量相关系数
7.1以下变量分别求均值
自变量1生成新的1行zbl1junzhi
自变量2生成新的1行zbl2junzhi
自变量3生成新的1行zbl3junzhi
调节变量生成新的1行TJjunzhi
中介变量生成新的1行ZJjunzhi
因变量生成新的1行YBjunzhi
操作方法:
Transform——ComputeVariable——TargetVariable框中键入名称(自己定),我这里是键入了zbl1junzhi——在Functiongroup框中选Statistical后,在下方的表中选定Mean并双击,此时在NumericExpression框中出现了“MEAN(?
,?
)”——放入所有属于自变量1(zbl1)的各项到MEAN(zbl1,zbl1,zbl1,…)各项之间用逗号分开——点击OK键——生成新的1行,即:
自变量1均值(代号:
zbl1junzhi),出现在“VariableView”页面所有数据行的最下面1行。
重复以上操作,分别生成各自新的1行即:
自变量2均值(代号:
zbl2junzhi)、自变量3(代号:
zbl2junzhi)、……、因变量均值(代号:
YBjunzhi)。
7.2做相关性
操作方法:
Analyze——Correlate——Bivariate——把自变量1的均值(zbl1junzhi)、自变量2的均值(zbl2junzhi)、自变量3的均值(zbl3junzhi)、调节变量的均值(TJjunzhi)、中介变量的均值(ZJjunzhi)、因变量的均值(YBjunzhi)都放入“Variables”框中——点击OK
结果如下:
Correlations
bl1junzhi
bl2junzhi
bl3junzhi
TJjunzhi
ZJjunzhi
YBjunzhi
zbl1junzhi
PearsonCorrelation
1
.891(**)
-.891(**)
.758(**)
.897(**)
.865(**)
Sig.(2-tailed)
.000
.000
.000
.000
.000
N
215
215
215
215
215
215
zbl2junzhi
PearsonCorrelation
.891(**)
1
-.789(**)
.695(**)
.829(**)
.804(**)
Sig.(2-tailed)
.000
.000
.000
.000
.000
N
215
215
215
215
215
215
zbl3junzhi
PearsonCorrelation
-.891(**)
-.789(**)
1
-.691(**)
-.815(**)
-.797(**)
Sig.(2-tailed)
.000
.000
.000
.000
.000
N
215
215
215
215
215
215
TJjunzhi
PearsonCorrelation
.758(**)
.695(**)
-.691(**)
1
.745(**)
.726(**)
Sig.(2-tailed)
.000
.000
.000
.000
.000
N
215
215
215
215
215
215
ZJjunzhi
PearsonCorrelation
.897(**)
.829(**)
-.815(**)
.745(**)
1
.837(**)
Sig.(2-tailed)
.000
.000
.000
.000
.000
N
215
215
215
215
215
215
YBjunzhi
PearsonCorrelation
.865(**)
.804(**