0517鸡爪定理之六.docx
《0517鸡爪定理之六.docx》由会员分享,可在线阅读,更多相关《0517鸡爪定理之六.docx(7页珍藏版)》请在冰豆网上搜索。
0517鸡爪定理之六
鸡爪定理之六
原创:
西安交大附中金磊金磊讲几何构型金磊讲几何构型
微信号jinleijihe
功能介绍西安交大附中竞赛教练金磊老师个人账号,着重讲解平面几何常见构型(结构模型)及其性质、揭示题目间本质联系、介绍本人的解题思考过程及常用解题方法。
2018-05-17
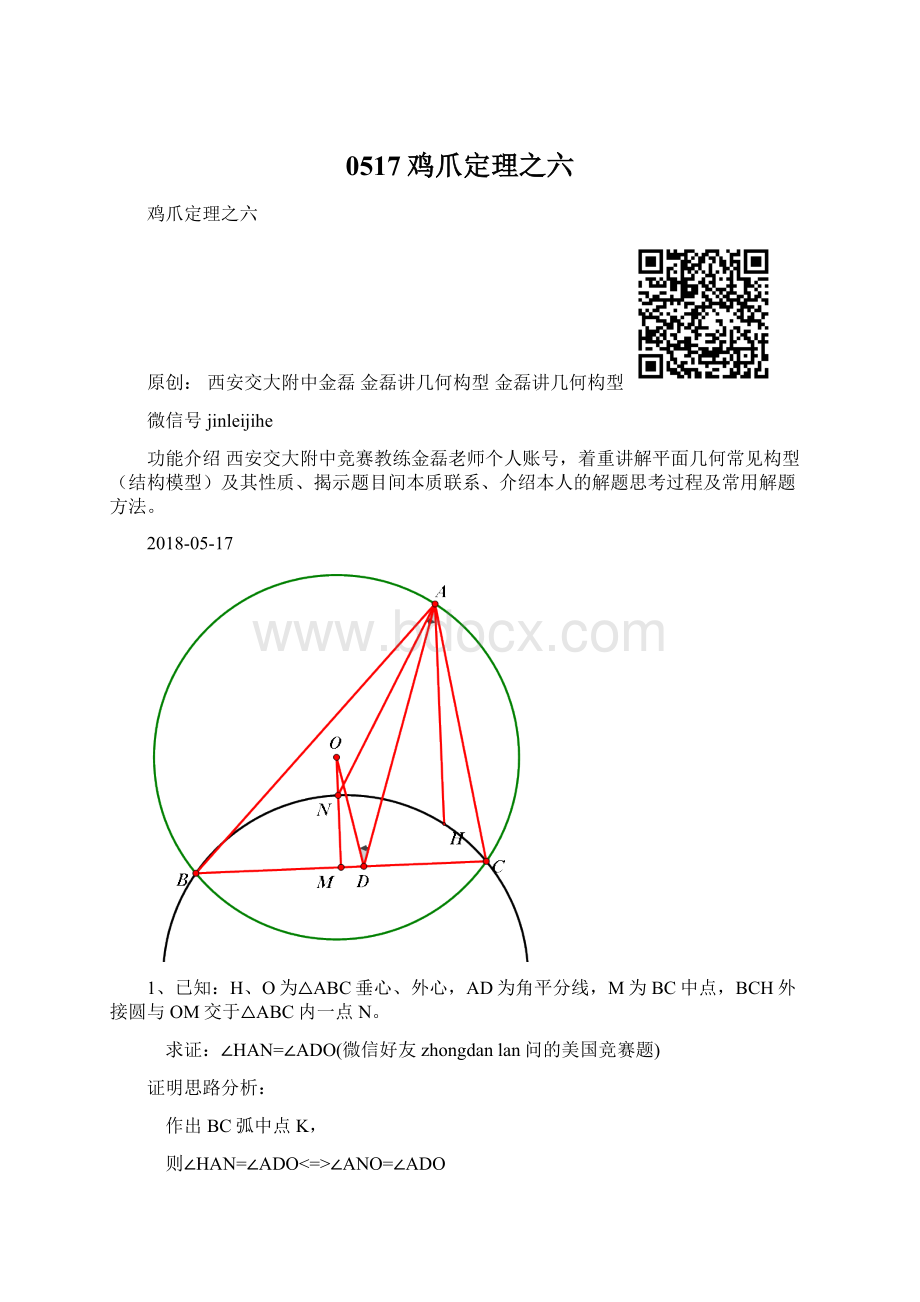
1、已知:
H、O为△ABC垂心、外心,AD为角平分线,M为BC中点,BCH外接圆与OM交于△ABC内一点N。
求证:
∠HAN=∠ADO(微信好友zhongdanlan问的美国竞赛题)
证明思路分析:
作出BC弧中点K,
则∠HAN=∠ADO<=>∠ANO=∠ADO
<=>AOND四点共圆
<=>KN*KO=KD*KA=KB^2(鸡爪定理)
<=>△BKN∼△OBK
<=>∠BKN=∠BNK
<=>∠BNC=∠BKC=180°-∠BAC=∠BHC
<=>BNHC四点共圆
显然成立
注:
本题虽然可以说不用鸡爪定理,不过与它构型本质是相同的。
2、已知:
△ABC内心为I,M、N为AC、AB中点,E、F在AC、AB上,且BE//IM,CF//IN,过I作EF平行线交BC于P.
求证:
P在AI上的射影在△ABC外接圆上(2010年国家队选拔考试)
思路分析:
国家队考试题一般都比较困难,图形繁杂,论述曲折,往往需要多个步骤,层层分析、逐步转化。
本题图形和条件比较复杂,图形比较分散,估计需要一定的计算。
最好分步解决:
1)先确定AE,AF,2)确定∠ATE,3)确定∠IHD,最后用鸡爪定理证明相似从而由同一法得到结果;
证明:
1)设△ABC边、角依次为2a,2b,2c、2x,2y,2z;内切圆半径为1,外接圆O半径R,
设BI交AC于T,I在AB、AC上射影为J、K,AI交圆O于D,过D的AD的垂线交
圆O于H,交BC于Q,∠ATE=θ,∠IHD=β;
由平行及角平分线定理得
TM:
ME=IT:
TB=AT:
AB=CT:
CB=AC:
(AB+BC)=b:
(a+c),
AT=2bc:
(a+c),MT=AT-AM=2bc:
(a+c)-b=b(c-a):
(a+c),
则ME=c-a,AE=a+b-c=CK=cotz,同理AF=BJ=coty。
2)显然∠AFE=θ-x,∠AEF=180°-(θ+x)
△AEF中由正弦定理得coty:
cotz=AF:
AE=sin(x+θ):
sin(θ-x),
即cosysinz:
(coszsiny)=(sinxcosθ+cosxsinθ):
(sinxcosθ-cosxsinθ),
由分比合比定理即得sinxcosθ:
(cosxsinθ)=sin(z-y):
sin(z+y)
又sin(z+y)=cosx,则cotθ=sin(z-y)/sinx。
3)∠HAD=x-(90°-2z)=z-y,
由鸡爪定理得DI=DB=2Rsinx,且∠QID=∠IHD=β,
cotβ=DH/DI=sin(z-y)/sinx=cotθ,
故β=θ,即∠QID=∠PID,故P、Q重合,
即P在AI上的射影在△ABC外接圆上;
注:
1)本题难度不小,主要是条件相对分散,在没有找到良好的性质的条件下,计算也是一个合理的选择;解决问题的关键在于合理分步,蚕食鲸吞、各个击破。
用正弦定理计算出cotθ,对三角函数有一定要求,希望对这方面不熟悉的读者用心体会和揣摩,当然应该还有其他的解法,本人只查到了参考答案的解法,和上述思路类似,不过最后一步他没有利用鸡爪定理,是用梅涅劳斯定理计算得到的,比较而言比上述解法要复杂不少。
2)本题虽然看起来比较困难,但是在熟悉鸡爪定理构型的基础上我看到这个题,就很有信心能解决它。
事实上,这个题目的思路还是比较自然的,计算也不是太复杂。
其实解题时候的信心也是非常重要的因素,当然前提是你对这个基本构型比较熟悉。
3、已知:
如图△ABC内心为I,AI、BI、CI交其外接圆于K、L、M,R在AB上,RP//AK,PB⊥BL,RQ//BL,QA⊥AK。
求证:
MR,QL,PK三线共点(1997年第38届IMO预选题)
思路分析:
图形略复杂,线条较多,我们希望能简化一下图形;如果画出准确图形,不难发现三线所共点还在外接圆上,从而可以删去P点。
只需证明QL与MR交点在外接圆上,要证共圆,必然倒角,需证△AQL∼△ARM,即证△RAQ∼△MAL,这由鸡爪定理及平行不难得到;
证明:
设QL交MR于T,
设QA交CI于N,由鸡爪定理得ANBI共圆且M为其圆心,
且LI=LA,MI=MA,故LM为AI中垂线,
则QA//LM,又RQ//BL,则∠AQR=∠MLB=∠MLA,
∠QRA=∠LBA=∠LMA,
则△RAQ∼△MAL,
则QA/LA=RA/MA,故△AQL∼△ARM,
则∠QLA=∠RMA,
故LAMT共圆,则T为MR与外接圆的交点;
对称的,PK也过T,从而MR,QL,PK三线共点。
注:
本题看着挺吓人,其实只要沉着应战,适当简化,步步紧逼,得到答案不算困难。
当然本图形中还蕴含着一些有趣的结论,例如研究此圆圆心轨迹等等。
4、已知:
O,I为△ABC外心和A-旁心,P为AI中点,AI交BC于D,IT⊥BC于T,O'为△ATD外心。
求证:
O'OP共线;
分析:
把两圆补出来合情合理,设两圆另一交点为Z,共线等价于IZ⊥AZ,联想到此类构型的核心性质即可;
证明:
设AI交圆O于K,KT交圆O于Z,
由第一篇文章中命题2知KI^2=KD*KA=KT*KZ,
则ZTDA共圆,且∠TID=∠KZI,
又∠IDT=∠KZA,则IZ⊥AZ,
则OO'//IZ,又OO'为AZ中垂线,
故O'OP共线;
注:
两个外心提示作出外接圆,两圆相交公共弦是关键。
本题把核心性质应用的淋漓尽致,如果思路跑偏,会枉费许多心血。
5、已知:
△ABC内心为I,BI交其外接圆于M,AB>AC,∠AOB,BOC角平分线交以BM为直径的圆于P、Q,R在QP上且RB=RM。
求证:
RB//AC(2014年第55届IMO预选题3)
思路分析:
RB//AC<=>∠RBM=∠AZM=∠BAM=∠BOL
<=>LQ^2=LB^2=LP^2=LO*LR<=>LQPO共圆,
这样就能R消掉且能把以BM为直径的圆消掉.
原题简化为:
如上图,∠ABC角平分线交△ABC外接圆O于M,
L为BM中点,OP⊥AB,OQ⊥CB,LP=LQ=LB,
求证:
POLQ共圆。
百尺竿头更进一步,圆和△ABC都能消掉,进一步转化为如上图OP⊥XB,OQ⊥YB,LP=LQ=LB,
∠XBL=∠LBY;
在这么简答的图形下,结果就水落石出,唾手可得了。
证明:
显然BXOLY共圆,LX=LY,LP=LQ,∠OXL=∠LYO,
则△LXP≅△LYQ(因为两边和一个钝角对应相等,两三角形全等)
则∠XPL=∠YQL,则POLQ共圆,
则原结论成立。
注:
1)本题不是太难,但是图形初看比较复杂,而且这种以BM为直径的圆的构型比较罕见,上手时会很有压力。
以上不厌其烦的详细还原了本人解题过程,就是不停的简化图形和转化图形,经过三次简化,最后在简洁的图形下,结论变得显而易见,而且似乎还能推广。
希望初学者认真体会。
2)本题再次用到了SSA判定,其中若对应角为钝角,则两三角形全等,这个用几何方法或者正弦定理都是显然的。