第4章支路电流法.docx

第4章支路电流法.docx

《第4章支路电流法.docx》由会员分享，可在线阅读，更多相关《第4章支路电流法.docx（19页珍藏版）》请在冰豆网上搜索。

第4章支路电流法

支路电流法

说明：

这是电工学课程直流电路章节中的一小节，故所用例题均为直流电路。

但支路电路法其实适用于任何电路的分析，是电路分析的基本方法。

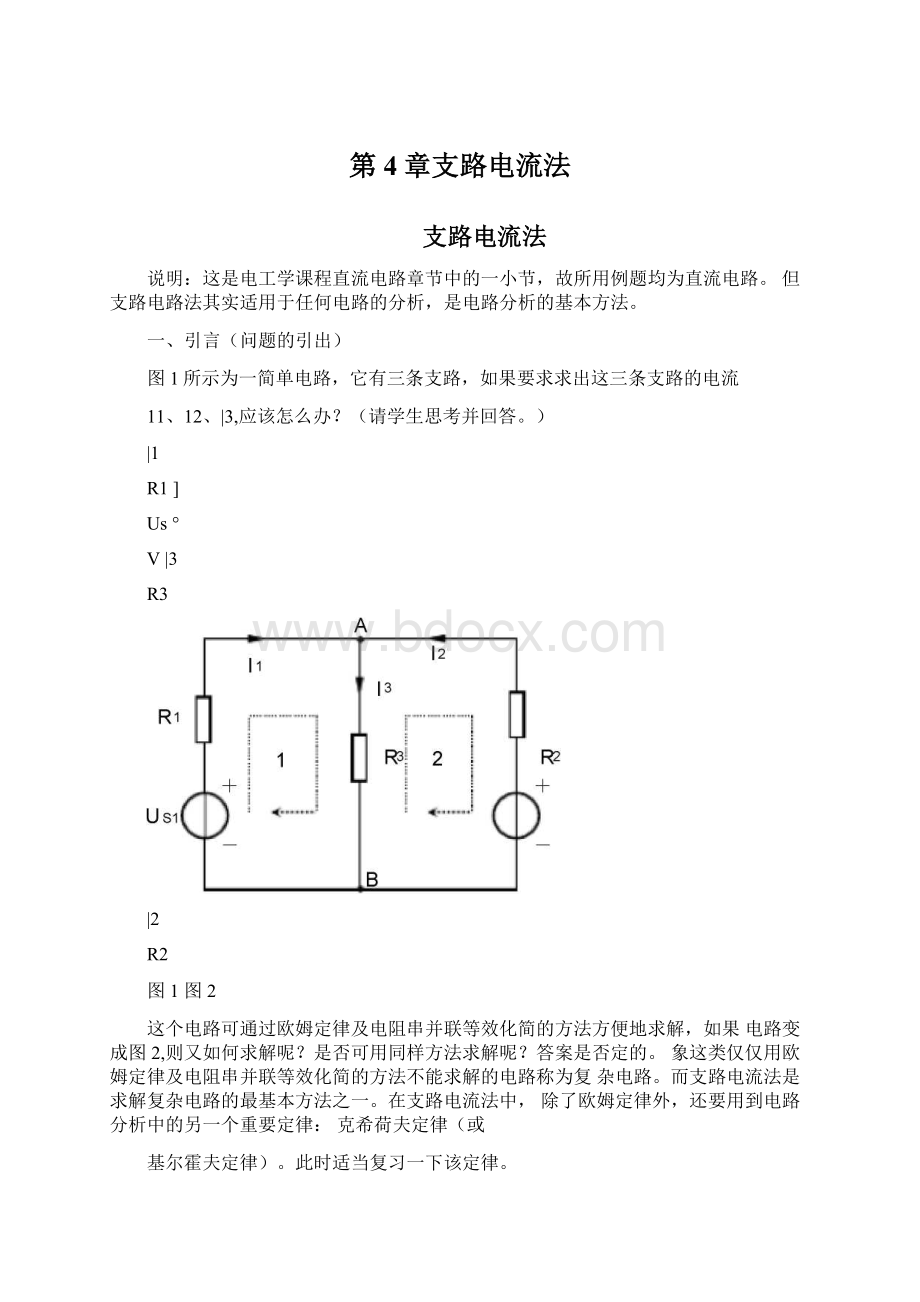
一、引言（问题的引出）

图1所示为一简单电路，它有三条支路，如果要求求出这三条支路的电流

11、12、|3,应该怎么办？

（请学生思考并回答。

）

|1

R1]

Us°

V|3

R3

|2

R2

图1图2

这个电路可通过欧姆定律及电阻串并联等效化简的方法方便地求解，如果电路变成图2,则又如何求解呢？

是否可用同样方法求解呢？

答案是否定的。

象这类仅仅用欧姆定律及电阻串并联等效化简的方法不能求解的电路称为复杂电路。

而支路电流法是求解复杂电路的最基本方法之一。

在支路电流法中，除了欧姆定律外，还要用到电路分析中的另一个重要定律：

克希荷夫定律（或

基尔霍夫定律）。

此时适当复习一下该定律。

二、支路电流法

支路电流法：

以电路中的支路电流作为待求量，应用基尔霍夫电流定律

（KCL）和基尔霍夫电压定律（KVL）分别对节点和回路列出所需要的方程电流。

支路电流求出后，其它电量就很容易得到。

下面用支路电流法计算图2电路的电流|1、|2、|3。

1、为了求解图2电路的3个支路电流|1、12、|3，首先标出各个电流的正方向，并明确应该列出3个互相独立的方程才能求解。

问题是这三个方程怎么列？

2、用克希荷夫定律列方程

（1）先用KCL对节点列出方程（称节点电流方程）。

该电路有2个节点，设

为A、B。

对节点A有：

丨1+|2-|3=0

（1）

对节点B有：

-l1-|2+|3=0

（2）

显然两式不独立，所以用

KVL可列出1个独立方程，现选

（1）式。

般地，对于有n个节点的电路，只能列出n-1个独立电流方程。

⑵然后用KVL列出所需要的另二个方程（注意是独立方程），称回路电压

方程。

（该电路共有三个回路）

⑶

⑷

（5）

选择二个回路，并设定其绕行方向如图所示。

对回路1应用KVL，得：

IiRi+|3R3-Usi=0对回路2应用KVL，得：

-I2R2-I3R3+Us2=0若再对回路3列方程：

Usi-IiRi+l2R2-Us2=0

很显然，该式是前二式的线性组合，不是独立方程，这样，用KVL列出

了2个相互独立的方程（3）和（4），当然也可以是（4）、（5）或（3）、（5）。

这样便得到了3个独立方程式

（1）、（3）、（4）组成的方程组。

注意，在用KVL列回路电压方程时，为了列出b-（n-1）独立的方程，一

般在选回路时，要使所选的每个回路至少包含一条已选回路所没有的新支路，这样便可保证列出的每个电压方程相互独立，一般可选网孔作为列KVL

方程时的回路。

网孔：

几个相邻支路围成的最简单回路，例如图2中的回路1、回路2

就是网孔。

3、解该方程组，便得：

US1（R2R3）US2R3

1

R1R2

R2R3

R3R1

R1R2

R2R

R3Ri

US1R3

u

S2（R1

R3）

RR2

R2R3

R3R

R-iR2

R2R3

R3R

US1R2

US2R1

RR2

R2R3

R3R

R1R2

R2R3

R3R1

根据计算的正负号与假设的正方向相比较，即可得到各支路电流的实际方向。

一般地，对于有b条支路、n个节点的电路，用KCL一定可列出n-1个独立节点电流方程，用KVL一定可列出还需的b-（n-1）个独立回路电压方程，共是n个独立方程，从而可求解b条支路的支路电流。

这个结论的证明可参考

见有关电路理论书籍。

综上所述，可归纳出支路电流法的一般分析步骤如下：

a.分析电路有几条支路（设有b条），几个节点（设有n个），并标出电流正方向。

b.用KCL对节点列出n-1个独立节点电流方程。

c.选定合适回路，用KVL对回路列出另外所需的b-（n-1）个独立的回路电压

联立解之，可得li=-5A,|2=5A列回路电压方程时，应避开含电流源支路。

、结束语

用支路电流法分析电路时，若遇到支路数较多的电路，贝懦要列出的独立方程数也多，例如10个或20个，解方程组时就比较麻烦，虽说可用计数机辅助求解，但这时可考虑采用别的电路分析方法，如电压源电流源等效互换法、节点电压法等等，对于不同的电路，可采用相对合适的分析方法。

做到灵活应用所学的知识。

四、作业

1.见教材

2.自学节点电压法，下次课抽查。

电路中电位的计算

电位：

选定电路中某一点作为参考点，并规定该点电位为零值。

则任一点至

参考点之间的电压即为该点的电位值。

电位用V表示，单位：

伏（V）

［讲解时可根据式Uab=Va-Vb引出电位物理量。

Va、Vb到底是多少？

怎么计算呢？

以引起注意然后可举例类比如海拔高度等概念，以获取对电位概念的电位计算步骤：

1.先选定电路中某一点作为参考点，并设该点电位为零值。

参考点的选择以简化电路计算为原则。

一般选电路的公共端，参考点以“丄”符号标记，常称为“地”端，但实际上它并不一定与大地相联。

2.某点的电位等于该点至参考点之间的电压。

这样，电位计算实际上就是电压的计算，可用各种电路分析方法求得。

电位值与参考点的选择有关，而与该点至参考点的路径无关。

计算某点电位，只要从该点出发通过任一路径（以简化解题为原则）绕到参考点，该点电位就是等于此路径上全部电压之代数和。

小结：

1.电位概念

2.电位计算

3.电位特点：

与参考点的选择有关，而与该点至参考点的路径无关。

电位值是唯一的。

4.任二点间的电压等于该两点的电位差：

设0为参考点，贝UVa=Uao

Vb=UboVa-Vb=Uao-Ubo=Uab（根据KVL）

电位正负值意义：

J某点电位为正，表示该点电位比参考点高

电位为负，表示该点电位比参考点低

电位计算举例：

计算下图a、b、c、d四点的电位。

（1）以b作参考点

（2）以a作参考点

解：

（1）以b作参考点

Vb=0Va=I3R3

⑵以a作参考点

Va=0Vb=-|3R3

Vc=EVd=E2

Vc=11R1Vd=I2R2

①参考点一旦选定，电位值唯一

可见

②参考点选择不同，各点电位随之改变电子线路简便画法：

用点位值代替理想电压源：

如:

R1

R3

1

R2

请几位学生做下题:

题1：

求下图所示电路中a、b、c点的电位。

I1Q

32807V

Vb

8V

Vc

0V

题2：

Vi=3V

2kr1

10k

J

-6V

求b点电位Vb

解:

VaVi3v

Vc6V

•,UacVaVc3.…IA

4

3

•••VbUbcVc1061.5V

4

作业：

学习指导书P19.1-6

叠加原理

。

等于各个电

原理：

在线性电路中，若有多个电源，则电路中任一支路上的电流（或电压）

源单独作用时在该支路上产生的电流（或电压）之代数和。

L

R2

US单独作用

Q

3.电流、电压可叠加，功率不能叠加。

4.应用叠加原理，能简化电路计算。

以上图为例说明叠加原理的应用

例1.用叠加原理计算上图各支路电流I1、I2、I及电压U，并计算电阻R上消

耗的功率。

解：

⑴画好各电流、电压正方向

⑵求电压源单独作用时各支路电流及电压

⑶求电流源单独作用时，各支路电流及电压

厂12Is10A

IIs0.55A

II5A

Lu5v

⑷求总的支路电流

厂III7.5512.5a

I1I1I17.552.5A

Y

I2I2I210A

-UUU12.5A

（5）计算R上的功率

PRIR12.521

2

而PRI1R7.521

PRI1R521

显然PR

既功率不能叠加。

例2.已知⑴—1VE21V时U30VHl-

线性_

电阻U3

电路'

E2

⑵U110VE20V时u31V+j—

求u10VE210VU3?

—

解：

设610VE20（即510V单独作用）时U3XU10V

E210VU3Y

根据已知条件

（2）有X1V

根据已知条件

（1）有XY0

•••YX1V

即U1

0V

E210V时

U3

1V

例3.

用叠加原理计算a点电位：

200VJ一

15K

L

I

15K

4

I

15K

■■11

—r

a匸

L°

a200V厂

10K

10K

+

10K

]

-100V

-100V

解：

当

当100/单独作用时:

I-

100

4mA

25K

Va

I15K

415

60V

当200V单独作用时：

I

200

8mA

25K

Va

I10K810K80V

•-Va

VaVa20V

或2

II4812mA

•-Va

I10K100V121010020V

作业：

见教材

等效电源定理

问题的提出：

只要求计算一条支路上电流时，用等效电源定理分析电路，则较为简单。

对外等效概念：

当两个二端网络在任一时刻对外输出的电流和电压相等时，我们就说它们是互为等效的。

在介绍等效电源定理之前，先解释几个电路名词。

几个名词：

网络：

电路的泛称。

二端网络：

只有二个出线端的网络。

无源二端网络：

二端网络内不含电源。

如有源二端网络：

二端网络内包含电源。

等效电源定理是描述有源二端网络的包括等效电压源定理和等效电流源定理。

一、等效电压源定理（戴维南定理）

定理：

对于任一线性有源二端网络，就其对外作用来说，可以用一个电动势E0或电压U0内

阻Ro相串联的电压源来等效。

其中Eo的值等于该二端网络的开路电压U。

，内阻Ro的值

等于把该网络内部除源后，该网络的入端电阻。

b

对外等效

RL

应用：

若要计算复杂电路中某一支路电流时，先将这一支路移去，留下的部分即为一个有

Rorl

源二端网络，根据戴维南定理将其等效化简，则待求支路电流为

等效电源的Us、Ro可通过实验或计算得出。

关键：

应用戴维南定理的关键是如何求us、Ro

（1）求Us:

可应用前面的KCL、KVL，支路电流法、节点电位法（自学）等等方法,

还可用实测方法测定。

（2）求Ro:

（a）网络除源后，应用电阻的串并联法。

（b）网络除源后，在网络端口上外加电压U，有电流表测得电流I

Ro%。

（c）网络端口的开路电压Uo除以网络端口的短路电流Is

Ro%

（d）负载试验法：

将已知

Rl接至有源网络输出端，则

Ul

Us

Rl

Rorl

Ro（氏1）Rl

Ul

注意事项：

应用戴维南定理时应注意如下几点:

1.电源除源指独立（理想）电压源短路独立（理想）电流源开路。

2.戴维南等效电路只对外等效。

二端网络内部电路一般不等效。

3.只应用于线性电路。

4.在等效电路中，注意Us的极性应与开路电压U。

的极性一致。

例:

ioQ

线性有源二端网络

a

■4-

20V

R

已知ab开路电压为6OV,

ab短路电流3A。

求R2O时，R上流过的电流?

解：

（1）将ab左边的电路根据戴维南定理化简成等效电压源

（2）求Us60V

•••短路电流为ls3A又Is

Ro

•-Ro土2o

1s

和内阻Ro并联的电源来等效代替，等效电源的电流Is就是有源二端网络的短路电

流，等效电源的内阻Ro等于有源二端网络中所有电源除去（理想电压源视为短路、

理想电流源视为开路）后端口的入端电阻。

例：

分别应用戴维南定理和诺顿定理将下图各电路化为等效电压源和等效电流源的形式:

（b）

作业：

学习指导书P19115113

受控源

1•定义：

电压源的电压或电流源的电流，受电路中其它部分的电流或电压控制。

这种电源称受控源。

当控制的电压或电流消失或等于零时，受控电源的电压或电流也将为零。

②电压控制电流源g乂转移电导

Ui

③电流控制电压源r丄°转移电阻

④电流控制电流源

学电流比或电流放大倍数

3•符号:

电压控制

理想情况

电流控制

理想情况：

Ri=0③CCVS

4•理想受控源：

（不讲）

电压控制的理想受控源：

Ri

;输出端为理想电流源或电压源。

5.举例

①P321—27

方法一对节点a：

厂Ii-U2

6

I2

厂Ii丄U2

6

-U2

3

U2

I2

Ii2

IU282Ii

方法二：

用戴维南定理做。

U2

U2

6V

Ii

I2

1A

2A

R3

a

L+

Us

求：

Us;求：

Rs

1

Uabo*3Uabo

6

对节点a列RCL:

Ii

~3

即li

IU2

6

.Ii2Us

IiRs8

8li=8

Ii=1

U2UsIiRs016

6V

②1—28题

（请二位学生做）

10V

（画出求

Us的等效电路图）

求Is：

求Ro：

3

.Uabo20V

.•.Is

（求Ro另一方法:

除源后:

b）求Us

Uabo

5.4

I6（2

I）

3I

12

2

10…

1

一I

—

5A

Uabo310V

3.6

3

3

•Us

Uabo

10

310V

3

求Is：

相应电路为

Is

I=0•••受控电压源的电压为5.4I=0

求Ro：

戴维南等效电路为

b

其中Us

10V

1.叠加原理作用与线性电路：

由线性元件组成的电路称线性电路。

线性元件特征：

其特

性曲线是线性的，既直线，如电阻伏安特性u2R。

电压源外特性UEIR0。

若它们是线性电阻和线性电源。