C语言图形输出习题.docx
《C语言图形输出习题.docx》由会员分享,可在线阅读,更多相关《C语言图形输出习题.docx(28页珍藏版)》请在冰豆网上搜索。
C语言图形输出习题
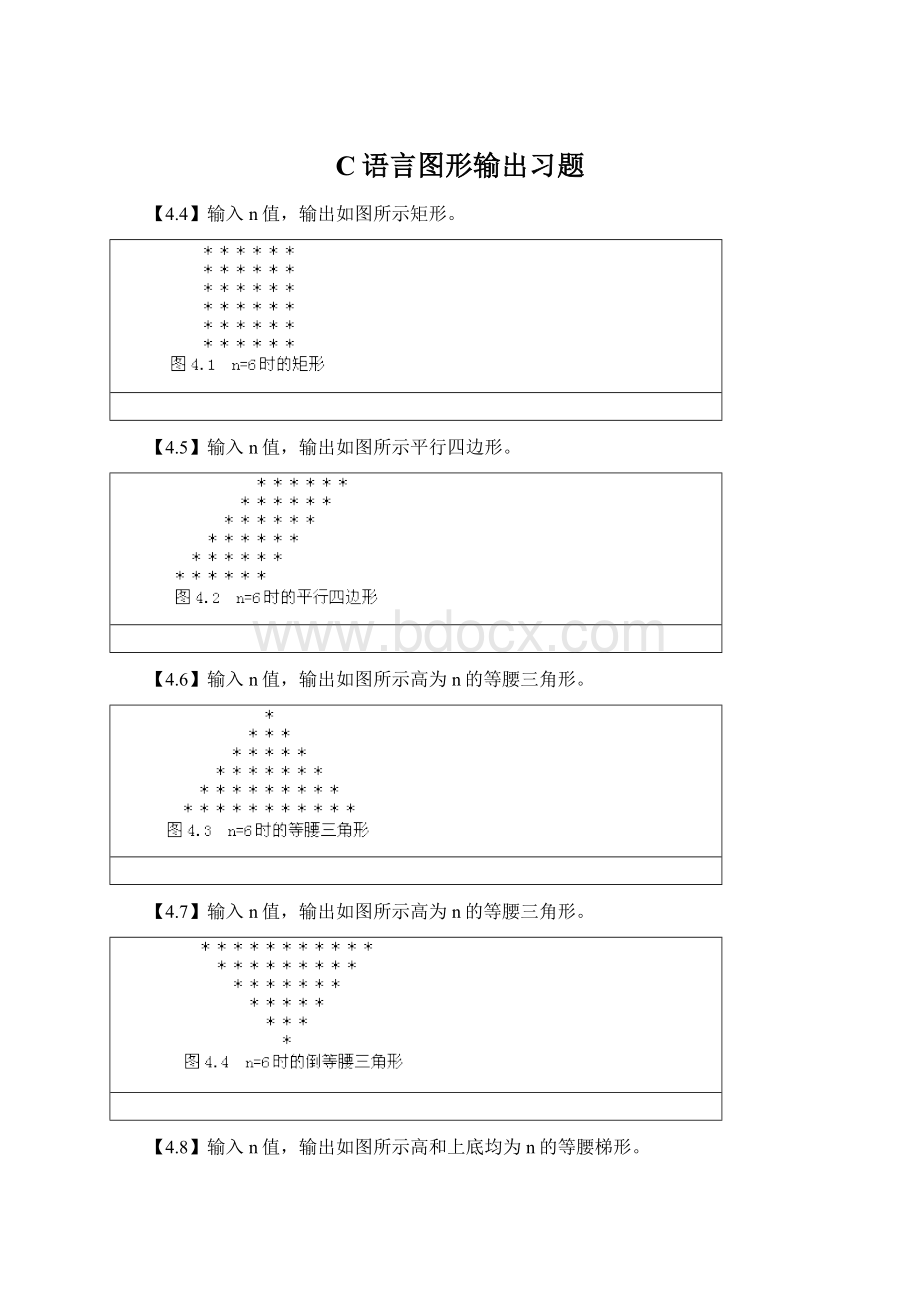
【4.4】输入n值,输出如图所示矩形。
【4.5】输入n值,输出如图所示平行四边形。
【4.6】输入n值,输出如图所示高为n的等腰三角形。
【4.7】输入n值,输出如图所示高为n的等腰三角形。
【4.8】输入n值,输出如图所示高和上底均为n的等腰梯形。
【4.9】输入n值,输出如图所示高和上底均为n的等腰空心梯形。
【4.10】输入n值,输出如图所示边长为n的空心正六边型。
【4.11】输入n值,输出如图所示图形。
【4.12】输入n值,输出如图所示图形。
【4.13】输入n值,输出如图所示图形。
【4.14】输入n值,输出如图所示图形。
【4.15】输入n值,输出如图所示图形。
【4.16】输入n值,输出如图所示图形。
(例为n=6时)
【4.17】编写程序,输出如图所示sin(x)函数0到2π的图形。
【4.18】编写程序,在屏幕上输出一个由*号围成的空心圆。
【4.19】编写程序,在屏幕上绘制如图余弦曲线和直线。
若屏幕的横向为x轴,纵向为y轴,在屏幕上显示0~360度的cos(x)曲线与直线x=f(y)=45*(y-1)+31的迭加图形。
其中cos图形用"*"表示,f(y)用"+"表示,在两个图形的交点处则用f(y)图形的符号。
【4.20】编写程序,输出如图所示高度为n的图形。
【4.21】编写程序,输出如图所示高度为n的图形。
【4.22】输入n值,输出如图所示图形。
【4.23】输入n值,输出如图所示的n×n(n<10)阶螺旋方阵。
12345
161718196
152425207
142322218
131211109
图4.19n=5时的螺旋方阵
【4.24】输入n值,输出如图所示回型方阵。
【4.25】输出如图所示的数字金字塔
【4.26】输入n值,输出如图所示图形。
【4.27】输入顶行字符和图形的高,输出如图所示图形。
【4.28】输入首字符和高后,输出如图所示回型方阵。
AAAAA
ABBBA
ABCBA
ABBBA
AAAAA
图4.24首字符为'A'、高为5的方阵
【4.29】输入中心字符和高后,输出如图所示回型方阵。
XXXXX
XYYYX
XYZYX
XYYYY
XXXXX
图4.25中心字符为'Z'、高为5的方阵
【4.30】编写程序,输出如图所示上三角形式的乘法九九表。
【4.31】编写程序,输出如图所示下三角乘法九九表。
【4.4】分析:
打印此图形用两重循环实现。
图形要重复n行,故采用循环结构实现循环n次,循环体内部打印一行'*'号,把上述思路表示为:
for(i=1;i<=n;i++)
打印一行'*'号;
每行有n个'*'号,再采用循环结构实现n次循环,循环内部用格式输出语句打印一个'*'号,即:
for(j=1;j<=n;j++)
printf("*");
按照上述思路,实现打印矩形。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++)
printf("*");
printf("\n");
}
}
【4.5】分析:
此图形和上题的区别在于在每一行先要打印空格,然后再打印n个'*'号,在上题第一层循环体内打印'*'号的循环前面增加一个循环打印空格。
每行空格的个数是逐行减少的,由于第一层循环的控制变量i是逐行增1,所以用一个固定值的数减去i就可实现对空格个数的控制,在此题中固定值可使用变量n。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n-i;j++)
printf("");
for(j=1;j<=n;j++)
printf("*");
printf("\n");
}
}
【4.6】分析:
此题和上题的区别在于每行'*'的数量逐行减少,可以使用上题控制空格个数的思路来控制'*'号的个数,请注意每行'*'的个数都是奇数。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n-i;j++)
printf("");
for(j=1;j<=2*i-1;j++)
printf("*");
printf("\n");
}
}
【4.7】分析:
此题图形是第3题图形的垂直反转,在编程上我们可以变换一个思路。
对于图形中的第i行(1≤i≤n),共需要输出2n-i个字符,其中前面的i-1个字符为空格,后面的字符为'*'号。
按照这一思路可以编写出如下程序。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)/*重复输出图形的n行*/
{for(j=1;j<=2*n-i;j++)/*重复输出图形一行中的每个字符*/
if(j<=i-1)printf("");/*输出前面的空格*/
elseprintf("*");/*输出后面的*号*/
printf("\n");
}
}
【4.8】分析:
此题和第3题的区别仅是每行的'*'个数增加n-1个。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n-i;j++)
printf("");
for(j=1;j<=2*i-1+(n-1);j++)
printf("*");
printf("\n");
}
}
【4.9】分析:
对于空心图形,我们可以在上题的基础上,对于打印'*'号的循环进行修改,仅在循环开始值(j=1)和循环结束值(j=2*(i-1)+n)时打印'*'号,其它位置都打印空格。
另一种思路是将每行打印的空格和'*'的两个循环合为一体考虑,在判断出需要打印'*'的两个位置及第一行和最后一行相应位置外,其余位置都打印空格。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=2*n+i-3;j++)
if(j==n-i+1||j>n-i+1&&(i==1||i==n))printf("*");
elseprintf("");
printf("*\n");
}
}
【4.10】分析:
此图形可以理解为两个空心梯形反向连接而成,因此可以利用上题的思路进行输出。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)/*输出图形的上半部分(含中心行)*/
{for(j=1;j<=2*n-i-1;j++)
if(j==i)printf("*");
elseprintf("");
printf("*\n");
}
for(i=1;i{for(j=1;j<=n+i;j++)
if(j==n-i)printf("*");
elseprintf("");
printf("*\n");
}
}
【4.11】分析:
此题与上题的区别在于打印'*'号的位置不同,编程时要找出应打印'*'号的位置和两个循环变量i、j以及行数n的关系。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)/*输出图形的上半部分(含中心行)*/
{for(j=1;j<=2*n-i;j++)
if(j==n-i+1||j>n-i+1&&i==1)printf("*");
elseprintf("");
printf("*\n");
}
for(i=1;i{for(j=1;j<=3*(n-1)-i;j++)
if(j==i+1||j>i+1&&i==n-1)printf("*");
elseprintf("");
printf("*\n");
}
}
【4.12】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++)
if(j==n-i+1||i==1||i==n)printf("*");
elseprintf("");
printf("\n");
}
}
【4.13】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)/*输出图形的上半部分(含中心行)*/
{for(j=1;j<=n-i;j++)
if(j==1||j==n-i+1)printf("*");
elseprintf("");
printf("\n");
}
for(i=1;i{for(j=1;j<=i+1;j++)
if(j==1||j==i+1)printf("*");
elseprintf("");
printf("\n");
}
}
【4.14】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++)
if(j==1||j==i||j==n)printf("*");
elseprintf("");
printf("\n");
}
}
【4.15】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n+i-1;j++)
if(j>n-i)printf("*");
elseprintf("");
printf("\n");
}
for(i=1;i{for(j=1;j<=2*n-i-1;j++)
if(j>i)printf("*");
elseprintf("");
printf("\n");
}
}
【4.16】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n+i-2;j++)
if(j==n-i+1)printf("*");
elseprintf("");
printf("*\n");
}
}
【4.17】分析:
首先对图形进行设计,坐标的X轴和Y轴分别对应屏幕的列和行,一个正弦函数的周期为0~360度,我们把一个步长定义为10度,打印时每换一行等于函数的自变量增加10度;屏幕的列宽为80,函数值为0对应屏幕的第40列,sin(x)的值在-1~1,变换成列数为以0为中心的-30~30,对应屏幕上第10~70列。
设计程序时,控制换行的自变量i乘以10得到正弦函数的X值,调用库函数sin()求出函数值再乘以30输出的列宽,因为我们以屏幕的第40列为0点,故再加上40得到应在屏幕上显示的点。
参考答案:
#definePAI3.14159
#include
main()
{doublex;
inty,i,yy;
for(i=1;i<80;i++)/*打印图形的第一行*/
if(i==40)printf("*");/*i控制打印的列位置*/elseprintf("-");
printf("\n");
for(x=10.0;x<=360.0;x+=10.)/*从10度到360度*/
{y=40+30*sin(x*PAI/180.0);/*计算对应的列*/
yy=40>y?
40:
y;/*下一行要打印的字符总数*/
for(i=1;i<=yy;i++)/*控制输出图形中的一行*/
{if(i==y)printf("*");/*i控制打印的列位置*/
elseif(i==40)printf("|");/*打印中心的竖线*/
elseprintf("");
}
printf("\n");
}
}
【4.18】分析:
首先设计屏幕图形,如果预计圆形在屏幕上打印20行,所以定义圆的直径就是20,半径为10,圆的方程是X2×Y2=R2,因为图形不是从中心开始打印而是从边沿开始,所以Y从10变化到-10,根据方程求出X,对求得的X值再根据屏幕行宽进行必要的调整得到应打印的屏幕位置。
参考答案:
#include
main()
{doubley;
intx,m;
for(y=10;y>=-10;y--)/*圆的半径为10*/
{m=2.5*sqrt(100-y*y);/*计算行y对应的列坐标m*/
for(x=1;x<30-m;x++)
printf("");/*输出圆左侧的空白*/
printf("*");/*输出圆的左侧*/
for(;x<30+m;x++)
printf("");/*输出圆的空心部分*/
printf("*\n");/*输出圆的右侧*/
}
}
【4.19】参考答案:
#include
#include
main()
{doubley;
intx,m,n,yy;
for(yy=0;yy<=20;yy++)
{y=0.1*yy;
m=acos(1-y)*10;
n=45*(y-1)+31;
for(x=0;x<=62;x++)
if(x==m&&x==n)printf("+");
elseif(x==n)printf("+");
elseif(x==m||x==62-m)printf("*");
elseprintf("");
printf("\n");
}
}
【4.20】分析:
编程的关键为两点,一是使用控制输出的行和列,这方面的内容在前面已经叙述,另一点是输出的数字和所在行、列关系。
此题第一行输出的数字恰好是列数,从第二行起每行的数字均比上一行增n。
参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++)
printf("%4d",(i-1)*n+j);
printf("\n");
}
}
【4.21】分析:
此题的关键是找到输出数字和行、列数的关系。
审查图形中每行中数字的关系发现,右边数字和前面数字之差逐次增1;同列数字依然是这样的关系,编程的关键转换为找到每一行左方的第一个数字,然后利用行和列的循环变量进行运算就可得到每个位置的数字。
用ai,j此表示第i行第j列的数字,则a11=1;由第i行第一列的数字推出第i+1行第一列的数字是ai+1,1=ai,1+i;同样由第j列推出第j+1列的数字是ai,j+1=ai,j+i+j。
另外只有当j参考答案:
main()
{inti,j,m,n,k=1;/*k是第一列元素的值*/
printf("Pleaseenterm="");
scanf("%d",&m);
for(i=1;i<=m;i++)
{n=k;/*n第i行中第1个元素的值*/
for(j=1;j<=m-i+1;j++)
{printf("%3d",n);
n=n+i+j;/*计算同行下一个元素的值*/
}
printf("\n");
k=k+i;/*计算下一行中第1个元素*/
}
}
【4.22】参考答案:
main()
{inti,j,n;
printf("\nPleaseEntern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++)
if(j<=i)printf("1");
elseprintf("%3d",j-i+1);
printf("\n");
}
}
【4.23】分析:
可用不同的方案解决此问题,为了开阔读者的思路,这里给出了两个参考答案,其中第二个答案是使用了递归方法。
方案一:
首先寻找数字输出数字和行列的关系。
每圈有四个边,把每边的最后一个数字算为下边的开始,最外圈每边数字个数是n-1个,以后每边比外边一边少两个数字。
因为数字是一行一行输出的,再分析每行数字的规律。
实际没有的数字有三种规律:
位于对角线之间的数字是上半图增一,下半图减一。
对角线左侧的各列,右侧比左侧增加了一圈数字,例如数字39和它左侧的22比较,数字39所在的圈每边4个数字,左侧22加上一圈16个数字在加1就是39。
同理,对角线右侧的各列,则减少一圈的数字个数。
根据以上分析,用两个对角线将图形分为四个区域,如下图所示,图中黑斜体字为对角线上的数字。
1234567
2425262728298
2340414243309
22394849443110
21384746453211
20373635343312
19181716151413
为叙述方便我们称四个区域为上、下、左、右区。
设i、j为行列号,n为图形的总行数,则满足各区的范围是,上区:
j>=i且j<=n-i+1;下区:
j<=i且j>=n-i+1;左区:
jj>i且j>n-i+1。
现在问题是,如果知道一行在不同区域开始第一个位置的数字,然后该区后续的数字就可利用前面分析的规律得到。
对于右区开始各行第一个数字最易求出,为4*(n-1)-i+1。
后续一个和同行前一个数字之差是4*[n-1-(j-1)*2]+1,其中方括号内是每边的数字个数。
对角线上的数字是分区点,对角线上相临数字仍然相差一圈数字个数,读者自行分析得到计算公式。
右区开始的第一个数字可以从上区结束时的数字按规律求出。
下述程序用变量s保存分区对角线上的数字。
参考答案一:
main()
{inti,j,k,n,s,m,t;
printf("Pleaseentern:
");
scanf("%d",&n);
for(i=1;i<=n;i++)
{s=(i<=(n+1)/2)?
1:
3*(n-(n-i)*2-1)+1;
m=(i<=(n+1)/2)?
i:
n-i+1;/*m-1是外层圈数*/
for(k=1;kfor(j=1;j<=n;j++)
{if(j>=n-i+1&&j<=i)/*下区*/
t=s-(j-(n-i))+1;
if(j>=i&&j<=n-i+1)/*上区*/
t=s+j-i;
if(j>i&&j>n-i+1)/*右区*/
t-=4*(n-2*(n-j+1))+1;
if(j{if(j==1)t=4*(n-1)-i+2;
elset+=4*(n-2*j+1)+1;
}
printf("%4d",t);
}
printf("\n");
}
}
方案二:
根据本题图形的特点,我们可以构造一个递归算法。
我们可以将边长为N的图形分为两部分:
第一部分最外层的框架,第二部分为中间的边长为N-2的图形。
对于边长为N的正方型,若其中每个元素的行号为i(1≤i≤N),列号为j(1≤j≤N),第1行第1列元素表示为a1,1(a11=1),则有:
对于最外层的框架可以用以下数学模型描述:
上边:
a1,j=a1,1+j-1(j≠1)
右边:
ai,N=a1,1+N+i-2(i≠1)
下边:
ai,1=a1,1+4N-i-3(i≠1)
左边:
aN,j=a1,1+3N-2-j(j≠1)
对于内层的边长为N-2的图形可以用以下数学模型描述:
左上角元素:
ai,i=ai-1,i-1+4(N-2i-1)(i>1)
若令:
ai,j=fun(ai-1,i-1+4(N-2i-1),当:
i<(N+1)/2且j<(N+1)/2时,min=MIN(i,j),则有:
a2,2=fun(a1,1,min,min,n)
ai,j=fun(a2,2,i-min+1,j-min+1,n-2*(min-1))
我们可以根据上述原理,分别推导出i和j为其它取值范围时的min取值。
根据上述递归公式,可以得到以下参考程序。
参考答案二:
#include
#defineMIN(x,y)(x>y)?
(y):
(x)
fun(inta11,inti,intj,intn)
{intmin,a22;
if(i==j&&i<=1)return(a11);
elseif(i==j&&i<=(n+1)/2)return(fun(a11,i-1,i-1,n)+4*(n-2*i+3));
elseif(i==1&&j!
=1)return(a11+j-1);