中考数学压轴题冲刺提升专题12击破类比探究类综合题利器之全等知识.docx

中考数学压轴题冲刺提升专题12击破类比探究类综合题利器之全等知识.docx

《中考数学压轴题冲刺提升专题12击破类比探究类综合题利器之全等知识.docx》由会员分享，可在线阅读，更多相关《中考数学压轴题冲刺提升专题12击破类比探究类综合题利器之全等知识.docx（34页珍藏版）》请在冰豆网上搜索。

中考数学压轴题冲刺提升专题12击破类比探究类综合题利器之全等知识

专题12击破类比、探究类综合题利器之全等知识

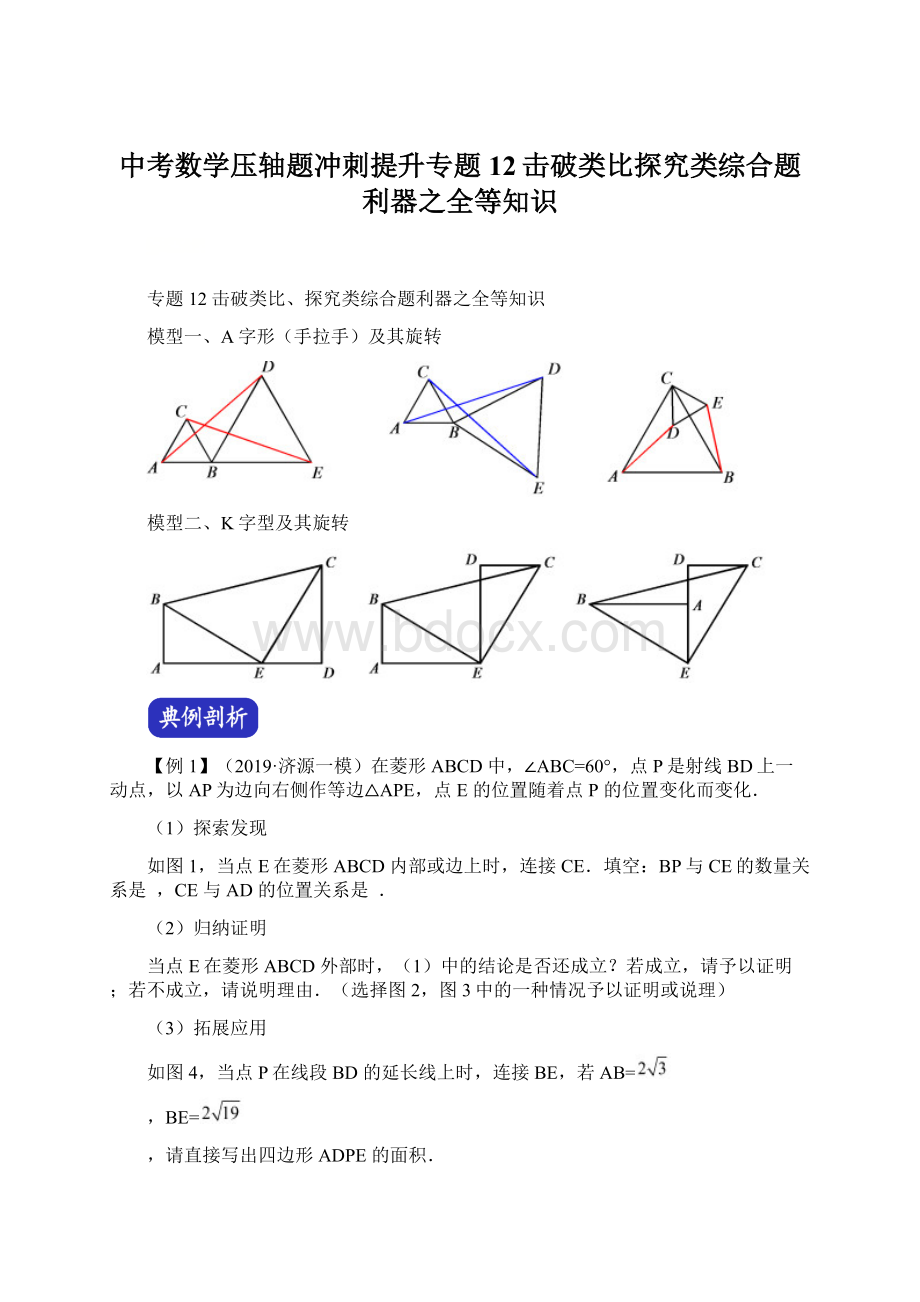
模型一、A字形（手拉手）及其旋转

模型二、K字型及其旋转

【例1】（2019·济源一模）在菱形ABCD中，∠ABC=60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．

（1）探索发现

如图1，当点E在菱形ABCD内部或边上时，连接CE．填空：

BP与CE的数量关系是，CE与AD的位置关系是．

（2）归纳证明

当点E在菱形ABCD外部时，

（1）中的结论是否还成立？

若成立，请予以证明；若不成立，请说明理由．（选择图2，图3中的一种情况予以证明或说理）

（3）拓展应用

如图4，当点P在线段BD的延长线上时，连接BE，若AB=

，BE=

，请直接写出四边形ADPE的面积．

图1图2

图3图4

【答案】

（1）BP=CE，CE⊥AD；

（2）（3）见解析.

【解析】解：

（1）连接AC，延长CE至AD，

∵四边形ABCD是菱形，∠ABC=60°，

∴∠BAD=120°，

∴∠BAC=60°，∠CAD=60°，

∴△ABC是等边三角形，

∴AB=AC，

∵△APE是等边三角形，

∴AP=AE，∠PAE=60°，

∴∠BAP=∠CAE，

∴△BAP≌△CAE，

∴BP=CE，

∵∠ABC=60°，

∴∠ABP=30°，

∵△BAP≌△CAE，

∴∠ABP=∠ACE=30°，

∵∠CAD=60°，

∴∠ACE+∠CAD=90°，

即CD⊥AD.

（2）结论仍然成立，理由如下：

（以图2为例）

连接AC，设CE与AD交于点H，

∵四边形ABCD是菱形，∠ABC=60°，

∴△ABC和△ACD是等边三角形，∠ABD=∠CBD=30°，

∴AB=AC，∠BAC=60°，

∵△APE是等边三角形，

∴AP=AE，∠PAE=60°，

∴∠BAP=∠CAE，

∴△BAP≌△CAE，

∴BP=CE，∠ACE=∠ABP=30°，

∵∠CAH=60°，

∴∠AHC=90°，即CE⊥AD；

（3）连接AC交BD于O，连接CE，

由

（2）知，CE⊥BC，

∵AB=

，BE=

，

在Rt△BCF中，由勾股定理得：

CE=8，

由△BAP≌△CAE，

得：

BP=CE，BD=6，

∴DP=BP－BD=2，

AO=

，

在Rt△AOP中，由勾股定理得：

AP=

，

∴S=S△ADP+S△APE

=

=8

.

【变式1-1】（2019·周口二模）在△ABC中，∠ABC为锐角，点M为射线AB上一动点，连接CM，以点C为直角顶点，以CM为直角边在CM右侧作等腰直角三角形CMN，连接NB．

（1）如图1，图2，若△ABC为等腰直角三角形，

问题初现：

①当点M为线段AB上不与点A重合的一个动点，则线段BN，AM之间的位置关系是_____________，数量关系是______________；

深入探究:

②当点M在线段AB的延长线上时，判断线段BN，AM之间的位置关系和数量关系，并说明理由；

类比拓展:

（2）如图3，∠ACB≠90°，若当点M为线段AB上不与点A重合的一个动点，MP⊥CM交线段BN于点P，且∠CBA=45°，BC=

，当BM=_________时，BP的最大值为__________．

图1图2图3

【答案】

（1）BN⊥AM，BN=AM；

（2）见解析，（3）2，1.

【解析】解：

（1）由AC=BC，∠ACM=∠BCN，CM=CN，可证△ACM≌△BCN，

∴BN=AM，∠A=∠CBN=45°，

∴∠ABN=90°，即BN⊥AM.

（2）BN⊥AM，BN=AM；理由如下：

∵△ABC是等腰直角三角形，∴AC=BC，∠A=∠ABC=45°，∠ACB=90°，

同理，∠NCM=90°，NC=MC,

∴∠ACM=∠BCN，

∴△ACM≌△BCN，

∴BN=AM，∠A=∠CBN=45°，

∴∠ABN=90°，即BN⊥AM.

（3）过C作CG⊥BC交BA的延长线于G，过C作CH⊥AB于H，如图所示，

易证△GCM≌△BCN，

由

（2）知，BN⊥AB，

∴△CHM∽△MBP，

∴

即

设BM=x，

则BP=

，

∴当BM=2时，BP取最小值，最小值为1.

【例2】（2018·洛阳三模）在正方形ABCD中，动点E、F分别从D、C两点出发，以相同的速度在直线DC，CB上移动.

（1）如图1，当点E在边CD上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理由；

（2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，

（1）中的结论还成立吗？

（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：

CD的值；

（3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD=2，试求出线段CP的最大值．

【答案】见解析.

【解析】解：

（1）AE=DF，AE⊥DF，理由如下：

∵四边形ABCD是正方形，

∴AD=DC，∠ADE=∠DCF=90°，

由题意知：

DE=CF，

∴△ADE≌△DCF，

∴AE=DF，∠DAE=∠FDC，

∵∠ADE=90°，

∴∠ADP+∠CDF=90°，

∴∠ADP+∠DAE=90°，

∴∠APD=180°﹣90°=90°，

∴AE⊥DF；

（2）

（1）中的结论还成立，CE：

CD=

或2，

理由如下：

①如图，当AC=CE时，

设正方形ABCD的边长为a，由勾股定理得：

AC=CE=

a，

则CE：

CD=

a：

a=

；

②如图，当AE=AC时，

设正方形ABCD的边长为a，由勾股定理得：

AC=AE=

a，

∵四边形ABCD是正方形，∴∠ADC=

90°，即AD⊥CE，

∴DE=CD=a，

∴CE：

CD=2a：

a=2；

故，CE：

CD=

或2；

（3）∵点P在运动中∠APD=90°，

∴点P的路径是以AD为直径的圆，

如图，设AD的中点为Q，连接CQ并延长交圆Q于点P，此时CP的长度最大，

在Rt△QDC中，由勾股定理得：

QC=

，

∴CP=QC+QP=

+1，

即线段CP的最大值是

+1．

【变式2-1】（2019·西华县一模）如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．

（1）请判断：

FG与CE的数量关系是　　，位置关系是　　；

（2）如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，

（1）中结论是否仍然成立？

请作出判断并给予证明；

（3）如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，

（1）中结论是否仍然成立？

请直接写出你的判断．

图1图2图3

【答案】

（1）FG=CE，FG∥CE；

（2）（3）见解析．

【解析】解：

（1）FG=CE，FG∥CE；

∵BF=CE，BC=CD，∠FBC=∠DCE=90°，

∴△BCF≌△CDE，

∴∠DEC=∠CFB，

∵∠CFB+∠FCB=90°，

∴∠DEC+∠FCB=90°，

即CF⊥DE，

∵DE⊥EG，

∴EG∥CF，

∴EG=DE=CF，

∴四边形FCEG是平行四边形，

∴FG=CE，FG∥CE；

（2）∵BF=CE，BC=CD，∠FBC=∠DCE=90°，

∴△BCF≌△CDE，

∴∠DEC=∠CFB，CF=DE，

∵∠CFB+∠FCB=90°，

∴∠DEC+∠FCB=90°，

即CF⊥DE，

∵DE⊥EG，

∴EG∥CF，

∴EG=DE=CF，

∴四边形FCEG是平行四边形，

∴FG=CE，FG∥CE；

（3）成立．

由上可证：

△CBF≌△DCE，

得：

∠BCF=∠CDE，CF=DE，

∵EG=DE，

∴CF=EG，

∵DE⊥EG

∴∠DEC+∠CEG=90°

∵∠CDE+∠DEC=90°

∴∠CDE=∠CEG，

∴∠BCF=∠CEG，

∴CF∥EG，

∴四边形CEGF平行四边形，

∴FG∥CE，FG=CE．

1.（2019·河南南阳一模）我们定义：

如图1，在△ABC中，把AB绕点A顺时针旋转α（0°<α<180°）得到AB’，把AC绕点A逆时针旋转β得到AC’，连接B’C’，当α+β=180°时，我们称△AB’C’是△ABC的“旋补三角形”，△AB’C’边B’C’上的中线AD是△ABC的旋补中线，点A叫旋补中心.

特例感知：

（1）在图2，图3中，△AB’C’是△ABC的“旋补三角形”，△AB’C’边B’C’上的中线AD是△ABC的旋补中线，

①如图2，当△ABC是等边三角形时，AD与BC的数量关系是

②如图3，当∠BAC=90°，BC=8时，则AD的长为

猜想论证：

（2）如图1，当△ABC是任意三角形时，猜想AD与BC的数量关系，并给予证明.

【分析】

（1）①由△ABC是等边三角形，得AB=BC=AC=AB’=AC’，∠BAC=60°，∠BAC+∠B’AC’=180°，得∠B’=∠C’=30°，即BC=2AD；②可利用“直角三角形中，斜边的中线等于斜边的一半”，证得：

BC=2AD，AD=4；

（2）BC=2AD，利用倍长中线构造全等三角形，延长AD至M使DM=AD，连接B’M，C’M，证得△ABC≌△B’AM，得BC=AM，BC=2AD.

【解析】解：

（1）①∵△ABC是等边三角形，

∴AB=BC=AC=AB’=AC’，∠BAC=60°，

∵DB’=DC’，

∴AD⊥B’C’，

∵BAC+∠B’AC’=180°，

∴∠B’AC’=120°，

∴∠B’=∠C’=30°，

∴BC=2AD，

即：

答案为BC=2AD.

②∵∠BAC=90°，BAC+∠B’AC’=180°，

∴∠B’AC’=∠BAC=90°

∵AB=AB’，AC=AC’，

∴△BAC≌△B’AC’，∴BC=B’C’，

∵B’D=DC’，

∴BC=2AD，

∵BC=8，

∴AD=4；

（2）结论：

BC=2AD，理由如下：

如图，延长长AD至M使DM=AD，连接B’M，C’M，

∵AD=DM，B’D=DC’，

∴四边形AC’MB’是平行四边形，

∴AC’=B’M=AC，

∵∠BAC+∠B’AC’=180°，∠AB’M+∠B’AC’=180°，

∴∠BAC=∠AB’M，

∵AB=AB’，

∴△BAC≌△AB’M，

∴BC=AM，

即BC=2AD.

2.（2019·郑州外国语测试）已知如图1所示，在△ABC中，∠ACB=90°，AC=BC，点D在AB上，DE⊥AB交BC于E，点F是AE的中点，

（1）写出线段FD与线段FC的关系并证明；

（2）如图2所示，将△BDE绕点B逆时针旋转α（0°＜α<90°），其它条件不变，线段FD与线段FC的关系是否变化，写出结论并证明；

（3）将△BDE绕点B逆时针旋转一周，如果BC=4，BE=2

，直接写出线段BF的范围.

【答案】见解析.

【解析】解：

（1）FD=FC，FD⊥FC，理由如下：

由题意知：

∠ADE=∠ACE=90°，AF=EF，

∴DF=AF=EF=CF，

∴∠FAD=∠FDA，∠FAC=∠FCA，

∴∠DFE=∠FDA+∠FAD=2∠FAD，∠EFC=2∠FAC，

∵CA=CB，∠ACB=90°，

∴∠BAC=∠B=45°，

∴∠DFC=∠EFD+∠EFC=2（∠FAD+∠FAC）=90°，

∴FD=FC，FD⊥FC.

（2）结论不变，理由如下：

延长AC至M使得CM=AC，延长ED至N，使DN=DE，连接BN、BM、EM、AN，延长ME交AN于H，交AB于O，如图所示，

∵BC⊥AM，AC=CM，

∴AB=BM，同理得：

BE=BN，

∵∠ABM=∠EBN，∠NBA=∠EBM，

∴△ABN≌△MBE，

∴AN=EM，∠BAN=∠BME，

∵AF=FE，AC=CM，

∴CF=

EM，CF∥EM，

同理，FD=

AN，FD∥AN，

∴FD=FC，

∵∠BME+∠BOM=90°，∠BOM=∠AOH，

∴∠BAN+∠AOH=90°，

∴∠AHO=90°，

即AN⊥MH，

∴FD⊥FC.

（3）由题意知，当点E落在线段AB上时，BF的长最大，如图所示，

此时BF=3

，

当点E落在AB的延长线上时，BF的长最小，如图所示，

此时，BF=

，

∴

≤BF≤3

.

3.（2019·偃师一模）特殊：

（1）如图1，在等腰直角三角形ABC中，∠ACB=90°．作CM平分∠ACB交AB于点M，点D为射线CM上一点，以点C为旋转中心将线段CD逆时针旋转90°得到线段CE，连接DE交射线CB于点F，连接BD，BE．

填空：

①线段BD，BE的数量关系为；②线段BC，DE的位置关系为．

一般：

（2）如图2，在等腰三角形ABC中，∠ACB=α，作CM平分∠ACB交AB于点M，点D为△ABC外部射线CM上一点，以点C为旋转中心将线段CD逆时针旋转α度得到线段CE，连接DE，BD，BE．请判断

（1）中的结论是否成立，请说明理由．

特殊：

（3）如图3，在等边三角形ABC中，作BM平分∠ABC交AC于点M，点D为射线BM上一点，以点B为旋转中心将线段BD逆时针旋转60°得到线段BE，连接DE交射线BA于点F，连接AD，AE．若AB=4，当△ADM与△AFD全等时，请直接写出DE的值．

图1图2图3

【答案】

（1）BD=BE，BC⊥DE；

（2）（3）见解析.

【解析】解：

（1）由题意知：

∠ACM=∠BCM=45°，

由旋转知，∠DCE=90°，CD=CE，

∴∠ECB=∠DCB=45°，

∵BC=BC，

∴△BCD≌△BCE，

∴BD=BE，

∵CD=CE，

∴BC是线段DE的垂直平分线，

∴BC⊥DE，

（2）成立，理由如下，

∵CM平分∠ACB，∠ACB=α，

∴∠ACM=∠BCM=

，

由旋转知，∠DCE=α，CD=CE，

∴∠BCD=∠BCE=

又∵BC=BC，

∴△BCD≌△BCE，

∴BD=BE，

∵CD=CE，

∴BC是线段DE的垂直平分线，

∴BC⊥DE.

（3）①如图3，可证得：

∠ABE=∠ABD=30°，AB⊥DE，

由△ADM≌△ADF，得：

∠FAD=∠MAD=30°，

∴AF=BF=2，

∴DE=2DF，

在Rt△ADF中，DF=AF·tan∠DAF=

，

即DE=

.

②如下图所示，

同理，得∠FBD=30°，AB=AD=4，

∠ADF=∠ADM=30°，

∴DE=2DF=4

，

综上所述，DE的长为：

，4

.

4.（2019·省实验一模）观察猜想

（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；

探究证明

（2）在

（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；

拓展延伸

（3）如图③，在△ABC中，AB＝AC，∠BAC＝a，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝a，连接BF，则BE+BF的值是多少？

请用含有n，a的式子直接写出结论．

图1图2图3

【答案】

（1）BF⊥BE；BC；

（2）（3）见解析.

【解析】解：

（1）∵∠EAF＝∠BAC＝90°，

∴∠EAF－∠BAE＝∠BAC－∠BAE,

∴∠BAF＝∠CAE，

∵AF＝AE，AB＝AC，

∴△BAF≌△CAE，

∴∠ABF＝∠C，BF＝CE，

∵AB＝AC，∠BAC＝90°，

∴∠ABC＝∠C＝45°，

∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，

故答案为:

BF⊥BE，BC．

（2）过D作DH∥AC交BC于H，

∵DH∥AC，

∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，

由

（1）可证得：

BF⊥BE，BF+BE＝BH，

∵AB＝AC＝3，AD＝1，

∴BD＝DH＝2，

∴BH＝2

，

∴BF+BE＝BH＝2

；

（3）过D作DH∥AC交BC的延长线于H，作DM⊥BC于M．

∵AC∥DH，

∴∠ACH＝∠H，∠BDH＝∠BAC＝α，

∵AB＝AC，

∴∠ABC＝∠ACB

∴∠DBH＝∠H，

∴DB＝DH，

∵∠EDF＝∠BDH＝α，

∴∠BDF＝∠HDE，

∵DF＝DE，DB＝DH，

∴△BDF≌△HDE，

∴BF＝EH，

∴BF+BE＝EH+BE＝BH，

∵DB＝DH，DM⊥BH，

∴BM＝MH，∠BDM＝∠HDM，

∴BM＝MH＝BD•sin

．

∴BF+BE＝BH＝2n•sin

．

5.（2019·濮阳二模）在△ABC中，AC＝BC，∠ACB＝α，点D为直线BC上一动点，过点D作DF∥AC交AB于点F，将AD绕点D顺时针旋转α得到ED，连接BE．

（1）特例猜想

如图1，当α＝90°时，试猜想：

①AF与BE的数量关系是；②∠ABE＝；

（2）拓展探究

如图

（2），当0°＜α＜90°时，请判断AF与BE的数量关系及∠ABE的度数，并说明理由．

（3）解决问题

如图（3），在△ABC中，AC＝BC，AB＝8，∠ACB＝α，点D在射线BC上，将AD绕点D顺时针旋转α得到ED，连接BE，当BD＝3CD时，请直接写出BE的长度．

图1图2图3

【答案】

（1）AF＝BF，90°；

（2）（3）见解析.

【解析】解：

（1）设AB交DE于O．

∵∠ACB＝90°，AC＝BC，

∴∠ABC＝45°，

∵DF∥AC，

∴∠FDB＝∠C＝90°，

∴∠DFB＝∠DBF＝45°，

∴DF＝DB，

∵∠ADE＝∠FDB＝90°，

∴∠ADF＝∠EDB，

∵DA＝DE，

∴△ADF≌△EDB，

∴AF＝BE，

∴∠DAF＝∠E，

∵∠AOD＝∠EOB，

∴∠ABE＝∠ADO＝90°，

所以答案为AF＝BF，90°．

（2）结论：

AF＝BE，∠ABE＝α．理由如下：

∵DF‖AC

∴∠ACB＝∠FDB＝α，∠CAB＝∠DFB，

∵AC＝BC，

∴∠ABC＝∠CAB，

∴∠ABC＝∠DFB，

∴DB＝DF，

∵∠ADF＝∠ADE﹣∠FDE，∠EDB＝∠FDB﹣∠FDE，

即∠ADF＝∠EDB，

∵AD＝DE，

∴△ADF≌△EDB，

∴AF＝BE，∠AFD＝∠EBD

∵∠AFD＝∠ABC+∠FDB，∠DBE＝∠ABD+∠ABE，

∴∠ABE＝∠FDB＝α．

（3）分两种情况讨论：

①当点D在线段BC上时，

由

（2）可知：

BE＝AF，

∵DF∥AC，

∴

，

∵AB＝8，

∴AF＝2，

∴BE＝AF＝2，

②当点D在BC的延长线上时，

∵AC∥DF，

∴

，

∵AB＝8，

∴AF＝4，即BE=4，

综上所述，BE的长度为2或4．

6.（2019·开封二模）问题发现

如图1，△ABC是等边三角形，点D是边AD上的一点，过点D作DE∥AC交AC于E，则线段BD与CE有何数量关系？

拓展探究

如图2，将△ADE绕点A逆时针旋转角α（0°＜α＜360°），上面的结论是否仍然成立？

如果成立，请就图中给出的情况加以证明．

问题解决

如果△ABC的边长等于2

，AD＝2，直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长．

图1图2备用图

【答案】见解析．

【解析】解：

（1）如图1，BD＝CE，理由是：

∵△ABC是等边三角形，

∴AB＝AC，

∵DE∥BC，

∴△ADE是等边三角形，即AD=AE，

∴BD＝CE；

（2）结论仍然成立，

由图1得：

AD＝AE，

由旋转性质得：

∠BAD＝∠CAE，

∵AB=AC，

∴△BAD≌△CAE，

∴BD＝CE；

（3）分两种情况讨论，

①如图所示，过D作DG⊥AB，垂足为G，

∵AF⊥DE，AD=AE，

∴∠DAF＝∠EAF＝30°，

∴∠BAD＝30°，

由AD＝2，得：

DG＝1，AG＝

，

由AB＝2

，得：

BG＝

，

由勾股定理得：

BD＝2．

②如图，

由

（2）中证明可知：

△BAD≌△CAE，

∴BD＝CE，

∵AD＝AE，DE⊥AC，∠ADE＝60°

∴∠EAF＝∠FAD＝30°，

∴EF＝FD＝

AD＝1，

∴AF＝

，

∴CF＝AC+CF＝3

，

在Rt△EFC中，由勾股定理得：

EC＝2

，

∴BD＝EC＝2

，

综上所述，BD的长为2或2

．

7.（2019·安阳二模）

（1）问题发现：

如图1，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，则AB，AD，DC之间的数量关系为　　．

（2）问题探究：

如图2，在四边形ABCD中，AB∥DC，E是BC的中点，点F是DC的延长线上一点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的数量关系，并证明你的结论

（3）问题解决：

如图3，AB∥CD，点E在线段BC上，且BE：

EC＝3：

4．点F在线段AE上，且∠EFD＝∠EAB，直接写出AB，DF，CD之间的数量关系．

图1图2图3

【答案】

（1）AD＝AB+CD；

（2）（3）见解析．

【解析】解：

（1）结论：

AD＝AB+CD．

理由：

∵AB∥CF，

∴∠CFE＝∠EAB，

∵CE＝EB，∠CEF＝∠AEB，

∴△CEF≌△BEA，

∴AB＝CF．

∵AF平分∠DAB，

∴∠DAF＝∠EAB，

∵∠EAB＝∠CFE，

∴∠DAF＝∠DFA，

∴AD＝DF，

∵DF＝DC+CF＝CD+AB，

∴AD＝AB+CD．

（2）结论：

AB＝AF+CF．

理由：

延长AE、DC交于G，

∵AB∥DG，

∴∠G＝∠EAB，

∵CE＝EB，∠CEG＝∠BEA，

∴△CEG≌△BEA，

∴AB＝CG，∠G＝∠EAB，

∵AE平分∠FAB，

∴∠FAG＝∠EAB，

∵∠G＝∠EAB，

∴∠FAG＝∠G，

∴FA＝FG，

∵CG＝CF+FG＝CF+AF，

∴AB＝AF+CF．

（3）结论：

AB＝

（CD+DF）．

延长AE、CD交于G．

∵CG∥AB，

∴

，∠G＝∠A，

∴AB＝

CG，

∵∠DFE＝∠A，

∴∠DFG＝∠G，

∴DF＝DG，

∴CD+DF＝CD+DG＝CG，

∴AB＝

（CD+DF）．

8.（2019·中原名校大联考）如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接D