弦图之妙.docx
《弦图之妙.docx》由会员分享,可在线阅读,更多相关《弦图之妙.docx(22页珍藏版)》请在冰豆网上搜索。
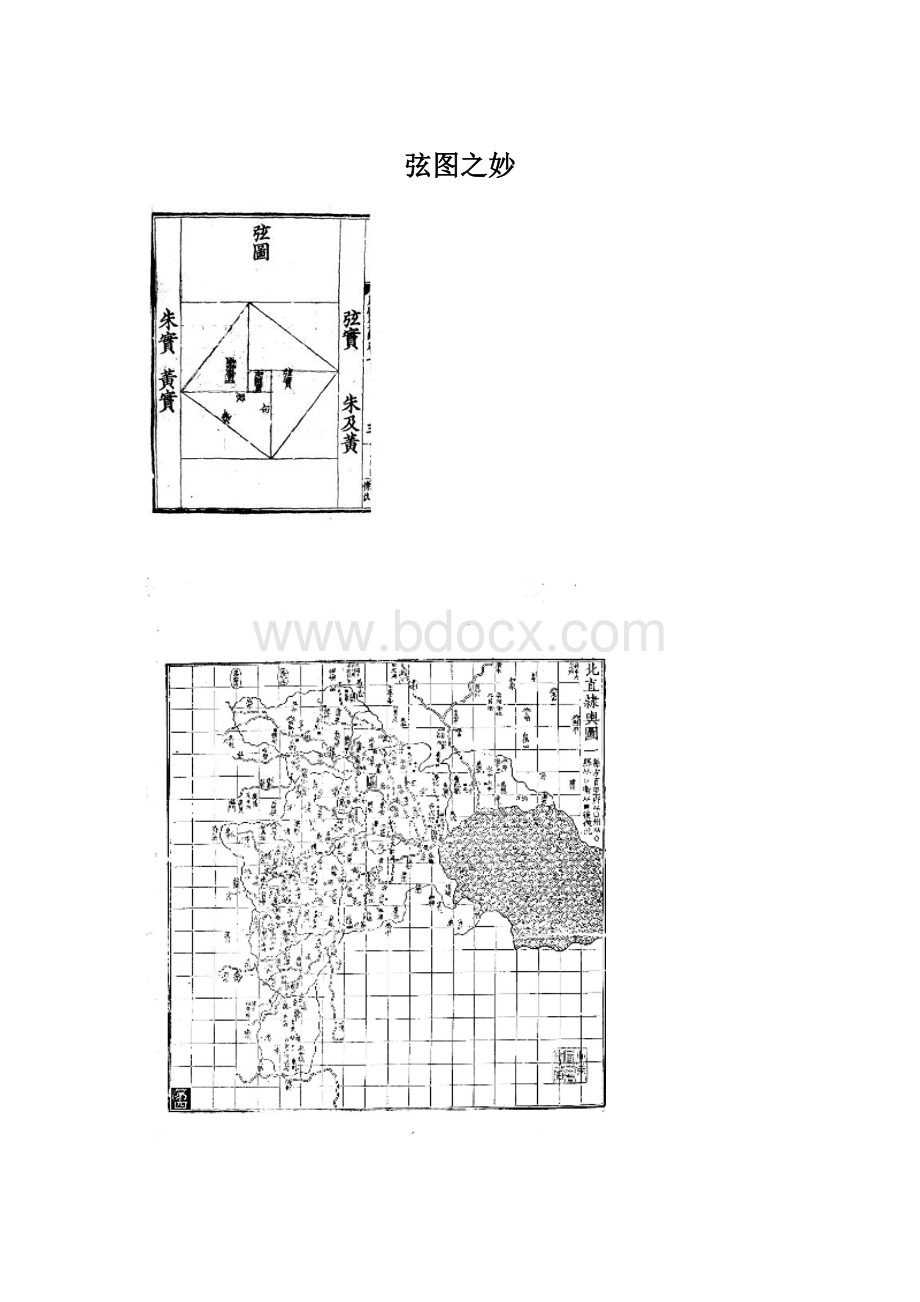
弦图之妙
《周髀算经》∶把勾股定律当常识的天文书
给你一根八尺长的棍子,和一个“勾三股四弦五”的提示,请问你“地球距离太阳有多远?
”
这个题目你能答得出来吗?
这个题目就是出现在近二千年前的《周髀算经》上。
古人不会电脑,但是也不见得就是没有科学能力,他们对二十四节气、二十八星宿……都有很深的认识了。
除了前述“以日影求日高”的题目外,还有一题是用“璇玑”(即北斗星的第一颗到第四颗星,状如“口”字少掉一笔的“ㄈ”)来量测太阳直径,也是出现在同一本《周髀算经》。
这个题目你也答得出来吗?
《周髀算经》简称《周髀》,其中的“周”指的是周代,而“髀”(读bì)的原意是大腿或大腿骨,此处意思是“表(竿)”,是一种“用来测量日影长度的表(状如长棍)”全书以周公和商子的对谈开场。
从“勾三股四弦五”谈起,从日影、日高、不同纬度的日高、不同节气的日高……,到一年中24个节气各时节的日影表;表面谈的是天文,但是行文中也出现开方、等差级数的数学概念了。
它出版的年代最迟不晚过汉代。
《周髀算经》除了有后汉赵君卿的注释外,唐代的李淳风、宋代的李籍等多人也都有注释过。
在唐代,《周髀算经》还被选列为《算经十书》之一,是科举取士中“明算科”应试者要研读的算学教科书之一。
《周髀算经》全书分为上、下二卷,体裁格式从对谈式(周公、商高,陈子、荣方),到独白式(法曰、术曰)作为不同单元的开头。
英国人李约瑟(JosephT.M.Needham,1900~1995)博士把此书按西人习用的格式来分章节∶
第一章是周公与商高对谈∶第一节谈商高定律、第二节谈表竿、方、圆的使用与距离的量测;
第二章是荣方与陈子的对谈∶第一节继续谈日影的变化,乃至以璇玑太阳直径;第二节以日高图开始;第三节以七衡图开始。
第三章各节才是原书的各章∶谈论范围从太阳的岁动、各节气的日影长度,到各恒星、二十八宿、十九年周期……。
对于举头不识星斗、低头不熟文言文的现代人,还真的像是一本“天书”呢。
《周髀算经》书中最有名的一句话除了“径一周三”(圆周率),要算是“勾三股四弦五”了,稍后还有一句“句股各自乘并而开方除之”,简直就是把a2+b2=c2和c2开平方的算法,都当成国民常识,随口带过,反而让后代子孙大叹它比古希腊的“毕氏定律”还要早出现,所以课本上的“毕氏定律”都应该改称为“勾股定律”或“商高定律”。
其实,单看赵爽注释的“句股圆方图”(即上图之弦图),把“勾三股四弦五”的“常识”,用面积重组的方式,简洁地给证明出来。
就令人赞叹不已。
可惜许多现代人,还以为中国古人那些线装书都是很落伍的。
本文来自神州智慧网()
详文参考:
2002年世界数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。
中算史中的『張本例』(genericexamples)
台師大數學系洪萬生教授
最近與研究生一起研讀MaciaPinto,DavidTall的“BuildingFormalMathematicsonVisualImagery:
Acasestudyandatheory”(2002)與JohnMasonandDavidPimm的“GenericExamples:
Seeingthegeneralintheparticular”(1984)兩篇論文,發現其中有一些論述可以關連到HPM上頭來。
事實上,中算史文本中也有很多『張本例』(genericexamples),可供HPM研究者或使用者參考與援用。
茲在此列舉一二,聊供談助可也。
何謂『張本例』?
或許我們可以看看如何利用它來證明!
如果有人利用下列圖示來『證明』:
偶數加偶數等於偶數,那麼,我們就可以說他(她)使用了『張本例』:
●●●加●●●●等於●●●●●●●
●●●●●●●●●●●●●●
根據英文字典的說明,“generic’是“genus”(『類』或『屬』)的形容詞,意思是某『類』(class)或『群體』(group)所共有的(特性)。
這樣說來,如果不夠明白,我們不妨『訴諸』權威。
上述Mason與Pimm兩人合寫的論文中,曾引述了希爾伯特(DavidHilbert)的一段『夫子自道』,非常值得在此引述:
假使你想要解題,首先,剝除與此一問題本質(essential)無關的任何事物。
簡化此一問題,並且盡可能地在不犧牲它的核心(core)的情況下將它特殊化(specialize)。
如此一來,它會變得簡單(simple),盡可能簡單,但卻不會喪失它的任何『精華』(punch),然後,你就可以來解題了。
至於所謂的延拓(generalization),不過是一種你毋需太過勞神的無聊之舉(triviality)。
在這一段中譯引文中,我刻意地附上原文中(的英文)如essential,core,specialize,simple,generalization,triviality等等二十世紀數學家修辭用的口頭禪,忠實地保留一點『原味』,希望大家喜歡!
不過,Mason與Pimm引述的主要目的是指出:
希爾伯特的『進路』(approach)可以說是在於尋找一個『張本例』,它儘管特殊(specialization)但卻談論了一般(generality)。
因此,他們才會在上述論文中的副標題中,強調從特殊性中看到一般性(Seeingthegeneralityintheparticular)。
換句話說,對他們來說,「張本例固然是一個真實的例子,但是它卻以被刻意要求成為『承載一般性』的角色來呈現(Agenericexampleisanactualexample,butonepresentedinsuchawayastobringoutitsintendedroleasthecarrierofthegeneral)。
」
現在,我們就舉中算史上的兩個『張本例』,來說明它們在證明上可以發揮的積極功能。
第一例出自三國時代孫吳國的趙爽,他對勾股定理提供了一個非常漂亮的『弦圖』證明,請參考下圖,其中根據三、四、五這三個特殊的數目所作的圖形,就很容易『搖身一變』,而成為勾、股、弦分別是a,b,c的『弦圖』,因此,我們從趙爽的弦圖『特殊性』,很容易看出它的『一般性』來。
另一個例子,則出自南北朝時代的《孫子算經》。
在本書的下卷中有一個『物不知數』題,堪稱是『中國剩餘定理』(ChineseRemainderTheorem)的起點,茲引述內容如下:
今有物,不知其數,三、三數之賸二,五、五數之賸三,七、七數之賸二,問物幾何?
答曰:
二十三。
術曰:
三、三數之賸二,置一百四十;五、五數之賸三,置六十三;七、七數之賸二,置三十。
併之,得二百二十三,以二百一十減之,即得。
凡三、三數之賸一,則置七十;五、五數之賸一,則置二十一;七、七數之賸一,則置十五。
一百六以上,以一百五減之,即得。
在本題中,如果我們利用任意三個兩兩互質的除數替代三、五、七,而且餘數也改成任意不相等的三個整數(但分別小於前述的三個除數),那麼,在『術曰』中的『一百四十』、『六十三』、『三十』、『七十』、『二十一』、『十五』等數,也就可以跟著『改寫』成為對應的數,從而得證(一般性)的『中國剩餘定理』了。
最後,有關『張本例』一詞的敲定,我們必須作一點說明。
它也被稱為『啟蒙例』或『構念例』。
然而,我們若將“genericexample”中譯成『張本例』,或許更加貼切傳神,蓋取其『彰顯本質屬性』之義也!
我的考慮是基於下列對比:
genusvs.species,genericvs.special,generalityvs.specialization,請大家批評與指教。
弦图之妙赏弦图之美 用弦图之妙
河南 王兵伟
早在一千三百多年前,我国著名的数学家赵爽巧妙的借助面积,证明了勾股定理,下图就是赵爽证题时用到的图形,史称“弦图”;此图不仅构造巧妙美观,而且还蕴含着不少“玄机”;
一、引出结论:
由于△AFE、△EFR、△EBH、△EHQ、△HCG、△HGP、△GDF、△FGO都是全等的Rt△,设它们的面积为S,则
=4S+
,
=8S+
,于是不难得出如下结论:
……①;我们不妨在此弦图—正方形的基础上推广延伸到矩形中去,如下图:
易知
……②,利用此结论可以轻松的求解与
此相关的问题;
二、应用举例:
例1、如右图,在一个由4×4个小正方形组成的正方
形网格中,阴影部分面积与正方形ABCD的面积比
是( )
A.3:
4 B.5:
8 C.9:
16 D.1:
2
解析:
此题图形可构造成下图所示的“弦图”:
设小正方形的边长为a,由结论①
得:
所以阴影部分面积与正方形ABCD的面积比是:
,故选D;
例2、如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则矩形ABCD的面积为( )
A、2 B、
C、
D、
解析:
设小正方形的边长为a,则矩形ABCD的面积为15a2,由结论②
得:
,
所以
,矩形ABCD的面积为
,故选D;
例3、如下图,正方形ABCD的面积是S,A、B、C、D分别是线段EB、FA、GD、HC的三等分点,试用S表示四边形EFGH的面积S1;
解析:
构造如上图所示的“弦图”,设正方形ABCD的边长是2a,则正方形OPQR的边长是3a,由结论①
得:
因为正方形ABCD的面积S=
,所以四边形EFGH的面积S1=
S.
【本讲教育信息】
一.教学内容:
用“弦图”求面积
同学们,你们好!
今天,我们一起来研究“弦图”的知识。
这就是一个“弦图”。
“弦”图是由八个完全一样的直角三角形拼成四个相同的长方形围成的,中间空出一个小正方形。
三国时期的吴国数学家赵爽,就利用这“弦图”对勾股定理作出了严格而简捷的证明。
我们也可以根据“弦图”中大小正方形与长方形的关系,得到一些面积问题的解题思路。
(一)阅读思考
例1.有一大一小的两个正方形(如下图),对应边之间的距离都是1厘米,如果夹在两个正方形之间部分的面积为12平方厘米,那么大正方形的面积是多少?
分析与解答:
要想求出图中大正方形的面积,根据公式,只要先求出大正方形或小正方形的边长就行。
下面我们就设法求出这两个量中的某个量。
解这道题有很多种方法;但都要添加辅助线。
方法1:
方法2:
方法3:
方法4:
图中两个梯形共12平方厘米,它们每个面积是
平方厘米,因为梯形的高是2厘米,所以梯形上下底之和是
厘米,上下底之差是2厘米,所以梯形的上底(大正方形边长)是4厘米,所以大正方形面积是
平方厘米。
例2.从一个正方形的木板上锯下宽0.5米的一个长方形木条以后,剩下的长方形的面积为5平方米,问锯下的长方形木条的面积等于多少?
分析与解答:
我们可以将四个剩下的长方形这样的木板拼成一个如下图的“弦图”。
从图中可以看出,中间的小正方形面积是
平方米,大正方形的面积是
平方米。
由于
,所以大正方形的边长是4.5米。
也就是剩下的长方形的长和宽的和是4.5米,长与宽的差是0.5米。
从图中也可以看出,大正方形的边长=小正方形边长+长方形宽×2,所以长方形的宽是2米,那么长是2.5米。
所以锯下的木条的面积是
平方米。
(二)尝试体验
1.四个完全一样的长方形木板,拼成如图的正方形,大正方形周长32厘米,小正方形周长8厘米。
求:
每块长方形木板的面积和周长。
2.同样大小的长方形纸片摆成下面这样的图形。
已知每张小纸片的宽是12厘米,求阴影部分的总面积。
3.四个相同的小长方形,宽是1厘米,它们的面积和是12平方厘米,求正方形ABCD的面积。
4.有9张相同的小长方形卡片,摆成一个大长方形,已知每个小长方形的周长是18厘米,宽是4厘米,求大长方形的面积。
5.从一块正方形玻璃上裁下宽为16分米的一长方形条后,剩下的那块长方形的面积为336平方分米,原来正方形的面积是多少平方分米?
6.计划修一个正方形的花坛,并在花坛周围铺上宽2米的草坪,草坪的面积是40平方米,那么修建花坛需占地多少平方米?
【模拟试题】(答题时间:
40分钟)
1、有一条红色的正方形丝巾,它的边长是30厘米,丝巾上横竖各有两道宽均为5厘米的黑条,如图中的阴影部分,则丝巾黑色部分的面积是__________平方厘米。
2、四个一样的长方形和一个小正方形拼成一个大正方形,如图,已知大、小正方形的面积分别为81和25平方厘米,则长方形的长是___________厘米,宽是__________厘米。
3、如图,用同样大小的长方形纸片拼成一个大长方形,已知,每张小纸片的宽是8厘米,则阴影部分的面积的和是_________平方厘米。
4、一个斜边是40厘米的直角三角形,两条直角边之差是6厘米,则这个直角三角形的面积是__________平方厘米。
5、用同样的长方形条砖,在一丛花的周围镶成一个正方形边框,如图,边框的外周长为288厘米,里面的小正方形面积为1600平方厘米,则每块长方形砖的长是_________厘米,宽是___________厘米。
6、计划修一个正方形的花坛,并在花坛的周围铺上宽4米的甬道,甬道的面积是80平方米,那么修建花坛(包括甬道)需占地___________平方米。
7、如图,小长方形的长是宽的2倍,两个长方形对应边的距离是1厘米,夹在大、小两个长方形之间的面积是64平方厘米,则小长方形的面积是__________平方厘米。
8、26个长为6厘米的小纸片,摆成如图所示的图形,则阴影部分的面积和是________平方厘米。
【试题答案】
1、答案:
500
解析:
丝巾黑色部分的面积为
(平方厘米)。
2、答案:
7,2
解析:
由已知得,大正方形的边长为9厘米,小正方形的边长为5厘米,又因为长方形的长加宽等于大正方形边长,长减去宽等于小正方形边长,
所以长方形的长为(9+5)÷2=7(厘米),宽为(9-5)÷2=2(厘米)。
3、答案:
48
解析:
由原图可知,5个小长方形的长等于3个小长方形的长加3个宽,所以2个小长方形的长等于3个长方形的宽,则小长方形的长为
(厘米),
每个小阴影部分的边长为12-8=4(厘米),
所以阴影部分面积的和为4×4×3=48(平方厘米)。
4、答案:
391
解析:
用四个这样的直角三角形拼成如图所示的大正方形。
大正方形的面积为
(平方厘米),
小正方形的面积为6×6=36(平方厘米),
一个直角三角形的面积为(1600-36)÷4=391(平方厘米)。
5、答案:
28,16
解析:
由原图可知长方形砖的2个长加上1个宽为288÷4=72(厘米),由已知得,小正方形的边长为40厘米,即长方形砖的2个长减去1个宽为40厘米,所以长方形砖的长为
(厘米),宽为
(厘米)。
6、答案:
81
解析:
如图,小长方形的面积为80÷4=20(平方米),小长方形的长为20÷4=5(米),大正方形的边长为4+5=9(米),所以修建花坛需占地为9×9=81(平方米)。
7、答案:
200
解析:
如图,长方形A的面积为(64-1×4)÷6=10(平方厘米),长方形A的长为10÷1=10(厘米),所以小长方形的面积为(10×2)×10=200(平方厘米)。
8、答案:
8
解析:
由原图可知,3个小纸片的宽等于它的长,所以小纸片宽为6÷3=2(厘米),每个小阴影部分的边长为小纸片的宽,所以阴影部分的面积和为2×2×2=8(平方厘米)。
圖說一體、不證自明
台師大數學系洪萬生教授
本刊曾多次刊出「看圖說話」,贏得不少的注意與好評。
今年十月二十三日,我應邀到台北市西松高中演講(由西松高中教師會舉辦)時,順便介紹了幾張「看圖說話」,沒想到與會的台北市、縣數學教師,竟然立即發現了它們的「力」與「美」,真是令人高興。
最近黃哲男老師在北市建中教學實習,曾利用圖形來講解平方項的求和公式(參見圖一),學生的反應是:
『從小到大第一次感受到數學的美與神奇。
』
那些圖形大部分都從「美國數學協會」(TheMathematicalAssociationofAmerica,簡稱MAA)所出版的MathematicsMagazine所摘錄出來的。
MAA與AMS、NCTM並列為美國三大數學社團,它們關心數學教育的方式,則側重面大有不同。
譬如說吧,AMS即「美國數學學會」(AmericanMathematicalSociety)的簡稱,它的組成份子都是專業數學家,因此,學會出版品中的AmericanMathematicalMonthly與NoticesoftheAmericanMathematicalSociety,雖然不乏教育方面的論述,但是,前者偏向大學層次的解題活動,後者則提供論壇,讓數學家抒發他們對數學教育的熱情關懷與高韜理想。
另一方面,NCTM則處在另一個極端,它是「全國數學教師協會」(NationalCouncilofTeachersofMathematics)的簡稱,出版品中有針對中小學數學教師為訴求對象的TheMathematicsTeacher與TheArithmeticTeacher,內容主要涉及具體的教學策略與方法,可見NCTM是數學教育專家(mathematicseducator)與中小學數學教師的自主團體。
至於MAA則在體制上比較符合中庸之道。
譬如,它的組成份子就容納了專業數學家、大學與中、小學數學教師等各個層面,尤其難得的是,像GeorgePolya這樣的偉大數學家,就曾經是MAA的忠誠會員。
再者,MAA的刊物MathematicsMagazine雖然內容稍偏大學數學層次,但是,教育與人文關懷相當濃厚,所以,它比起AmericanMathematicalMonthly來,顯得「世俗」(secular)一些,然而,就觸及數學知識活動來說,它相較於TheMathematicsTeacher與TheArithmeticTeacher,則無疑「深刻」(deep)多了。
正因為如此,所以,MathematicsMagazine於1975年提出此一「看圖說話」專欄構想,原先只是用以「補白」(useasend-of-articlefillers),沒想到後來主編J.ArthurSeebach與LynnArthurSteen竟然進一步強調:
利用一個令人歡喜的圖示,來提出一個重要的數學觀點,這比起原先目的,恐怕再也不能更好的吧?
顯然由於此一專欄的大受歡迎,因此,MAA的另一份刊物TheCollegeMathematicsJournal在八十年代的稿約中,就不斷地聲明:
本刊除了歡迎側重解釋性的論文之外,「也邀請其他類型的撰稿,尤其是不用文字的證明(Proofswithoutwords)(Proofswithoutwords),數學詩篇,遺聞軼事引述,......」
不過,誠如ProofsWithoutWords:
ExercisesinVisualThinking(MAA出版,1993)的編者RogerB.Nelsen所指出,這種「看圖說話」卻早已不乏先例。
事實上,MartinGardner就曾在1973年十月號的【科學的美國人】(ScientificAmerican)討論這種「不用文字的證明」。
他將這種圖形視為「一瞥就懂」的圖形("look-see"diagrams),這是因為在很多時候一個蠢笨的證明,若能輔以一個幾何的類比圖形(geometricanalogue),則後者的簡潔與美妙,讓讀者幾乎可以一瞥即對定理的真實性瞭然於胸(thetruthofatheoremisalmostseenataglance)。
此外,Nelsen還特別指出:
在數學史上,這種圖形也常常出現。
誠然,中國趙爽、劉徽(三世紀)與印度巴斯卡拉(十一世紀)對畢氏定理所提供的「弦圖證明」(圖二)
,就是十分著名的例子。
可見,它們也曾經在數學史上扮演相當有意義的角色。
針對此一例子,古典希臘的歐幾里得所提供的證法之附圖(圖三),
大概就少了一目瞭然的特性。
究其原因,圖形只被他們認為具有輔助思考的功能而已。
對歐幾里得影響深遠的柏拉圖,在他的【理想國】(TheRepublic)中甚至強調吾人在心靈(mind)思考數學客體(即形式(forms)或理念(ideas))時,千萬不可被圖形所迷惑或左右。
在這種情況下,圖形作為認識或核證數學知識的一種憑藉,希臘數學家對它的『正當性』一定相當保留,於是,他們對文字論述的方式,當然更加全力以赴了。
在數學史上,數學家言說或論述方式總是受限於符號的使用--當然,這也常常關聯到他(她)們對於某些關鍵概念的透明清晰度之掌握,因此,利用圖形的「自我解說」(self-explanation)能力,往往是他(她)們呈現數學知識的一個重要策略。
譬如說吧,十四世紀巴黎學派的Oresme就使用了下列圖四,發現/證明了下列級數和:
至於他所根據的理由則是:
『一個有限面積的平面區域,可以照我們所喜歡的程度去拉長或變高它的延展性,而不改變它的尺寸大小。
』可見,無窮級數如何求和對他來說,數學符號與術語大概都不足以『講明白,說清楚』,因此,想辦法去建構一個圖示,或許是最具說服力了。
所以,偶而在課堂上利用這種圖形,應該可以帶來意想不到的學習結果,至少我們可以利用這種難得的機會,拉近學生與古代數學文本的距離。
尤其,當代數符號演算對初學者極為抽象時,幾何圖示(geometricdemonstration/illustration)往往可以發揮相當大的澄清或說服功能,譬如【幾何原本】中的平方和公式之圖示(圖五),
以及阿爾花拉子摩(Al-Khwarizmi)利用配方法(completingthesquare)來圖示二次方程
(圖六),
都是非常值得參考借鏡的文本,值得我們珍視與利用。
附註:
阿爾花拉子摩的原題敘述成『平方加上10根等於39,問平方是多少?
』,至於解法則寫成:
『取根的係數10的一半,即5,自乘得25,加上39等於64,其平方根是8,在減去根的係數10之半,餘3。
這就是根,它的平方根是9。
』