DCT变换的原理及算法.docx

DCT变换的原理及算法.docx

《DCT变换的原理及算法.docx》由会员分享，可在线阅读，更多相关《DCT变换的原理及算法.docx（27页珍藏版）》请在冰豆网上搜索。

DCT变换的原理及算法

DCT变换的原理及算法

离散傅立叶变换（DiscreteFourierTransform）

离散傅立叶变换概述

傅立叶分析以法国数学家和物理学家JeanBaptisteJosephFourier命名，是一种将信号分解为谐波的方法。

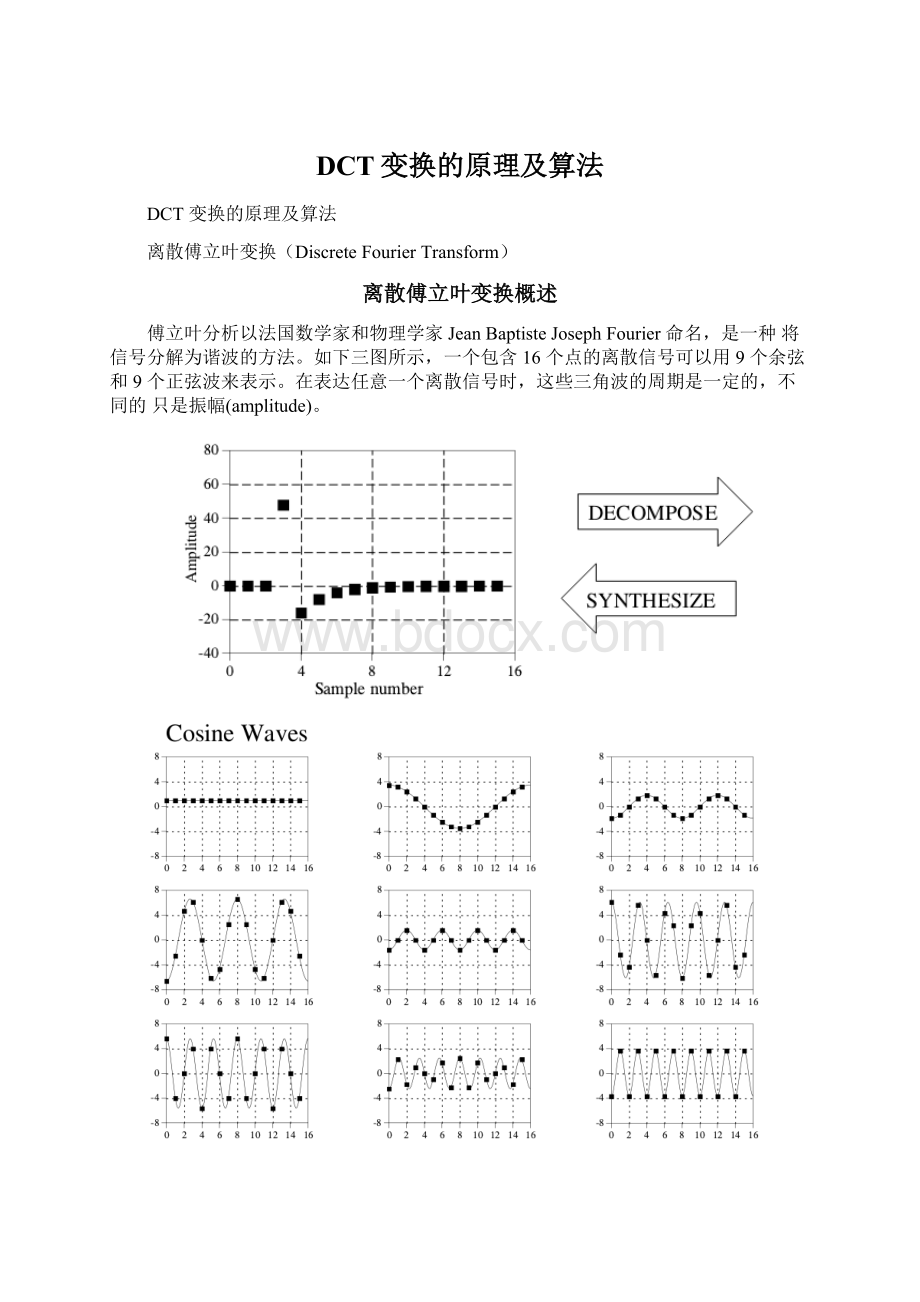
如下三图所示，一个包含16个点的离散信号可以用9个余弦和9个正弦波来表示。

在表达任意一个离散信号时，这些三角波的周期是一定的，不同的只是振幅（amplitude）。

图1-1离散信号与对应的三角波

信号可以是连续的或离散的，同时也可以是周期性的或非周期性的，根据信号的这两个特点，傅立叶变换可以分为四种类型：

傅立叶变换（FourierTransform），处理非周期性的连续信号（Aperiodic-

Continuous）。

傅立叶序列（FourierSeries），处理周期性的连续信号（Periodic-

Continuous）。

离散时间域傅立叶变换（DiscreteTimeFourierTransform），处理非周期性的离散信号（Aperiodic-Discrete）。

离散傅立叶变换（DiscreteFourierTransform），处理周期性的离散信号

（Periodic-Discrete）。

计算机只能处理离散的和有限长度的信号，因此只有离散傅立叶变换（DFT）能在计算

机中以算法实现。

图1-2四种不同类型的傅立叶分析

实数离散傅立叶变换（RealDFT）的格式和表示

如图1-3所示，离散傅立叶变换将包含N个点的输入波转为两个包含N/2+1个点的输出波。

输入波常被称作时间域，因为信号的波形基本上都是随时间变化，输出波常被称作频率域。

时间域与频率域中存储的信息是一样的，只是表现方式不一样。

将时间域转为频率域的过程叫离散傅立叶变换（DFT），将频率域转换为时间域的过程叫反变换（IDFT）。

频率域可以分为两部分，实数部分ReX[]和虚数部分ImX[]，分别存放余弦函数（Cosine）的振幅和正弦函数（Sine）的振幅。

图1-3实数傅立叶变换示意图

DFT基函数

DFT中使用的正弦和余弦函数统称为基函数（BasisFunction），这些三角函数的周

期是固定的，变化的只是振幅。

DFT基函数的表达式：

Ck[i]=cos（2πki/N）

Sk[i]=sin（2πki/N）

公式1-1

其中，Ck[i]和Sk[i]表示由N个点组成的离散正弦曲线，i的取值范围是张倒N-1。

k

决定了曲线的周期，取值范围是0到N/2。

多余的系数

完成DFT后，系数由原来的N个变为N+2个，似乎产生了两个多余的系数。

在频率域中，的确有两个系数是多余的，它们是ImX[0]和ImX[n/2]。

它们的存在使得频率域中的其他系数相互独立，并且它们的值永远为0，因此不会影响反变换。

反变换的计算（IDFT）

公式1-2

在上面的公式中，振幅使用的是

和

，而不是ImX[k]和ReX[k]。

两者的关系可以用下面的公式来表示：

公式1-3

反变换的算法实现

下面是反变换算法的伪代码实现：

100'THEINVERSEDISCRETEFOURIERTRANSFORM

110'Thetimedomainsignal,heldinXX[],iscalculatedfromthefrequencydomainsignals,

120'heldinREX[]andIMX[].130'

140DIMXX[511]'XX[]holdsthetimedomainsignal

150DIMREX[256]'REX[]holdstherealpartofthefrequencydomain160DIMIMX[256]'IMX[]holdstheimaginarypartofthefrequency

domain

170'

180PI=3.14159265'Settheconstant,PI

190N%=512'N%isthenumberofpointsinXX[]200'

210GOSUBXXXX'MythicalsubroutinetoloaddataintoREX[]and

IMX[]

220'

230

240'

'FindthecosineandsinewaveamplitudesusingEq.1-3250FORK%=0TO256

260REX[K%]=REX[K%]/（N%/2）

270IMX[K%]=-IMX[K%]/（N%/2）

280NEXTK%

290'

300REX[0]=REX[0]/2

310REX[256]=REX[256]/2

320'

330'

340FORI%=0TO511

'ZeroXX[]soitcanbeusedasanaccumulator350XX[I%]=0

360NEXTI%

370'

380'Eq.1-2SYNTHESISMETHOD#1.Loopthrougheach

390'frequencygeneratingtheentirelengthofthesineandcosine400'waves,andaddthemtotheaccumulatorsignal,XX[]

410'

420FORK%=0TO256'K%loopsthrougheachsampleinREX[]and

IMX[]

430FORI%=0TO511'I%loopsthrougheachsampleinXX[]440'

450XX[I%]=XX[I%]+REX[K%]*COS（2*PI*K%*I%/N%）

460XX[I%]=XX[I%]+IMX[K%]*SIN（2*PI*K%*I%/N%）

470'

480NEXTI%

490NEXTK%

500'

510END

图1-4IDCT示意图

图1-4解释了IDCT的过程以及频率域与反变换时振幅的不同。

图1-4a中是我们需要进行转换的时间域曲线，在0点坐标处振幅为32的一条曲线；图1-4b是进行DFT变换后的曲线，实数部分（ReX）的值为32，虚数部分的值全部为0，因此这里没有画虚数部分的曲线；公式1-3将频率域信号（图1-4b所示）转换为余弦函数的振幅（图1-4c所示）。

虚数部分（用正弦函数表示）的系数全部为0，因此这里没有显示。

频率域与三角函数振幅之所以不同，是因为频率域被定义为谱密度（spectraldensity）。

图1-4显示的是一个由32个点组成的信号在频率域中的实数部分，由编号从0到16的17个采样点组成。

谱密度是指单位带宽所能表达的信号量（振幅），其计算方法是使用三角函数的振幅除以相应的带宽（bandwidth）。

图1-4中的虚线解释了带宽的计算，即在采样点之间进行平均分割。

采样点0和16的带宽为1/N，其他采样点（1-15）的带宽为2/N。

这就是公式1-3中ReX[0]和ReX[N/2]与其他ReX不同的原因。

图1-5频率域的带宽（bandwidth）

DFT的分析与计算

DFT的计算有三种方法：

第一种是解线性方程祖，这种方法简单但计算量很大，实际应用中很少使用；第二种是关联法（correlation），基于已知的另一条的曲线；第三中方法是快速傅立叶变换（FFT），FFT算法将对一条含N个点曲线的计算转为对N条含1个点的曲线的计算，从而大大降低了计算量。

线性方程组求解DFT

使用这种方法来计算DFT是很自然的，从N个方程求解N个未知数。

但这种方法计算量很大，实际应用中很少使用。

关联法（correlation）求解DFT

通过correlation求解DFT是求解DFT的标准方法，下面使用一个例子来说明这种方法。

求解一个包含64个点的信号的DFT，意味着我们要计算频率域中实数部分的33个系数和虚数部分的33个系数。

在这个例子中，我们只解一个系数，ImX[3]。

ImX[3]是一条包含三个完整周期的正弦函数的振幅，这个正弦函数曲线分布在点0到点63之间，如图1-6a所示。

在图1-6中，a和b是两个时间域的示例信号，在这里分别称之为x1[]和x2[]。

曲线x1[]是一个包含3个完整周期、分布在0到63之间的正弦函数曲线；x2[]由多条正弦函数曲线和余弦函数曲线混合而成，在组成x2[]的三角函数曲线中，没有任何一条在0到63之间有完整的三个周期。

通过这两条曲线可以解释算法要实现的功能：

当输入函数为x1[]时，算法的计算结果应该是32，也就是信号中正弦曲线的振幅；而当输入函数为x2[]时，算法的计算结果应该为0，因为x2[]所表示的曲线并不在这个信号中。

之所以非x1[]的曲线与x1[]相乘结果为0，是因为除x1[]外的任意一个函数与正弦

函数相乘时，在0到63（3个完整周期）上的积分都为0。

在图1-6中，图e是图a和图c相乘的结果，将各个点的值相加即可得到32；图f是图b和图d相乘的结果，将各个点的值相加得到的结果为0。

上面的计算过程可以用公式1-4来表示。

公式1-4

图1-6关联法（correlation）求DFT

下面是关联法计算DFT的算法伪代码：

100'THEDISCRETEFOURIERTRANSFORM

110'Thefrequencydomainsignals,heldinREX[]andIMX[],arecalculatedfrom

120'thetimedomainsignal,heldinXX[].130'

140DIMXX[511]'XX[]holdsthetimedomainsignal

150DIMREX[256]'REX[]holdstherealpartofthefrequencydomain160DIMIMX[256]'IMX[]holdstheimaginarypartofthefrequency

domain

170'

180PI=3.14159265'Settheconstant,PI

190N%=512'N%isthenumberofpointsinXX[]200'

210GOSUBXXXX'MythicalsubroutinetoloaddataintoXX[]220'

230'

240FORK%=0TO256'ZeroREX[]&IMX[]sotheycanbeusedas

accumulators

250REX[K%]=0

260IMX[K%]=0

270NEXTK%

280'

290''CorrelateXX[]withthecosineandsinewaves,Eq.8-4300'

310FORK%=0TO256'K%loopsthrougheachsampleinREX[]and

IMX[]

320FORI%=0TO511'I%loopsthrougheachsampleinXX[]330'

340REX[K%]=REX[K%]+XX[I%]*COS（2*PI*K%*I%/N%）

350IMX[K%]=IMX[K%]-XX[I%]*SIN（2*PI*K%*I%/N%）

360'

370NEXTI%

380NEXTK%

390'

400END

二元性（Duality）

DFT和IDFT变换公式很类似。

从一个域到另一个域，都是用已有的值乘以基函数，然后将相应的值相加。

实际上，DFT和IDFT的区别仅仅是时间域中包含N个点，而频率域中包含N/2+1个点。

在复数傅里叶变换中，时间域和频率域中的信号都包含N个点，这使得两个域具有一种对称的性质，而在两个域之间的转换公式也就几乎一样了。

时间域和频率域的这种对称被称之为对称性（Duality），二元性可以产生很多有趣的性质。

例如：

在频率域中的一个单点对应于时间域中的一条三角函数曲线，由于Duality，这种性质反过来也成立，在时间域中的一个点对应于频率域中的一条三角函数曲线。

快速傅立叶变换（FastFourierTransform）

FFT算法是由J.W.Cooley和J.W.Tukey在论文”AnalgorithmforthemachinecalculationofcomplexFourierSeries”中提出的。

FFT是基于ComplexDFT来实现的。

通过ComplexDFT来计算RealDFT

尽管FFT算法是基于ComplexDFT实现的，但我们仍可以用其来计算RealDFT，因为RealDFT可以方便地转换为ComplexDFT。

从图2-1中可以看出RealDFT和ComplexDFT的区别。

在RealDFT中，时间域是一个包含N个点的信号，频率域则包括实数部分和虚数部分两个长度为N/2+1的信号；在ComplexDFT中，时间域也有两个部分，分别是实数部分和虚数部分，长度为N。

频率域的实数部分和虚数部分则长度增至N。

如图2-1所示，RealDFT和ComplexDFT的区别仅在于后者在时间域增加了一

个虚数部分，频率域长度的变化正是由这个虚数部分引起的。

图2-1RealDFT和ComplexDFT的区别

产生这个区别的原因是实数的虚数部分为0，因此将实数表达为虚数很简单，加上一个系数为0的虚数部分即可。

例如在图2-1中的ComplexDFT，若将时间域的虚数部分设为0，频率域中多出的部分也置为0，那么图2-1中的RealDFT和ComplexDFT就相等了。

当包含负频率时，DFT的频率域会具有周期性。

在ComplexDFT中，

频率域中0到N/2为正频率，N/2+1到N-1为负频率。

与使用ComplexDFT计算RealDFT相比，使用ComplexInverseDFT计算RealInverseDFT更为困难。

这是因为频率域中N/2+1到N-1部分的系数需要计算。

其计算过程也不复杂，系数N/2+1对应系数N/2-1的相反数，N/2+2对应N/2-2的相反数，即：

系数（N/2+1）=—系数（N/2-1）系数（N/2+2）=—系数（N/2-2）

注意，0与N/2没有相应的点与之对应。

进行RealInverseDFT计算时，首先将0到N/2复制到complexDFT的系数0到N/2，然后使用一个子过程来计算系数N/2+1到N-1。

这个子过程的伪代码实现如下：

6000'NEGATIVEFREQUENCYGENERATION

6010'Thissubroutinecreatesthecomplexfrequencydomainfromtherealfrequencydomain.

6020'Uponentrytothissubroutine,N%containsthenumberofpointsinthesignals,and

6030'REX[]andIMX[]containtherealfrequencydomaininsamples0toN/2.

6040'Onreturn,REX[]andIMX[]containthecomplexfrequencydomaininsamples0toN-1.

6050'

6060FORK%=（N%/2+1）TO（N%-1）

6070REX[K%]=REX[N%-K%]

6080IMX[K%]=-IMX[N%-K%]

6090NEXTK%

6100'

6110RETURN

FFT的实现原理

FFT算法很复杂，本文不讨论细节，只描述其实现原理。

在虚数域中，时间域和频率域表达的都是由N个虚数点组成的信号，每个虚数点都由实数部分和虚数部分的两个数字来表达。

例如虚数点X[6]，就是由实数部分ReX[6]和虚数部分ImX[6]组成。

FFT算法的核心思想是将时间域中一个包含N个点的信号分解为N个包含一个点的信号。

然后分别计算这N个信号的频率域对应值，最后将这N个频率域的信号综合为频率域中的一个信号。

图2-2描述了一个包含12个点的示例信号在FFT中的分解过程。

图2-2FFT中的分解（decompose）过程

图2-2中的过程看似复杂，实际上可以通过如图2-3所示的位反转算法（bitreversalsorting）来实现。

算法将各点的二进制位反转为对称的形式，即可完成N个点的信号到N个单点信号的分解过程。

图2-3位反转排序

FFT算法的下一步是分别求出这N个单点信号在频率域的振幅。

这是算法中最容易

的一步，单点的振幅等于它自己本身的值，这意味着在这一步什么也不必做。

算法的最后一步是将这N个频率域的点按在时间域分解时的反序结合（combine）起

来，这里不能使用位反转算法，这一步是算法中最复杂的部分。

图2-4展现了两个长度为4的频率域信号组合为一个长度为8的频率域信号的过

程。

组合（synthesis）的顺序必须与在时间域中分解（decompose）的过程完全相逆。

以时间域的信号abcd和信号efgh为例，要将其整合为一个包含8个点的信号需要经过这两步：

首先将这两个信号进行稀释（dilute），即用0填充为长度为8的信号，然后两者相加即可得到新的信号。

如abcd稀释后得到a0b0c0d0，efgh稀释后得到0e0f0g0h，两者相加可得abcdefgh。

图2-4FFT组合（synthesis）

当时间域用0稀释时，对应的频率域会复制自己。

当时间域先移位再用0填充时，对应的频率域会乘以一个三角函数，然后再复制自己。

abcd与efgh的稀释方法并不相同，abcd稀释为a0b0c0d0，其偶数位为0；efgh稀释为0e0f0g0h，其奇数位为0。

也就是说efgh向右移动了一位，这个在时间域的移位对应于频率域乘以一个三角函数。

图2-5展示了在两个频率域中长度为4的信号组合的过程。

左侧的Odd-FourPointFrequencySpectrum指的是对应奇数位为0的时间域信号的频率域信号，如EFGH；右侧的Even-FourPointFrequencySpectrum指的是对应偶数位为0的时间域信号的频率域信号，如ABCD。

为了更清楚地表达这个过程，图2-6将其中的两个点拿出来，因为这个图形很想一只张开翅膀的蝴蝶，因此人们也将这个图所代表的过程称之为butterfly。

图2-5FFT组合过程

图2-6Butterfly

图2-7显示了FFT变换的流程图，包含了FFT变换的三个部分。

1.时间域的分解过程可以通过位变换算法来实现。

2.将时间域分解后得到的N个单点转换为频率域并不需要任何计算，因为对于单点而言，在频率域的振幅等于时间域的振幅。

3.第三部分是整个算法的核心，是图中重点要表达的部分。

图2-7FFT流程图

在图2-7中，最外面的循环表示要在lgN个层次上进行组合（synthesis），中间那层循环指在每一层上的组合过程，最内部的循环表示butterfly过程。

下面是FFT算法的一段Basic代码：

1000'THEFASTFOURIERTRANSFORM

1010'Uponentry,N%containsthenumberofpointsintheDFT,REX[]and1020'IMX[]containtherealandimaginarypartsoftheinput.Uponreturn,1030'REX[]andIMX[]containtheDFToutput.Allsignalsrunfrom0toN%-1.1040'

1050PI=3.14159265'Setconstants1060NM1%=N%-1

1070ND2%=N%/2

1080M%=CINT（LOG（N%）/LOG

（2））

1090J%=ND2%

1100'

1110FORI%=1TON%-2'Bitreversalsorting1120IFI%>=J%THENGOTO1190

1130TR=REX[J%]

1140TI=IMX[J%]

1150REX[J%]=REX[I%]

1160IMX[J%]=IMX[I%]

1170REX[I%]=TR

1180IMX[I%]=TI

1190K%=ND2%

1200IFK%>J%THENGOTO1240

1210J%=J%-K%

1220K%=K%/2

1230GOTO1200

1240J%=J%+K%

1250NEXTI%

1260'

1270FORL%=1TOM%'Loopforeachstage1280LE%=CINT（2^L%）

1290LE2%=LE%/2

1300UR=1

1310UI=0

1320SR=COS（PI/LE2%）'Calculate