2层梁上顺下横顶托承重.docx

2层梁上顺下横顶托承重.docx

《2层梁上顺下横顶托承重.docx》由会员分享，可在线阅读，更多相关《2层梁上顺下横顶托承重.docx（16页珍藏版）》请在冰豆网上搜索。

2层梁上顺下横顶托承重

恒智天成安全计算软件梁模板（扣件钢管架支撑）计算书

恒智天成安全计算软件梁模板（扣件钢管架支撑）计算书依据《建筑施工模板安全技术规范》（JGJ162-2008）、《建筑施工计算手册》江正荣著、《建筑结构荷载规范》（GB50009-2001）、《混凝土结构设计规范》（GB50010-2002）、《钢结构设计规范》（GB50017-2003）等规范编制。

梁段：

L1。

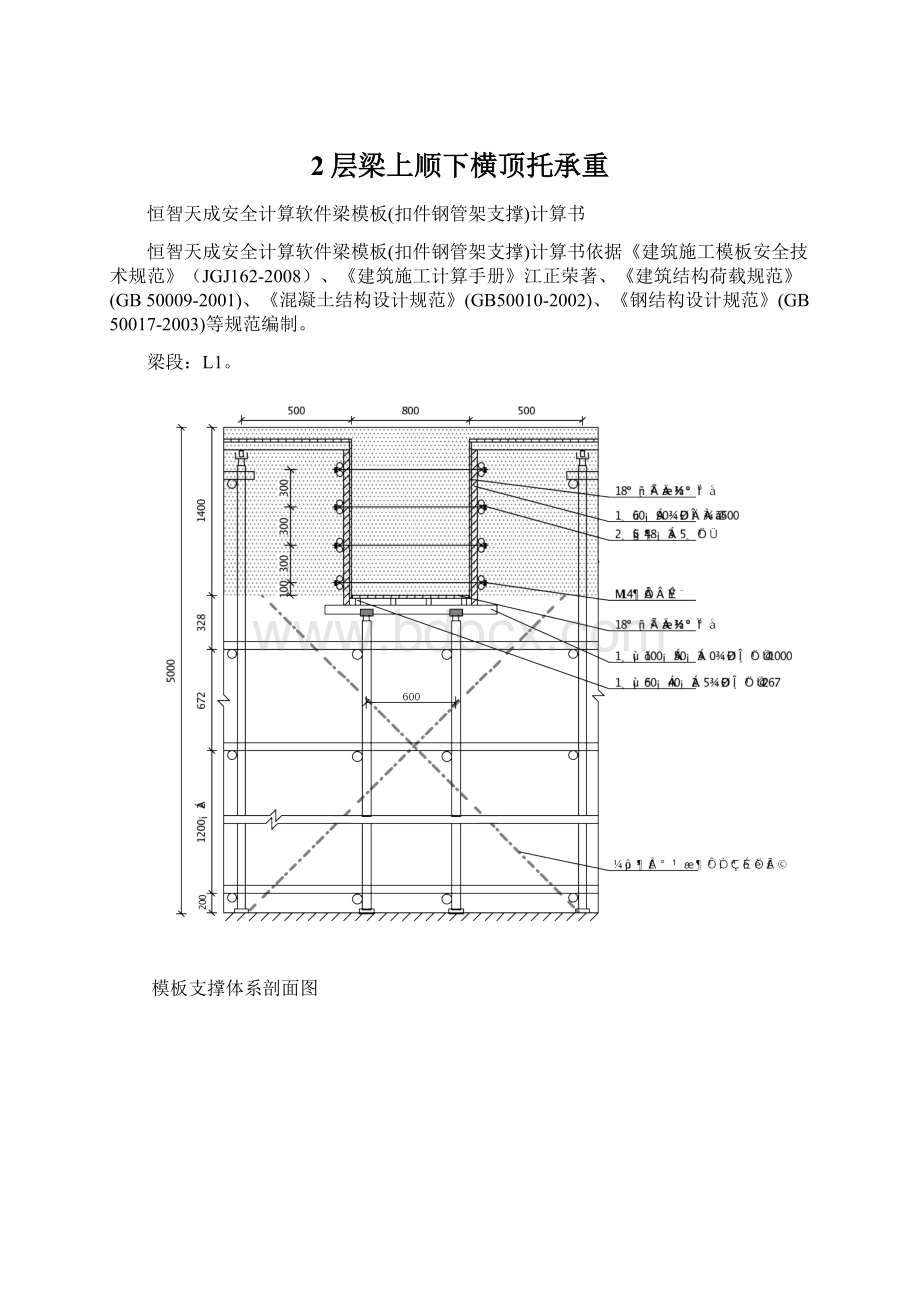
模板支撑体系剖面图

钢管排列平面示意图

一、参数信息

1.模板构造及支撑参数

（一）构造参数

梁截面宽度B：

0.8m；梁截面高度D：

1.4m；

楼层高度H：

5m；结构表面要求：

隐藏；

混凝土楼板厚度：

220mm；梁边至板支撑距离：

0.5m；

立杆沿梁跨度方向间距la：

1m；立杆步距h：

1.2m；

梁底承重立杆根数：

2；梁底两侧立杆间距lc：

0.6m；

梁底承重立杆间距（mm）依次是：

600；

（二）支撑参数

梁底采用的支撑钢管类型为：

Ф48×3.5mm；

钢管钢材品种：

钢材Q235钢（＞16-40）；钢管弹性模量E：

206000N/mm2；

钢管屈服强度fy：

235N/mm2；钢管抗拉/抗压/抗弯强度设计值f：

205N/mm2；

钢管抗剪强度设计值fv：

120N/mm2；钢管端面承压强度设计值fce：

325N/mm2；

2.荷载参数

新浇筑砼自重标准值G2k：

24kN/m3；钢筋自重标准值G3k：

1.5kN/m3；

梁侧模板自重标准值G1k：

0.5kN/m2；砼对模板侧压力标准值G4k：

12.933kN/m2；

倾倒砼对梁侧产生的荷载标准值Q3k：

2kN/m2；

梁底模板自重标准值G1k：

0.5kN/m2；振捣砼对梁底模板荷载Q2k：

2kN/m2；

3.梁侧模板参数

加固楞搭设形式：

主楞横向次楞竖向设置；

（一）面板参数

面板采用克隆（平行方向）18mm厚覆面木胶合板；厚度：

18mm；

抗弯设计值fm：

29N/mm2；弹性模量E：

11500N/mm2；

（二）主楞参数

材料：

2根Ф48×3.5钢管；

间距（mm）：

100,300*3；

钢材品种：

钢材Q235钢（＞16-40）；弹性模量E：

206000N/mm2；

屈服强度fy：

235N/mm2；抗拉/抗压/抗弯强度设计值f：

205N/mm2；

抗剪强度设计值fv：

120N/mm2；端面承压强度设计值fce：

325N/mm2；

（三）次楞参数

材料：

1根60×90矩形木楞；

间距（mm）：

500；

木材品种：

太平洋海岸黄柏；弹性模量E：

10000N/mm2；

抗压强度设计值fc：

13N/mm2；抗弯强度设计值fm：

15N/mm2；

抗剪强度设计值fv：

1.6N/mm2；

（四）加固楞支拉参数

加固楞采用穿梁螺栓支拉；

螺栓直径：

M14；螺栓水平间距：

800mm；

螺栓竖向间距（mm）依次是：

100,300*3；

4.梁底模板参数

搭设形式为：

2层梁上顺下横顶托承重；

（一）面板参数

面板采用克隆（平行方向）18mm厚覆面木胶合板；厚度：

18mm；

抗弯设计值fm：

29N/mm2；弹性模量E：

11500N/mm2；

（二）第一层支撑梁参数

材料：

1根□60×40×2.5矩形钢管；

根数：

4；

钢材品种：

钢材Q235钢（＞16-40）；弹性模量E：

206000N/mm2；

屈服强度fy：

235N/mm2；抗拉/抗压/抗弯强度设计值f：

205N/mm2；

抗剪强度设计值fv：

120N/mm2；端面承压强度设计值fce：

325N/mm2；

（三）第二层支撑梁参数

材料：

1根□100×50×3.0矩形钢管；

钢材品种：

钢材Q235钢（＞16-40）；弹性模量E：

206000N/mm2；

屈服强度fy：

235N/mm2；抗拉/抗压/抗弯强度设计值f：

205N/mm2；

抗剪强度设计值fv：

120N/mm2；端面承压强度设计值fce：

325N/mm2；

二、梁侧模板面板的计算

面板为受弯结构，需要验算其抗弯强度和刚度。

根据《模板规范（JGJ162-2008）》第5.2.1条规定，面板按照简支跨计算。

这里取面板的计算宽度为1.180m。

面板的截面惯性矩I和截面抵抗矩W分别为:

I=1180×183/12=5.735×105mm4；

W=1180×182/6=6.372×104mm3；

1.荷载计算及组合

（一）新浇砼作用于模板的最大侧压力G4k

按下列公式计算，并取其中的较小值:

F1=0.22γtβ1β2V1/2

F2=γH

其中γ--砼的重力密度，取24.000kN/m3；

t--新浇混凝土的初凝时间，取2.000h；

T--砼的入模温度，取20.000℃；

V--砼的浇筑速度，取1.500m/h；

H--砼侧压力计算位置处至新浇砼顶面总高度，取1.400m；

β1--外加剂影响修正系数，取1.000；

β2--砼坍落度影响修正系数，取1.000。

根据以上两个公式计算得到：

F1=12.933kN/m2

F2=33.600kN/m2

新浇砼作用于模板的最大侧压力G4k=min（F1，F2）=12.933kN/m2；

砼侧压力的有效压头高度：

h=F/γ=12.933/24.000=0.539m；

（二）倾倒砼时产生的荷载标准值Q3k

Q3k=2kN/m2；

（三）确定采用的荷载组合

计算挠度采用标准组合：

q=12.933×1.18=15.261kN/m；

计算弯矩采用基本组合：

q=max（q1，q2）=20.624kN/m；

由可变荷载效应控制的组合：

q1=0.9×（1.2×12.933+1.4×2）×1.18=19.455kN/m；

由永久荷载效应控制的组合：

q2=0.9×（1.35×12.933+1.4×0.7×2）×1.18=20.624kN/m；

2.面板抗弯强度计算

σ＝M/W<[f]

其中：

W--面板的截面抵抗矩，W=6.372×104mm3；

M--面板的最大弯矩（N·mm）M=0.125ql2=6.445×105N·mm；

计算弯矩采用基本组合:

q=20.624kN/m；

面板计算跨度:

l=500.000mm；

经计算得到，面板的受弯应力计算值:

σ=6.445×105/6.372×104=10.114N/mm2；

实际弯曲应力计算值σ=10.114N/mm2小于抗弯强度设计值[f]=29N/mm2，满足要求！

3.面板挠度计算

ν=5ql4/（384EI）≤[ν]

其中：

q--作用在模板上的压力线荷载:

q=15.261kN/m；

l-面板计算跨度:

l=500.000mm；

E--面板材质的弹性模量:

E=11500N/mm2；

I--面板的截面惯性矩:

I=5.735×105mm4；

容许挠度:

结构表面隐藏[ν]=l/250=2.000mm；

面板的最大挠度计算值:

ν=5×15.261×500.0004/（384×11500×5.735×105）=1.883mm；

实际最大挠度计算值:

ν=1.883mm小于最大允许挠度值:

[ν]=2.000mm，满足要求！

三、梁侧模板支撑的计算

1.次楞计算

次楞采用1根60×90矩形木楞为一组，间距500mm。

次楞的截面惯性矩I，截面抵抗矩W和弹性模量E分别为：

I=1×364.5×104=3.645×106mm4；

W=1×81×103=8.100×104mm3；

E=10000N/mm2；

（一）荷载计算及组合

计算挠度采用标准组合：

q=12.933×0.500=6.467kN/m；

计算弯矩和剪力采用基本组合：

有效压头高度位置荷载：

q=max（q1，q2）=8.739kN/m；

由可变荷载效应控制的组合：

q1=0.9×（1.2×12.933+1.4×2）×0.500=8.244kN/m；

由永久荷载效应控制的组合：

q2=0.9×（1.35×12.933+1.4×0.7×2）×0.500=8.739kN/m；

有效压头高度位置以下荷载：

q=0.9×1.35×12.933×0.500=7.857kN/m；

顶部荷载：

q=0.9×1.4×0.7×2×0.500=0.882kN/m；

（二）内力计算

次楞直接承受模板传递的荷载，根据实际受力情况进行电算，得到计算简图及内力、变形图如下：

弯矩和剪力计算简图

弯矩图（kN·m）

剪力图（kN）

变形计算简图

变形图（mm）

经过计算得到:

最大弯矩M=0.065kN·m

最大剪力：

V=1.265kN

最大变形：

ν=0.005mm

最大支座反力：

F=2.485kN

（三）次楞计算

（1）次楞抗弯强度计算

σ=M/W=0.065×106/8.100×104=0.806N/mm2

实际弯曲应力计算值σ=0.806N/mm2小于抗弯强度设计值[f]=15N/mm2，满足要求！

（2）次楞抗剪强度计算

τ=VS0/Ib=1.265×1000×60750/（3.645×106×60）=0.351N/mm2；

实际剪应力计算值0.351N/mm2小于抗剪强度设计值[fv]=1.600N/mm2，满足要求！

（3）次楞挠度计算

容许挠度:

结构表面隐藏[ν]=l/250；

第1跨最大挠度为0.001mm，容许挠度为0.400mm，满足要求！

第2跨最大挠度为0.005mm，容许挠度为1.200mm，满足要求！

第3跨最大挠度为0.004mm，容许挠度为1.200mm，满足要求！

第4跨最大挠度为0.003mm，容许挠度为1.200mm，满足要求！

第5跨最大挠度为0.003mm，容许挠度为0.720mm，满足要求！

各跨实际最大挠度计算值小于最大允许挠度值，满足要求！

2.主楞计算

主楞采用2根Ф48×3.5钢管为一组，共4组。

主楞的截面惯性矩I，截面抵抗矩W和弹性模量E分别为：

I=2×12.19×104=2.438×105mm4；

W=2×5.08×103=1.016×104mm3；

E=206000N/mm2；

主楞承受次楞传递的集中力，计算弯矩和剪力时取次楞的最大支座力2.485kN，计算挠度时取次楞的最大支座力2.047kN。

根据实际受力情况进行电算，得到计算简图及内力、变形图如下：

弯矩和剪力计算简图

弯矩图（kN·m）

剪力图（kN）

变形计算简图

变形图（mm）

经过计算得到:

最大弯矩M=0.354kN·m

最大剪力：

V=3.200kN

最大变形：

ν=0.255mm

最大支座反力：

F=4.443kN

（1）主楞抗弯强度计算

σ=M/W=0.354×106/1.016×104=34.834N/mm2

实际弯曲应力计算值σ=34.834N/mm2小于抗弯强度设计值[f]=205N/mm2，满足要求！

（2）主楞抗剪强度计算

τ=VS0/Itw=1.600×1000×6946/（2.438×105×3.5）=13.026N/mm2；

实际剪应力计算值13.026N/mm2小于抗剪强度设计值[fv]=120.000N/mm2，满足要求！

（3）主楞挠度计算

容许挠度:

结构表面隐藏[ν]=l/250；

第1跨最大挠度为0.255mm，容许挠度为3.200mm，满足要求！

第2跨最大挠度为0.027mm，容许挠度为3.200mm，满足要求！

第3跨最大挠度为0.254mm，容许挠度为3.200mm，满足要求！

各跨实际最大挠度计算值小于最大允许挠度值，满足要求！

3.穿梁螺栓计算

验算公式如下:

N<[N]=f×A

其中N--穿梁螺栓所受的拉力；

A--穿梁螺栓有效面积（mm2）；

f--穿梁螺栓的抗拉强度设计值，取170N/mm2；

穿梁螺栓型号:

M14；查表得：

穿梁螺栓有效直径:

11.55mm；

穿梁螺栓有效面积:

A=105mm2；

穿梁螺栓最大容许拉力值:

[N]=170×105/1000=17.850kN；

穿梁螺栓所受的最大拉力:

N=4.443kN。

穿梁螺栓所受的最大拉力N=4.443kN小于穿梁螺栓最大容许拉力值[N]=17.850kN，满足要求！

四、梁底模板面板计算

面板为受弯结构，需要验算其抗弯强度和刚度。

根据《模板规范（JGJ162-2008）》第5.2.1条规定，面板按照简支跨计算。

这里取面板的计算宽度为1.000m。

面板的截面惯性矩I和截面抵抗矩W分别为:

I=1000×183/12=4.860×105mm4；

W=1000×182/6=5.400×104mm3；

1.荷载计算及组合

模板自重标准值G1k=0.5×1.000=0.500kN/m；

新浇筑砼自重标准值G2k=24×1.000×1.4=33.600kN/m；

钢筋自重标准值G3k=1.5×1.000×1.4=2.100kN/m；

永久荷载标准值Gk=G1k+G2k+G3k=36.200kN/m；

振捣砼时产生的荷载标准值Q2k=2×1.000=2.000kN/m；

（1）计算挠度采用标准组合：

q=36.200kN/m；

（2）计算弯矩采用基本组合：

q=max（q1，q2）=45.747kN/m；

由可变荷载效应控制的组合：

q1=0.9×（1.2×36.200+1.4×2.000）=41.616kN/m；

由永久荷载效应控制的组合：

q2=0.9×（1.35×36.200+1.4×0.7×2.000）=45.747kN/m；

2.面板抗弯强度验算

σ＝M/W<[f]

其中：

W--面板的截面抵抗矩，W=5.400×104mm3；

M--面板的最大弯矩（N·mm）M=0.125ql2=4.066×105N·mm；

计算弯矩采用基本组合:

q=45.747kN/m；

面板计算跨度:

l=800/（4-1）=266.667mm；

经计算得到，面板的受弯应力计算值:

σ=4.066×105/5.400×104=7.530N/mm2；

实际弯曲应力计算值σ=7.530N/mm2小于抗弯强度设计值[f]=29N/mm2，满足要求！

3.面板挠度验算

ν=5ql4/（384EI）≤[ν]

其中：

q--作用在模板上的压力线荷载:

q=36.200kN/m；

l-面板计算跨度:

l=266.667mm；

E--面板材质的弹性模量:

E=11500N/mm2；

I--截面惯性矩:

I=4.860×105mm4；

[ν]-容许挠度:

结构表面隐藏[ν]=l/250=1.067mm；

面板的最大挠度计算值:

ν=5×36.200×266.6674/（384×11500×4.860×105）=0.426mm；

实际最大挠度计算值:

ν=0.426mm小于最大允许挠度值:

[ν]=1.067mm，满足要求！

五、梁底支撑梁的计算

1.第一层支撑梁的计算

支撑梁采用1根□60×40×2.5矩形钢管，共4组，均匀布置在梁底。

支撑梁的截面惯性矩I，截面抵抗矩W和弹性模量E分别为：

I=1×21.88×104=2.188×105mm4；

W=1×7.29×103=7.290×103mm3；

E=206000N/mm2；

支撑梁直接承受模板传递的荷载，按照均布荷载作用下的三跨连续梁计算。

支撑梁均布荷载计算：

（1）计算弯矩和剪力采用（考虑支撑梁自重）：

q=45.747×266.667/1000.000+0.048=12.248kN/m；

（2）计算挠度采用（考虑支撑梁自重）：

q=36.200×266.667/1000.000+0.036=9.689kN/m；

最大弯矩M=0.1ql2=0.1×12.248×12=1.225kN.m

最大剪力V=0.6ql=0.6×12.248×1=7.349kN

最大支座力N=1.1ql=1.1×12.248×1=13.472kN

最大变形ν=0.677ql4/100EI=0.677×9.689×10004/（100×206000.000×2.188×105）=1.455mm

（一）支撑梁抗弯强度计算

σ=M/W=1.225×106/7.290×103=168.006N/mm2

实际弯曲应力计算值σ=168.006N/mm2小于抗弯强度设计值[f]=205N/mm2，满足要求！

（二）支撑梁抗剪计算

τ=VS0/Itw=7.349×1000×3578/（2.188×105×2.5）=48.068N/mm2；

实际剪应力计算值48.068N/mm2小于抗剪强度设计值[fv]=120.000N/mm2，满足要求！

（三）支撑梁挠度计算

最大挠度：

ν=1.455mm；

[ν]-容许挠度:

结构表面隐藏[ν]=l/250=4.000mm；

实际最大挠度计算值:

ν=1.455mm小于最大允许挠度值:

[ν]=4.000mm，满足要求！

2.第二层支撑梁的计算

支撑梁采用1根□100×50×3.0矩形钢管，间距1000mm。

支撑梁的截面惯性矩I，截面抵抗矩W和弹性模量E分别为：

I=1×112.12×104=1.121×106mm4；

W=1×22.42×103=2.242×104mm3；

E=206000N/mm2；

（一）荷载计算及组合：

（1）第二层支撑梁承受第一层支撑梁传递的集中力

计算弯矩和剪力时取第一层中部支撑梁传递的最大支座力13.472kN；

计算弯矩和剪力时取第一层端部支撑梁传递的最大支座力7.612kN；（包含梁侧模板传递的自重荷载）

计算挠度时取第一层中部支撑梁传递的最大支座力10.658kN；

计算挠度时取第一层端部支撑梁传递的最大支座力5.978kN；（包含梁侧模板传递的自重荷载）

（2）第二层支撑梁自重均布荷载：

计算弯矩和剪力时取0.092kN/m；

计算挠度时取0.068kN/m。

（二）支撑梁验算

根据前面计算的荷载组合，取结构最不利状态进行电算，得到计算简图及内力、变形图如下：

弯矩和剪力计算简图

弯矩图（kN·m）

剪力图（kN）

变形计算简图

变形图（mm）

经过计算得到从左到右各支座力分别为：

N1=21.131kN

N2=21.131kN

计算得到：

最大弯矩：

M=1.487kN.m

最大剪力：

V=13.500kN

最大变形：

ν=0.194mm

最大支座反力：

F=21.131kN

（1）支撑梁抗弯强度计算

σ=M/W=1.487×106/2.242×104=66.320N/mm2

实际弯曲应力计算值σ=66.320N/mm2小于抗弯强度设计值[f]=205N/mm2，满足要求！

（2）支撑梁抗剪计算

τ=VS0/Itw=13.500×1000×8502/（1.121×106×3）=34.123N/mm2；

实际剪应力计算值34.123N/mm2小于抗剪强度设计值[fv]=120.000N/mm2，满足要求！

（3）支撑梁挠度计算

[ν]-容许挠度:

结构表面隐藏[ν]=l/250；

第1跨最大挠度为0.157mm，容许挠度为0.800mm，满足要求！

第2跨最大挠度为0.194mm，容许挠度为2.400mm，满足要求！

第3跨最大挠度为0.157mm，容许挠度为0.800mm，满足要求！

各跨实际最大挠度计算值小于最大允许挠度值，满足要求！

六、立杆的稳定性计算

立杆的稳定性计算公式

σ=N/（φA）≤[f]

其中σ--钢管立杆轴心受压应力计算值（N/mm2）；

N--立杆的轴心压力设计值，它包括：

纵向钢管的最大支座反力：

N1=21.131kN；

脚手架钢管的自重：

N2=0.9×1.2×0.149×（5-1.4）=0.579kN；

N=N1+N2=21.131+0.579=21.709kN；

φ--轴心受压立杆的稳定系数，由长细比lo/i查《模板规范JGJ162-2008》附录D得到φ=0.714；

立杆计算长度lo=1.2m；

计算立杆的截面回转半径i=1.580cm；

A--立杆净截面面积：

A=4.890cm2；

[f]--钢管立杆抗压强度设计值：

[f]=205N/mm2；

钢管立杆长细比λ计算值：

λ=lo/i=1.2×100/1.580=75.949

钢管立杆长细比λ=75.949小于钢管立杆允许长细比[λ]=150，满足要求！

钢管立杆受压应力计算值：

σ=21.709×103/（0.714×4.890×102）=62.152N/mm2；

钢管立杆稳定性计算σ=62.152N/mm2小于钢管立杆抗压强度的设计值[f]=205N/mm2，满足要求！