高一数学两平面的平行判定和性质检测试题.docx
《高一数学两平面的平行判定和性质检测试题.docx》由会员分享,可在线阅读,更多相关《高一数学两平面的平行判定和性质检测试题.docx(21页珍藏版)》请在冰豆网上搜索。
高一数学两平面的平行判定和性质检测试题
典型例题一
例1:
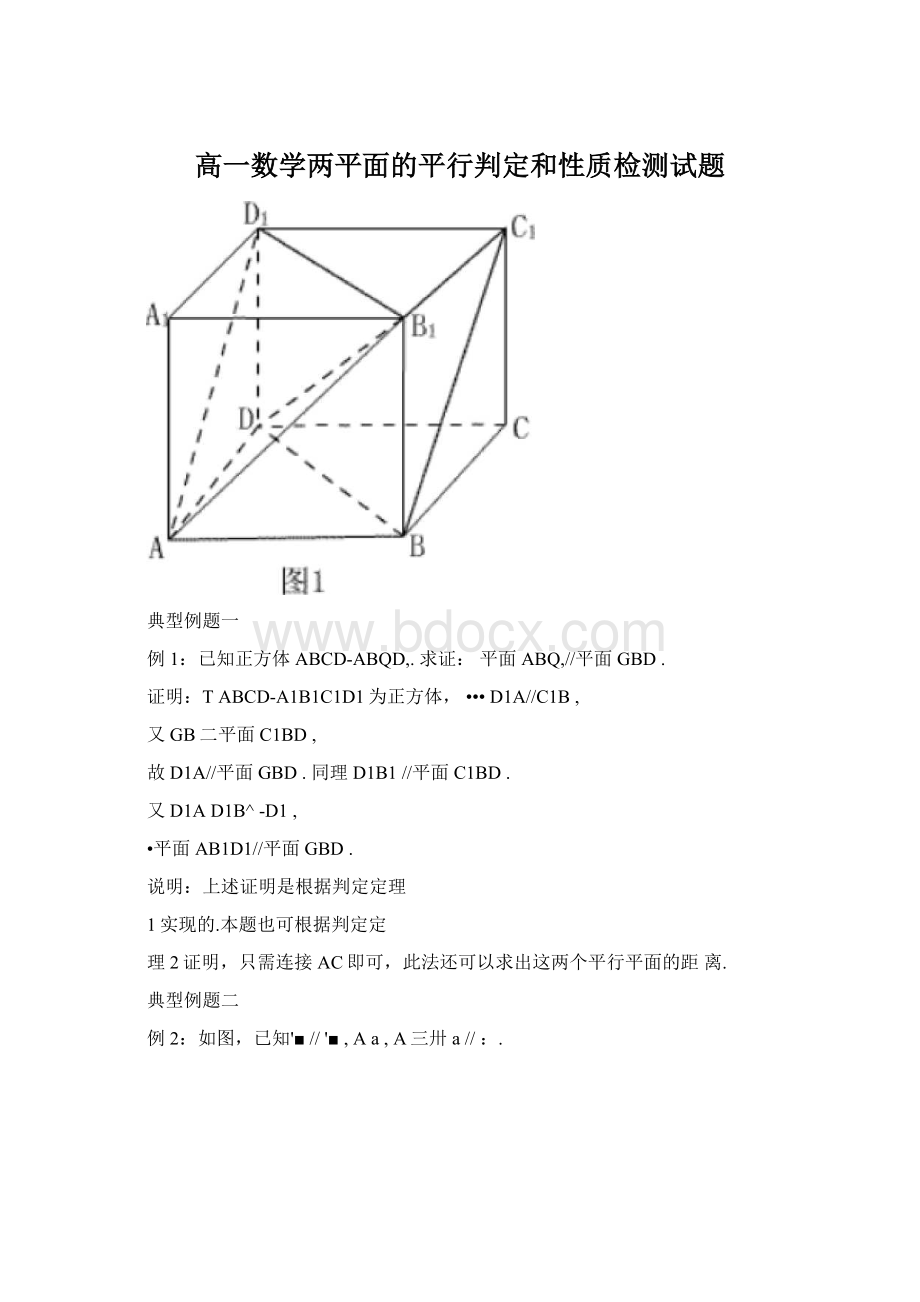
已知正方体ABCD-ABQD,.求证:
平面ABQ,//平面GBD.
证明:
TABCD-A1B1C1D1为正方体,•••D1A//C1B,
又GB二平面C1BD,
故D1A//平面GBD.同理D1B1//平面C1BD.
又D1AD1B^-D1,
•平面AB1D1//平面GBD.
说明:
上述证明是根据判定定理
1实现的.本题也可根据判定定
理2证明,只需连接AC即可,此法还可以求出这两个平行平面的距离.
典型例题二
例2:
如图,已知'■//'■,Aa,A三卅a//:
.
证明:
过直线a作一平面,
:
=耳,-=b.
TI
•a^/b
又a/L
在同一个平面内过同一点A有两条直线a,ai与直线b平行
二a与ai重合,即a二:
-.
说明:
本题也可以用反证法进行证明.
典型例题三
例3:
如果一条直线与两个平行平面中的一个相交,那么它和另一个也相交.
已知:
如图,〉//I“A.
求证:
丨与]相交.
证明:
在[上取一点B,过I和B作平面,由于与a有公共点A,
与1有公共点B.
二与〉、[都相交.
设=a,:
=b.
T:
//'■
/.a//b
又I、a、b都在平面内,且I和a交于A.
TI与b相交.
所以I与1相交.
典型例题四
例4:
已知平面:
//-,AB,CD为夹在a,
CD的中点.
求证:
EF//■,EF//-.
证明:
连接AF并延长交[于G.
•/AGCD=F
•••AG,CD确定平面,且:
=AC,
'■=DG.
,所以AC//DG,
.ACF=/GDF,
又.AFC"DFG,CF=DF,
△ACF也厶DFG.
•AF=FG.
又AE=BE,
•••EF//BG,BG
故EF//.
同理EF//:
说明:
本题还有其它证法,要点是对异面直线的处理.
典型例题六
例6如图,已知矩形ABCD的四个顶点在平面上的射影分别为
A、Bi、Ci、Di,且A、Bi、Ci、Di互不重合,也无三点共线.
形.
证明:
TAA_〉,DDi_:
■
二AA//DDi
不妨设AA和DDi确定平面1.同理BBi和CG确定平面.
又AA〃BB,且BBi
二AA〃
同理AD//
又AAAD=A
'-//
又口仃0=ADi,□仃Y=BiCi
…AiDi//BiCi.
同理AiBi//CiDi.
.四边形AiBiCiDi是平行四边形.
典型例题七
例7设直线l、m,平面:
、,下列条件能得出:
「的是().
A.I二汽,m二汽,且l//'-,m/「B.I二:
z,m二,,且l//m
C.l_:
•,m.I匸,且l//mD.\II工,m//-,且l〃m
分析:
选项A是错误的,因为当l//m时,:
•与[可能相交.选项
B是错误的,理由同A.选项C是正确的,因为l_〉,m〃l,所以m_:
・,又//■.选项D也是错误的,满足条件的:
可能与1相交.
答案:
C
说明:
此题极易选A,原因是对平面平行的判定定理掌握不准确所致.
本例这样的选择题是常见题目,要正确得出选择,需要有较好的作图能力和对定理、公理的准确掌握、深刻理解,同时要考虑到各种情况.
典型例题八
例8设平面:
•一平面,平面1一平面,且:
1分别与相交于a、b,a//b.求证:
平面:
//平面一:
.
分析:
要证明两平面平行,只要设法在平面:
上找到两条相交直线,或作出相交直线,它们分别与-平行(如图).
证明:
在平面〉内作直线PQ_直线a,在平面一:
内作直线MN_直
•••平面〉—平面,
/.PQ_平面,MN—平面,
/.PQ//MN.
又;a〃p,PQa二Q,MNb二N,
「•平面〉〃平面一:
.
说明:
如果在〉、1内分别作PQ_,MN_,这样就走了弯路,还需证明PQ、MN在:
•、[内,如果直接在:
•、1内作a、b的垂线,就可推出PQ//MN.
由面面垂直的性质推出“线面垂直”,进而推出“线线平行”、“线面平行”,最后得到“面面平行”,最后得到“面面平行”.其核心是要形成应用性质定理的意识,在立体几何证明中非常重要.
典型例题九
例9如图所示,平面:
//平面[,点A>C:
点B、D「,AB二a是〉、[的公垂线,CD是斜线.若AC二BD二b,CD二c,M、N分别是AB和CD的中点,
(1)求证:
MN//一:
;
(2)求MN的长.
分析:
(1)要证MN//1,取AD的中点P,只要证明MN所在的平面PMN11■:
.为此证明PM111,PNI/'■-即可.⑵要求MN之长,在:
CMA中,CM、CN的长度易知,关键在于证明MN_CD,从而由勾股定理可以求解.
证明:
(1)连结AD,设P是AD的中点,分别连结PM、PN.
•/M是AB的中点,•••PMIIBD.
又BD一:
,二PMII-.
同理TN是CD的中点,二PNIIAC.
•/AC二:
;,二PNIT..
T:
II■-,PNPM=P,二平面PMNII■-.
•/MN平面PMN,二MNII'-.
(2)分别连结MC、MD.
1
・AC二BD二b,AM二BMa
2'
又TAB是:
、]的公垂线,二■CAM=/DBM=90,
/.RtACM坐RtBDM,二CM=DM,
•••BMC是等腰三角形.
又N是CD的中点,•MN_CD.
在RtCMN中,MN*CM2-CN2J•4b2a2-c2.
2
说明:
(1)证“线面平行”也可以先证“面面平行”,然后利用面面平行的性质,推证“线面平行”,这是一种以退为进的解题策略.
(2)空间线段的长度,一般通过构造三角形、然后利用余弦定理或勾股定理来求解.
(3)面面平行的性质:
①面面平行,则线面平行;②面面平行,则
被第三个平面所截得的交线平行.
线线平行线面平行毘二面面平行
典型例题十
例10如果平面〉内的两条相交直线与平面1所成的角相等,那么这两个平面的位置关系是:
分析:
按直线和平面的三种位置关系分类予以研究.解:
设a、b是平面〉内两条相交直线.
(1)若a、b都在平面1内,a、b与平面1所成的角都为0,这时〉与[重合,根据教材中规定,此种情况不予考虑.
(2)若a、b都与平面[相交成等角,且所成角在(0,90)内;
Ta、b与:
有公共点,这时:
-与:
相交.
若a、b都与平面[成90角,则a//b,与已知矛盾.此种情况不可能.
(3)若a、b都与平面1平行,则a、b与平面一:
所成的角都为0,〉内有两条直线与平面1平行,这时〉//'■.
综上,平面〉>-的位置关系是相交或平行.
典型例题十一
例11试证经过平面外一点有且只有一个平面和已知平面平行.
已知:
A'平面〉,
求证:
过A有且只有一个平面
分析:
“有且只有”要准确理解,要先证这样的平面是存在的,再证它是惟一的,缺一不可.
证明:
在平面内任作两条相交直线a和b,则由A-一知,A「a,A-b.
点A和直线a可确定一个平面M,点A和直线b可确定一个平面
N.
在平面M、N内过A分别作直线a//a、b'//b,
故a、b是两条相交直线,可确定一个平面:
.
Ta二:
,a二:
二,a//a,二a〃:
.
同理b//-.
又a'1,b',a'b'二A,A■-//-..
所以过点A有一个平面1/八.
假设过A点还有一个平面//--,
则在平面:
内取一直线c,A-c,点A、直线c确定一个平面1由公理2知:
:
「二m,『=n,
Am//c,n//c,
又Am,An,
这与过一点有且只有一条直线与已知直线平行相矛盾,因此假设不成立,
所以平面1只有一个.
所以过平面外一点有且只有一个平面与已知平面平行.
典型例题十二
例12已知点S是正三角形ABC所在平面外的一点,且
SA=SB=SC,SG为ASAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF内的位置关系,并给予证明
分析1:
如图,观察图形,即可判定SG//平面DEF,要证明结论成立,只需证明SG与平面DEF内的一条直线平行.
观察图形可以看出:
连结CG与DE相交于H,连结FH,FH就是适合题意的直线.
怎样证明SG//FH?
只需证明H是CG的中点.
B
证法1:
连结CG交DE于点H,
TDE是-ABC的中位线,
/.DE//AB
在ACG中,D是AC的中点,且DH//AG,
二H为CG的中点.
•/FH是SCG的中位线,二FH//SG.
又SG二平面DEF,FH平面DEF,
/.SG〃平面DEF.
分析2:
要证明SG//平面DEF,只需证明平面SAB//平面DEF,要证明平面DEF//平面SAB,只需证明SA//DF,SB//EF而SA//DF,SB//EF可由题设直接推出.
证法2:
VEF为:
SBC的中位线,
/.EF//SB.
VEF二平面SAB,SB平面SAB,
/.EF//平面SAB.
同理:
DF//平面SAB,EFDF=F,
平面SAB//平面DEF,又VSG平面SAB,
二SG//平面DEF.
典型例题十三
例13如图,线段PQ分别交两个平行平面〉、1于A、B两点,线段PD分别交于C、D两点,线段QF分别交〉、[于F、E两点,若PA=9,AB=12,BQ=12,■ACF的面积为72,求^BDE的面积.
分析:
求-BDE的面积,看起来似乎与本节内容无关,事实上,已
知ACF的面积,若BDE与ACF的对应边有联系的话,可以利用
ACF的面积求出BDE的面积.
解:
T平面QAF「;;,=AF,平面QAF卄:
BE,
又T:
/「J.AF//BE.
同理可证:
AC//BD,/.FAC与.EBD相等或互补,即sin.FAC=sin.EBD.
由FA//BE,得BE:
AF二QB:
QA=12:
24=1:
2,
.BE=1AF
2
由BD//AC,得:
AC:
BD=PA:
PB=9:
21=3:
7,二BD=7AC
3
1
又•/ACF的面积为72,即-AFACsin.FAC=72.
2
.1
--SDBEBEBDsin_EBD
117
AF—ACsin.FAC
223
71AFACsin•FAC
62=772=84.
6
.ABDE的面积为84平方单位.
说明:
应用两个平行的性质一是可以证明直线与直线的平行,二是可以解决线面平行的问题.注意使用性质定理证明线线平行时,定第三个平面与两个平行平面相交,其交线互相平行.
典型例题十四
例14在棱长为a的正方体中,求异面直线BD和B,C之间的距离.
分析:
通过前面的学习,我们解决了如下的问题:
若a和b是两条
异面直线,则过a且平行于b的平面必平行于过b且平行于a的平
面.我们知道,空间两条异面直线,总分别存在于两个平行平面内.因
此,求两条异面直线的距离,有时可以通过求这两个平行平面之间的距离来解决.
具体解法可按如下几步来求:
①分别经过BD和BiC找到两个互相平等的平面;②作出两个平行平面的公垂线;③计算公垂线夹在两个平等平面间的长度.
解:
如图,
BD//BP
=平面ABD//平面CB1D1
根据正方体的性质,易证:
AB//DQ
连结ACi,分别交平面ABD和平面CBiDi于M和N
因为CG和AG分别是平面ABCD的垂线和斜线,AC在平面ABCD内,AC_BD
由三垂线定理:
AG—BD,同理:
AG_AD
AG—平面ABD,同理可证:
AG—平面CB1D1
二平面ABD和平面CBiDi间的距离为线段MN长度.
如图所示:
在对角面AG中,Oi为AG的中点,O为AC的中点
/.AM=MN二NC=1A°=3a
3
3°
说明:
关于异面直线之间的距离的计算,有两种基本的转移方法:
①转化为线面距.设a、b是两条异面直线,作出经过b而和a平行的平面〉,通过计算a和〉的距离,得出a和b距离,这样又回到点面距离的计算;②转化为面面距,设a、b是两条异面直线,作出经过b而和a平行的平面:
•,再作出经过a和b平行的平面「通过计算〉、1之间的距离得出a和b之间的距离.
典型例题十五
例15正方体ABCD-ABQDi棱长为a,求异面直线AC与BG的距
离.
解法1:
(直接法)如图:
取BC的中点P,连结PD、PBi分别交AC、BCi于M、N两点,
易证:
DB1//MN,DB1—AC,DB1_BG.
二MN为异面直线AC与BC1的公垂线段,易证:
MN-a.
33
小结:
此法也称定义法,这种解法是作出异面直线的公垂线段来解.但通常寻找公垂线段时,难度较大.
解法2:
(转化法)如图:
•/AC//平面A1C1B,
二AC与BCi的距离等于AC与平面ACiB的距离,
在RtOBOi中,作斜边上的高OE,则OE长为所求距离,
VOB2a,00i二a,
2
二O1B=
OiB
faOE-00^-三a.
■2OiB3
小结:
这种解法是将线线距离转化为线面距离.
解法3:
(转化法)如图:
T平面ACD1//平面A,GB,
二AC与BCi的距离等于平面ACDi与平面ACiB的距离.
TDBi—平面ACDi,且被平面ACDi和平面AGB三等分;
二所求距离为1B1D3a.
33
小结:
这种解法是线线距离转化为面面距离.
解法4:
(构造函数法)如图:
任取点QBCi,作QR_BC于R点,作PK_AC于K点,设RC二x,贝卩BR二QR二a—x,CK=KR,且KR2CK^CR2
二KR2JcR2Jx2.
22
则QK2=1x2(a-x)2
2
3(2、21212
(xa)aa,
2333
[3
故QK的最小值,即AC与BCi的距离等于山a.
3
小结:
这种解法是恰当的选择未知量,构造一个目标函数,通过求这个函数的最小值来得到二异面直线之间的距离.
解法5:
(体积桥法)如图:
当求AC与BCi的距离转化为求AC与平面AGB的距离后,设C点到平面A,GB的距离为h,
则Vc.A1C1B=VA_BCS•
「h「3C、2a)2Ja1a2,
3432
h—a.即AC与BC1的距离等于一3a•
33
小结:
本解法是将线线距离转化为线面距离,再将线面距离转化为锥体化为锥体的高,然后用体积公式求之.这种方法在后面将要学到.
说明:
求异面直线距离的方法有:
(1)(直接法)当公垂线段能直接作出时,直接求.此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.
(2)(转化法)把线线距离转化为线面距离,如求异面直线a、b距离,先作出过a且平行于b的平面—则b与〉距离就是a、b距离.(线面转化法).
也可以转化为过a平行b的平面和过b平行于a的平面,两平行平面的距离就是两条异面直线距离.(面面转化法).
(3)(体积桥法)利用线面距再转化为锥体的高用何种公式来求.
(4)(构造函数法)常常利用距离最短原理构造二次函数,利用求二次函数最值来解.
两条异面直线间距离问题,教科书要求不高(要求会计算已给出公垂线时的距离),这方面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.
典型例题十六
例16如果〉/】,AB和AC是夹在平面〉与]之间的两条线段,
AB_AC,且AB=2,直线AB与平面:
.所成的角为30,求线段AC长
的取值范围.
解法1:
如图所示:
作AD_一:
于D,连结BD、CD、BC
TABBD,AC■DC,AB2AC^BC2,
.•.在BDC中,由余弦定理,得:
•/AD_:
.ABD是AB与]所在的角.
TAB=2,
.AD=1,BD=.3,DC—.AC2-1,
.—3+AC2_1_4_AC2门日仃c••一1・2:
:
0,即:
0
23.AC2-1
•AV,即AC长的取值范围为竽
解法2:
如图:
•/AB_AC
二AC必在过点A且与直线AB垂直的平面内
设丁盲:
丨,则在内,当AC_丨时,AC的长最短,且此时
AC=ABtanZABC
23
ABtan30=
3
而在内,C点在l上移动,远离垂足时,AC的长将变大,
从而AC_2卫,
3
即AC长的取值范围是0^,+^.
.3丿
说明:
(1)本题考查直线和直线、直线和平面、平面和平面的位置关系,对于运算能力和空间想象能力有较高的要求,供学有余力的同
学学习.
(2)解法1利用余弦定理,采用放缩的方法构造出关于AC长的不等式,再通过解不等式得到AC长的范围,此方法以运算为主.
(3)解法2从几何性质角度加以解释说明,避免了繁杂的运算推导,但对空间想象能力要求很高,根据此解法可知线段AC是连结异面直线AB和丨上两点间的线段,所以AC是AB与丨的公垂线段时,其长最短.
典型例题十七
例17如果两个平面分别平行于第三个平面,那么这两个平面互
相平行.
已知:
〉//,■-//,求证:
〉/厂:
.
分析:
本题考查面面平行的判定和性质定理以及逻辑推理能力.由
于两个平面没有公共点称两平面平行,带有否定性结论的命题常用反证法来证明,因此本题可用反证法证明.另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线,利用线线平行来推理证明面面平行,或者也可以证明这两个平面同时垂直于某一直线.
证明一:
如图,
假设〉、1不平行,则〉和]相交.
和:
至少有一个公共点A,即Ahf,A:
T:
//,'■//,
•••A:
.
于是,过平面外一点A有两个平面〉、1都和平面平行,这和“经过平面外一点有且只有一个平面与已知平面平行”相矛盾,假设不成立。
•:
//1.
证明二:
如图,在平面:
内任取一点A,过A点作直线I与〉相交.
V:
//,二丨与也相交.
V'■!
/,二丨与1也相交.
过丨作两相交平面分别与:
•交于直线mi、m,且与m2、门2,交于
直线m3、.
v:
//,二m//m3.
V:
//,二m2//m3.
m//m2.
V叶二:
m2:
,
二m//:
同理n//'.
又vm口=a,m、m二:
;
:
//:
.
T:
//,二丨_.
•/■-//,二丨_一:
.
二:
•//-.
说明:
证明两个平面平行,可根据定义、应用判定定理来证明.
典型例题十八
例18如图,已知a、b是异面直线,求证:
过a和b分别存在平面〉和:
,使〉//-.
分析:
本题考查面面平行及线面垂直的判定和综合推理能力.根
据前面学过的知识,过异面直线中的一条有且仅有一个平面与另一条
平行.这样过a和b分别有平面与另一条线平行.那么这两个平面是不是互相平行呢?
这两个平面是不是就是我们所要找的:
和]?
证明:
在直线a上任取一点P,过P点作直线b'〃b.
故过a和b'可确定一平面记为:
在直线b上任取一点Q.
过Q点作直线a'//a.
同理过b和a'可确定一平面,记为二
I
Ta//a,aua,
a1/二.同理b/r.
Ta,:
,b:
,a'b=Q.
•「//I.
说明:
由此题结论可知,两异面直线必定存在于两个互相平行的
平面中.所以两异面直线间的距离就可转化为两平行平面间的距离
(本题易证a和b的公垂线段垂直于两平行平面).