第四章线性系统参数估计的最小二乘法.pdf

第四章线性系统参数估计的最小二乘法.pdf

《第四章线性系统参数估计的最小二乘法.pdf》由会员分享，可在线阅读，更多相关《第四章线性系统参数估计的最小二乘法.pdf（16页珍藏版）》请在冰豆网上搜索。

第四章第四章线性系统参数估计的最小二乘法线性系统参数估计的最小二乘法4.1引言引言最小二乘（LeastSquares）法是用于参数估计的数学方法，它使数学模型在误差平方和最小的意义上拟合实验数据。

1801年，意大利天文学家朱赛普皮亚齐发现了第一颗小行星谷神星。

经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。

随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。

时年24岁的高斯也计算了谷神星的轨道。

奥地利天文学家海因里希奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。

高斯使用的最小二乘法的方法发表于1809年他的著作天体运动论中，而法国科学家勒让德于1806年独立发现“最小二乘法”，但因不为时人所知而默默无闻。

勒让德曾与高斯为谁最早创立最小二乘法原理发生争执。

1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明，因此被称为高斯-马尔可夫定理。

此后LS法成了处理观测所得实验数据的有力工具。

现在成为辨识的主要算法。

最小二乘辨识是一种一致的、无偏的、有效的方法4.2基本最小二乘方法基本最小二乘方法4.2.1最小二乘曲线拟合4.2.1最小二乘曲线拟合最小二乘技术提供给我们一个数学程序，通过它能获得一个在最小方差意义上与实验数据拟合最好的模型。

假定有一个变量Y，它与一个n维变量X=（x1,x2,xn）是线性关系，即Y=1x1+2x2+nxn（4.1）其中，=（1,2,n）是一个参数集。

在系统辨识中它们是未知的。

我们希望通过不同时刻对Y及X的观测值来估计出它们的数值。

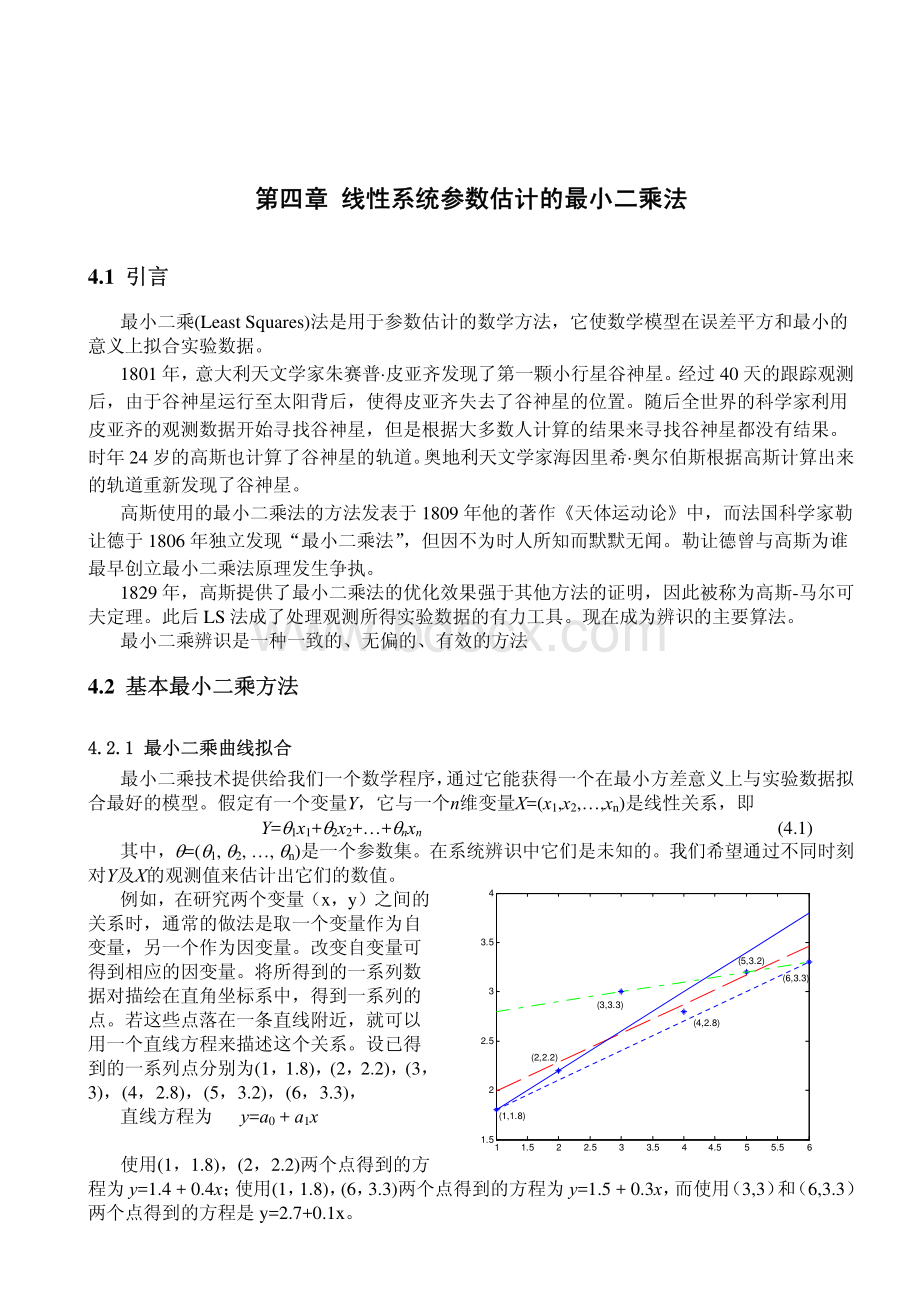
例如，在研究两个变量（x，y）之间的关系时，通常的做法是取一个变量作为自变量，另一个作为因变量。

改变自变量可得到相应的因变量。

将所得到的一系列数据对描绘在直角坐标系中，得到一系列的点。

若这些点落在一条直线附近，就可以用一个直线方程来描述这个关系。

设已得到的一系列点分别为（1，1.8），（2，2.2），（3，3），（4，2.8），（5，3.211.522.533.544.555.561.522.533.54（1,1.8）（2,2.2）（3,3.3）（4,2.8）（5,3.2）（6,3.3），（6，3.3），直线方程为y=a0+a1x使用（1，1.8），（2，2.2）两个点得到的方程为y=1.4+0.4x；使用（1，1.8），（6，3.3）两个点得到的方程为y=1.5+0.3x，而使用（3,3）和（6,3.3）两个点得到的方程是y=2.7+0.1x。

从图中可看到，前两条线都仅能满足两个点的要求，而对其它点的误差都很大，其6个点的误差平方累计分别为0.49和0.42。

第三条线能满足三个点的要求，但误差平方累计更大，为1.58。

显然我们需要找到一条更为理想的直线来取得较小的误差。

例如图中的红色短划线，它的方程为y=1.697+0.294x，误差平方累计为0.25。

这条线是怎样得到的呢？

它是用最小二乘法得到的。

下面讨论更为一般的情况。

假设在t1,t2,tm时刻对Y及X的观测值序列已经被我们获得，并且用y（i）,x1（i）,x2（i）,x3（i）,i=1,2,m来表示这些观测数据。

显然，可以用m个方程组来表示量测数据与估计值之间的关系（4.2）+=+=+=）（）（）（）（）2（）2（）2（）2（）1（）1（）1（）1（221122112211mxmxmxmyxxxyxxxynnnnnnLMLL写成矩阵形式，为Y=X（4.3）其中1）（）1（=mmyyYMnmnnmxmxxxX=）（）（）1（）1（11LMML11=nnM根据m相对n的大小不同，可能有三种情况：

1）mn如果无任何测量误差和噪声，也应有唯一解。

但它们是不可避免的，这样就可能造成无解的情况。

例:

对于系统2211xxy+=，采样得任取其中2个方程都可解得212121373241221；若有测量噪声或误差，则无解。

212121301.7324995.0005.2；12；-2-因为此时实际方程变为+=XY，在这种情况下只能求近似解。

通常使用的方法为最小平方误差法4.2.2最小二乘估计准则和正则方程4.2.2最小二乘估计准则和正则方程已知+=XY（4.4）则误差应为XY（4.5）设目标函数或估计的判据为误差的平方=miiTJ12（4.6）取J最小为优化指标XXXYYXYYXYXYJTTTTTTT+=）（）（2121998.0004.221；将J对微分并令其为零（关于矩阵微分的方法见附录），有022=XXYXJTTYXXXTT=（4.7）得（4.8）YXXXTT1）（这样求得的就称为的最小二乘估计（LSE），在统计学上，方程（4.7）称为正则方程，称为残差。

在前面讨论的例子中，把6个数据对分别代入直线方程y=a0+a1x中可得到1个由6个直线方程构成的方程组XY=，其中各参数分别为；=10aaTY3.32.38.232.28.1=；。

将这些参数分别代入式（4.8）解出TX=654321111111294.0;687.110=aa，并可求出误差向量XY=。

误差的平方和为253.0*=例例4.1测得铜导线在温度时的电阻）（CTio）（iR如表6-1，求电阻R与温度T的近似函数关系。

i1234567）（CTio19.125.030.136.040.045.150.0）（iR76.3077.8079.2580.8082.3583.9085.10解:

解:

画出散点图，可见测得的数据接近一条直线，故取n=1，拟合函数为TaaR10+=于是可列出方程组-3-+=+=+=）7（）7（）2（）2（）1（）1（101010TaaRTaaRTaaRM写成最小二乘标准格式为+=XY，其中TRY10.8590.8335.8280.8025.7980.7730.76=TX=0.501.450.400.361.300.251.191111111=10aa解方程组得YXXXTT1）（=572.700=a292.01=a故得R与T的拟合直线为TR292.0572.70+=利用上述关系式，可以预测不同温度时铜导线的电阻值。

例如，由R=0得T=-242.5，即预测温度T=-242.5时，铜导线无电阻。

4.2.3最小二乘估计的几何解释4.2.3最小二乘估计的几何解释Yx1xmY已知最小二乘输出估计向量;输出估计误差向量如图（输出残差向量）XY=YY=；输入测量矩阵=TmTTxxxXM21输出估计向量Y是输出测量Y在由x1,x2,xm所张成的空间上的正交投影，或者说，输出残差向量垂直于由x1,x2,xm所张成的空间。

这个几何解释说明，输出向量Y可以分解成属于估计空间的估计向量Y和垂直于估计空间的输出残差向量。

最小二乘估计的解的形式为最小二乘估计的解的形式为（4.9）YXXXTT1）（=很显然，只有正则方程的逆存在才能有解。

而正则方程的逆存在（或者说最小二乘估计的解存在）的充分必要条件为：

过程的输入信号必须是2n阶持续激励信号。

这个条件又被称为开环可辩识条件。

它意味着辩识所用的输入信号不能任意选择，否则就可能造成系统不可辩识。

通常所用的信号有

（1）随机序列（如白噪声）；

（2）伪随机序列（如M序列）；（3）离散序列（对含有n种其频率不是倍频关系的正弦信号的组合信号进行采样所得到的离散序列）；4.3最小二乘在线性系统参数估计中的应用最小二乘在线性系统参数估计中的应用（差分方程辩识）（差分方程辩识）4.3.1线性系统模型的参数估计4.3.1线性系统模型的参数估计在连续系统中，系统的动态特性可用微分方程来描述，在离散系统中，系统的动态特性则用差分方程来描述。

对于n阶系统，它的差分方程可写为（4.10）（）（）（）（11kuqBkyqA=传递函数可表示为）（）（）（）（）（111=qAqBkukyqH（4.11）其中A,B分别是引入向后移位算子q-1的多项式（4.12）nnqaqaqA+=L1111）（nnqbqbbqB+=L1101）（式（4.10）可写为）（）1（）（）（）1（）（101nkubkubkubnkyakyakynn+=+LL-4-对有测量误差的系统，则有（4.13）（）（）（）（）（11kkuqBkyqA+=通过移项，还可写为）（）（）（）（01kikubikyakyniinii+=）（）（kkXT+=（4.14）当观测得到的输出输入数据为2n+1个时（也就是n+1次观测后），可写出）（,）,（）,（,）,1（nkukunkykyXT=LL（4.15）这时被辩识参数。

当对输入输出观测了N+n次后，就可建立起有N个方程的方程组（N2n），即,101nnTbbbaaLL=+=XY（4.16）；+=）（）2（）1（NnynynyYM+=）（）2（）1（NnnnM；+=）（）2（）1（NnXnXnXXTTTM+=）（）（）（）1（）2（）2（）2（）1（）1（）1（）1（）（NuNnuNyNnyunuynyunuynyLLMMMMLLLL（4.17）这样我们就可以用前面介绍的最小二乘法求得估计量YXXXTT1）（=例例4.2已知一个二阶系统的传递函数为22111101）（+=zazazbbzH，在其输入端加入M序列输入后所得到的输出输入数据见下表，请利用这些数据辨识出系统的传递函数的系数。

k12345678910输入u1011001110输出y-0.45-0.011.152.561.92-0.30-0.800.912.922.40解：

解：

已知系统阶数n=2，有4个未知数。

将式（4.4）展开）1（）（）2（）1（）（1021+=kubkubkyakyaky根据要求，观测次数N2n+1，取N为6，k=3-5-=91.08.03.092.156.215.1）8（）7（）6（）5（）4（）3（yyyyyyY=113.08.00192.13.00056.292.11015.156.21101.015.10145.001.0）7（）8（）6（）7（）6（）7（）5（）6（）5（）6（）4（）5（）4（）5（）3（）4（）3（）4（）2（）3（）2（）3（）1（）2（uuyyuuyyuuyyuuyyuuyyuuyyX=57.089.076.088.0）（11021YXXXbbaaTT21176.088.0157.089.0）（+=zzzzH当N取8时有21177.088.0156.090.0）（+=zzzzH；当N取80时有21178.088.0157.094.0）（+=zzzzH而其真值为2118.09.015.01）（+=zzzzH例例4.3如图所示的一个差分方程系统，已知A为二阶,B为零阶，结构如下：

B（z-1）u（t）y（t）w（t）v（t）+A（z-1）=+=1）

（1）（122111zBzazazA其200次测量的最后10次观测数据为观测次数k191192193194195196197198199200观测输出Y0.580.530.550.610.550.530.550.550.590.54系统输入U0.790.770.760.840.780.760.760.780.810.77请用最小二乘辨识一次完成算法辨识多项式A的系数。

解：

解：

已知系统的传递函数为221111111）（）（）（）（）（+=zazazAzBkukyzH将其展开后为）（）2（）1（）（21kukyakyaky=+;写成标准最小二乘格式后成为）（）2（）1（）（21kukyakyaky+