10第3章单元和单元插值函数.pdf

10第3章单元和单元插值函数.pdf

《10第3章单元和单元插值函数.pdf》由会员分享，可在线阅读，更多相关《10第3章单元和单元插值函数.pdf（12页珍藏版）》请在冰豆网上搜索。

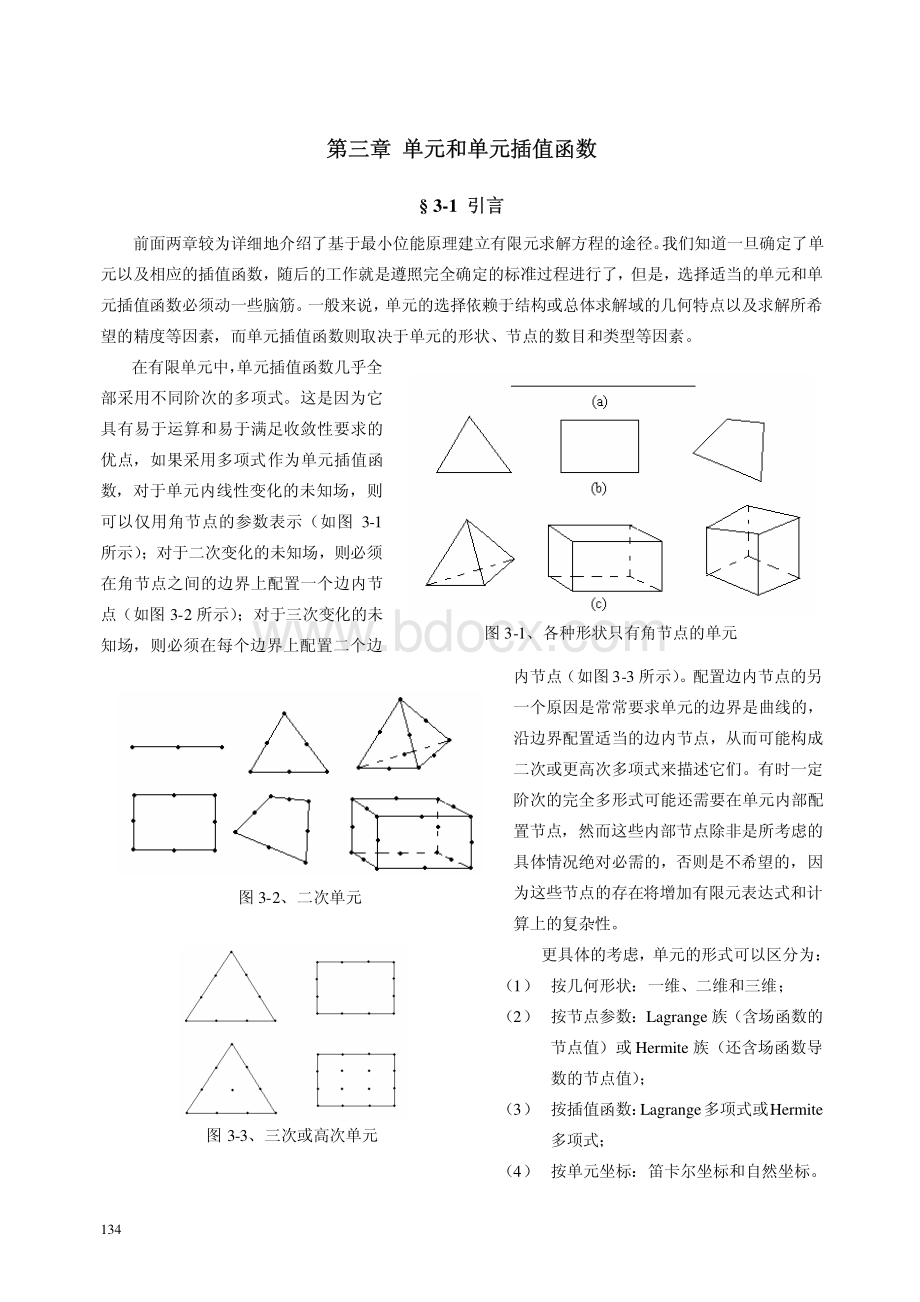
134第三章第三章单元和单元插值函数单元和单元插值函数3-1引言引言前面两章较为详细地介绍了基于最小位能原理建立有限元求解方程的途径。

我们知道一旦确定了单元以及相应的插值函数，随后的工作就是遵照完全确定的标准过程进行了，但是，选择适当的单元和单元插值函数必须动一些脑筋。

一般来说，单元的选择依赖于结构或总体求解域的几何特点以及求解所希望的精度等因素，而单元插值函数则取决于单元的形状、节点的数目和类型等因素。

在有限单元中，单元插值函数几乎全部采用不同阶次的多项式。

这是因为它具有易于运算和易于满足收敛性要求的优点，如果采用多项式作为单元插值函数，对于单元内线性变化的未知场，则可以仅用角节点的参数表示（如图3-1所示）；对于二次变化的未知场，则必须在角节点之间的边界上配置一个边内节点（如图3-2所示）；对于三次变化的未知场，则必须在每个边界上配置二个边内节点（如图3-3所示）。

配置边内节点的另一个原因是常常要求单元的边界是曲线的，沿边界配置适当的边内节点，从而可能构成二次或更高次多项式来描述它们。

有时一定阶次的完全多形式可能还需要在单元内部配置节点，然而这些内部节点除非是所考虑的具体情况绝对必需的，否则是不希望的，因为这些节点的存在将增加有限元表达式和计算上的复杂性。

更具体的考虑，单元的形式可以区分为：

（1）按几何形状：

一维、二维和三维；

（2）按节点参数：

Lagrange族（含场函数的节点值）或Hermite族（还含场函数导数的节点值）；（3）按插值函数：

Lagrange多项式或Hermite多项式；（4）按单元坐标：

笛卡尔坐标和自然坐标。

图3-1、各种形状只有角节点的单元图3-2、二次单元图3-3、三次或高次单元1353-2一维单元一维单元如大家熟知的杆单元或弯曲梁单元，实质上是两种形式的一维单元：

杆单元的节点参数中只包含场函数（表示杆单元的位移u）的节点值，单元内的场函数可以插值表示为2211NN（3-2-1）其中1N，2N是插值函数（或称形函数），lxN11，lxN2。

另一种弯曲梁单元的节点参数中，除包含场函数（表示弯曲梁单元的位移v）的节点值外，还包含场函数导数dxd的节点值。

单元内的场函数可以插值表示为24231211dxdNNdxdNN（3-2-2）其中插值函数为232433223232233221232231lxlxNlxlxNlxlxxNlxlxN实际上这两种单元就是以下将讨论的Lagrange单元和Hermite单元的最简单形式，现对它们的一般形式进行讨论。

一、Lagrange单元对于具有n个节点的一维单元，如果它的节点参数中只含有场函数的节点值，则单元内的场函数可插值表示为niiiN1（3-2-3）其中插值函数具有以下性质ijjixN，niixN11（3-2-3a）关于插值函数xNi的构造，为避免繁琐的推导，不必按前一章中所述的步骤进行，可以直接采用Lagrange插值多项式。

对于n个节点的一维单元，xNi可采用1N次Lagrange插值多项式，即niiiiiiiniijijnijjixxxxxxxxxxxxxxxxxxxxxxxxN11211121,1（3-2-4）表示二项式在j的范围内（niij,1,1,2,1）的乘积，n是单元的节点数，nxxx,21是n个节点的坐标。

如果2n，并且令01x，lx2，则插值函数xNi就可得到与式（3-2-1）完全一样的结果。

如果引入无量纲坐标lxxxxxxn111（3-2-5）136其中l表示单元的长度，则式（3-2-4）可表示为jijnijjiN,1（3-2-6）当2n时，且01，12，则有12121N，1212N（3-2-7）如果无量纲坐标采用另一种形式111022xxxxxxxxxnnn（3-2-8）其中210nxxx是单元中心坐标，则对于2n，有1211N，1212N（3-2-9）上述两种无量纲表示都是常用的形式。

为了今后方便地构造其他形式的Lagrange单元，在此可将式（3-2-6）改写成ijjnijjiffN,1（3-2-10）其中jjf表示任一点至点j的距离，也是j点坐标j表示成方程形式0jjf的左端项。

显然可见0jjf，从而保证了0jiN（ij）这一要求的满足。

jiijf是点i的坐标代入jf后得到的数值，这一因子引入的分母，是为了保证1iiN这一要求的满足。

理解jf和jijf的意义，对今后构造其他形式Lagrange单元的插值函数是有帮助的。

二、Hermite单元如果希望单元间的公共节点上还保持场函数导数的连续性，则节点参数还应包含场函数导数的节点值。

这时可采用Hermite多项式作为单元的插值函数。

对于只有两个端节点的一维单元（如弯曲梁单元），场函数采用Hermite多项式的插值函数可表示为21）1（21）0（iiiiiiddHH（3-2-11）其中Hermite多项式具有以下性质ijijiiijjijjddHHddHH）1（）1（）0（）0（00（3-2-11a）当01，12时）0（iH和）1（iH有以下形式的三次多项式13723）1（2432）0（2332）1（1232）0（11232231HNHNHNHN（3-2-12）以上在端部结点最高保持场函数的一阶导数连续的Hermite多项式称为一阶Hermite多项式。

零阶Hermite多项式即为Lagrange多项式，推而广之，在节点上保持至函数的n阶导数连续的Hermite多项式称为n阶Hermite多项式。

在两个节点的情况下，它是的12n次多项式。

函数的二阶Hermite多项式插值函数表示为2122）2（21）1（21）0（iiiiiiiiiddHddHH（3-2-13）3-3二维单元二维单元一、三角形单元在上一章中我们已讨论了三结点的三角形单元。

如同一维单元的情况，我们可以利用笛卡尔坐标，也可以利用无量纲的自然坐标来构造三角形单元的插值函数。

利用笛卡尔坐标构造三角形单元的插值函数在上一章中已讨论过，为确定插值函数中的各个系数涉及矩阵求逆运算。

对于高阶单元，此运算比较麻烦，因此普遍应用自然（面积）坐标来直接构造一般三角形单元的插值函数，这时运算比较简单。

从上一章的讨论中可知，对于三节点三角形单元，当引入面积坐标AALii（3,2,1i）（3-3-1）则单元插值函数可以表示为iiLN（3,2,1i）（3-3-2）如将由（3-2-10）式引入的对Lagrange插值函数各个因子的几何解释推广到现在的情况，则可以比较方便地利用面积坐标构造二次以及更高的三角形单元。

1、二次单元如图3-4所示，二次单元有六个节点，各节点的面积坐标分别住在括号内。

参照（3-2-10）式可将需要的插值函数表示成21321）（321）（,jiiiijijiLLLfLLLfN（3-3-3）其中321）（,LLLfij是通过除结点i以外所有节点的两根直线方程0,321）（LLLfij的左端项。

例如当1i时，）1（jf分别是通过节点4，6的直线方程021,1321）1（1LLLLf和通过节点3，5，2的直线方程0,1321）1（1LLLLf的左端项；iiiijLLLf321）（,中的iL1，iL2，iL3是节点i的面积坐标。

所以根据（3-3-3）可得111111212121LLLLN图3-4、自然坐标三角形单元（二次变化）138同理可得六节点三角形单元的其他插值函数如下。

333332222212121211212121LLLLNLLLLN131363232521214421214212142121LLLLNLLLLNLLLLN2、三次单元为了保证二维域三次多项式的完全性，三次单元应有10个节点，如图3-5所示，可根据二次单元相同的步骤，构造10节点三角形单元的插值函数。

对于角节点有iiiiiiiLLLLLLN231321132313132（3,2,1i）（3-3-4）对于边内节点1329132922151214LLLNLLLN1329132933272326LLLNLLLN1329132913193318LLLNLLLN对于中心节点3213211027313131LLLLLLN如有需要，可以构造更高次的三角形单元，其步骤是

（1）按二维域内各次完全多项式的要求确定节点的数目（n）和位置，此要求可表示如Pascal三角形如图3-6所示。

（2）按广义的Lagrange插值多项式构造插值函数，即pjiiiijijiLLLfLLLfN1321）（321）（,（3-3-5）其中p为插值次数。

显然，按上式构造的插值函数满足ijjjjiLLLN321,这一要求。

另外，由于iN的上述性质，以及节点数目和配置符合Pascal三角形的要求，可以证明这种单元场函数是满足收敛准则的。

图3-5、自然坐标三角形单元（三次变化）图3-6、Pascal三角形139二、Lagrange矩形单元和Hermite矩形单元如果所研究问题的总体域是矩形的，采用矩形单元比三角形单元更为有效。

为了构造矩形单元的插值函数，开始总可以利用笛卡尔坐标的多项式xyyx3210（3-3-6）式中所包含的项数应等于单元的节点数。

但为了进一步确定上式中的系数,2,1,0ii，将涉及矩阵求逆运算，而且在某些情况下逆矩阵并不存在，因此更经常用的是利用自然坐标直接建立插值函数。

方法是将一维的Lagrange单元和Hermite单元加以推广，用来构造二维的Lagrange矩形单元和Hermite矩形单元。

1、Lagrange矩形单元构造任意的Lagrange矩形单元插值函数的一个简单而系统的方法是利用二个坐标方向适当方次Lagrange多项式的乘积。

现考虑如图3-7所示单元，其中一系列节点布置在1r列、1p行的规则网格上。

现在需要构造和布置在I列J行节点i相应的插值函数iN，我们已知Lagrange多项式rIIIIIIIrIIrIl11101110）（在第I列节点上等于1，而在其它列节点上等于0。

同理pJJJJJJJpJJpJl11101110）（在第J行节点上等于1，而在其它行节点上等于0。

从以上分析可知，所需要构造的插值函数应是）（）（pJrIIJillNN（3-3-7）iN在节点i上等于1，而在其余所有结点上等于0。

这种单元每一边上的节点数和函数在边界上的变化是协调。

因而也保证了单元之间函数的连续性。

如图3-8所示是三种形式的Lagrange矩形单元。

虽然构造它们的插值函数是很容易的，但是这类单元存在一定的缺点，主要是出现了随插值方次而增加的内节点，从而增加了单元的自由度，而这些自由度的增加通常并不能提高单元的精度。

如果我们考察图3-7、Lagrange矩形单元的一个典型插值函数（5r，4p，1I，4J）图3-8、Lagrange矩形单元（a）线性（b）二次（c）三次140pr的情况，从基于Pascal三角形的图3-9可以看出增加了很多不必要的高阶项，因为单元的精度通常是由完全多项式的方次决定的，因此后面将要讨论的Serendipity单元在实际中得到了比Lagrange单元更多的应用。

2、Hermite矩形单元一维的Hermite多项式也可以用和构造Lagrange单元相类似的方法，用来构造Hermite矩形单元的插值函数。

对于双1阶（3次）Hermite多项式，参考图3-10所示，可得161iiiQN（3-3-8）其中）0

（1）1（12）0

（1）0（11HHNHHN）1

（1）1（14）1

（1）0（13HHNHHN）0

（1）1（26）0

（1）0（25HHNHHN）1

（1）1（28）1

（1）0（27HHNHHN）0

（2）1（110）0

（2）0（19HHNHHN）1

（2）1（112）1

（2）0（111HHNHHN）0

（2）1（214）0

（2）0（213HHNHHN）1

（2）1（216）1

（2）0（215HHN