明管结构计算书.doc
《明管结构计算书.doc》由会员分享,可在线阅读,更多相关《明管结构计算书.doc(11页珍藏版)》请在冰豆网上搜索。
明管结构计算书
项目名称_____________日期_____________
设计者_____________校对者_____________
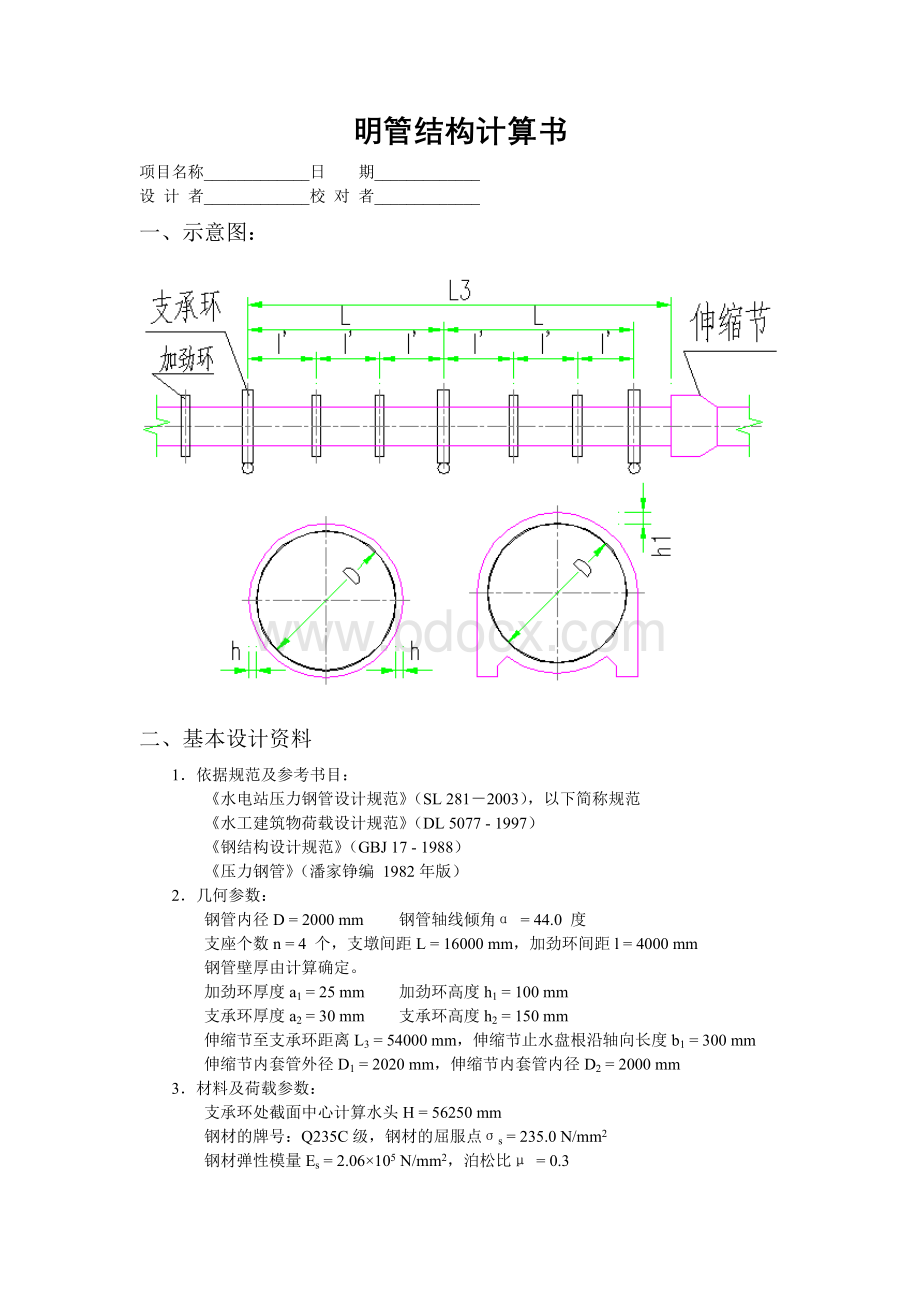
一、示意图:
二、基本设计资料
1.依据规范及参考书目:
《水电站压力钢管设计规范》(SL281-2003),以下简称规范
《水工建筑物荷载设计规范》(DL5077-1997)
《钢结构设计规范》(GBJ17-1988)
《压力钢管》(潘家铮编1982年版)
2.几何参数:
钢管内径D=2000mm 钢管轴线倾角α=44.0度
支座个数n=4个,支墩间距L=16000mm,加劲环间距l=4000mm
钢管壁厚由计算确定。
加劲环厚度a1=25mm 加劲环高度h1=100mm
支承环厚度a2=30mm 支承环高度h2=150mm
伸缩节至支承环距离L3=54000mm,伸缩节止水盘根沿轴向长度b1=300mm
伸缩节内套管外径D1=2020mm,伸缩节内套管内径D2=2000mm
3.材料及荷载参数:
支承环处截面中心计算水头H=56250mm
钢材的牌号:
Q235C级,钢材的屈服点σs=235.0N/mm2
钢材弹性模量Es=2.06×105N/mm2,泊松比μ=0.3
钢材线膨胀系数αs=1.20×10-5/℃,重度γs=7.85×10-5N/mm3
焊缝系数φ=0.95,支座对管壁摩擦系数f=0.10
伸缩节止水填料与管壁摩擦系数μ1=0.30
三、初估管壁厚度
1.按锅炉公式初估管壁厚度t:
根据末跨跨中计算水头并考虑将刚才允许应力降低15%,锅炉公式如下:
t=γwH1D/{2φ(1-0.15)[σ]}
末跨跨中管道中心计算水头H1=H-L/2×sinα
=56250-16000/2×sin44.0°=50693mm
[σ]=0.55σs=0.55×235.0=129.3N/mm2
t=9.80×10-6×50693×2000/[2×0.95(1-0.15)×129.25]=4.8mm
考虑2mm的锈蚀裕量后管壁厚度初定为t=7.0mm
2.复核管壁厚度是否满足制造工艺、安装、运输等要求所需刚度的最小厚度要求:
判断公式如下:
t≥D/800+4
则t应满足t≥2000/800+4=6.5mm
实际选用管壁厚度t=7.0mm,满足要求
四、跨中截面管壁应力分析
1.计算参数:
末跨跨中管道中心计算水头H1=H-L/2×sinα
=56250-16000/2×sin44.0°=50693mm
伸缩节端部管道中心计算水头H'=H-L3×sinα
=56250-54000×sin44.0°=18738mm
伸缩节到跨中截面的计算长度L3'=L3-L/2=54000-16000/2=46000mm
2.荷载计算:
(1)径向内水压力
计算公式:
P=γw×H1
P=9.80×10-6×50693=0.497N/mm2
(2)钢管自重作用下垂直管轴方向的法向力
计算公式:
Qs=qs×L×cosα(每跨钢管自重)
qs=1.25πDtγs(单位长钢管自重,考虑加劲环等附件重量为钢管重量的25%)
qs=1.25×3.14×2000×7.0×7.85×10-5=4.316N/mm
Qs=4.316×16000×cos44.0°=49672N
(3)钢管中水重作用下垂直管轴方向的法向力
计算公式:
Qw=qw×L×cosα(每跨管内水重)
qw=0.25πD2γw(单位长管内水重)
qw=0.25×3.14×20002×9.80×10-6=30.788N/mm
Qw=30.788×16000×cos44.0°=354348N
(4)钢管自重作用下轴向分力
计算公式:
A1=qs×L3'×sinα
A1=4.316×46000×sin44.0°=137907N
(5)套筒式伸缩节端部的内水压力
计算公式:
A5=0.25π(D12-D22)H'γw
A5=0.25×3.14×(20202-20002)×18738×9.80×10-6=11596N
(6)温升时套筒式伸缩节止水填料的摩擦力
计算公式:
A6=π×D1×b1×μ1×γw
A6=3.14×2020×300×0.30×18738×9.80×10-6=104883N
(7)温升时支座对钢管的摩擦力
计算公式:
A7=n×(qs+qw)×L×f×cosα
A7=3×(4.316+30.788)×16000×0.10×cos44.0°=121206N
(8)轴向力的合力∑A
∑A=A1+A5+A6+A7
=137907+11596+104883+121206=375592N
3.跨中管壁截面应力计算公式:
(1)径向内水压力P在管壁中产生的环向应力σθ1:
σθ1=P×r/t×(1-r/H×cosα×cosθ)
式中:
r=D/2
θ为计算点径向与管中心铅垂线的夹角。
θ=0°为管顶点;θ=90°为管水平轴线处;θ=180°为管底
(2)轴向力合力∑A在横断面上产生的轴向应力σx1(拉力为正):
σx1=∑A/(2×π×r×t)
(3)法向力在横断面上产生的轴向应力σx2(拉力为正):
σx2=-M/(π×r2×t)×cosθ
式中:
M=(qs+qw)/10×L2×cosα
(4)内水压力P在管壁中产生的径向应力σr:
σr=-γw×(H1-r×cosα×cosθ)
4.跨中管壁截面各计算点应力复核条件:
σ=[σθ2+σx2+σr2-σθσx-σθσr-σxσr]1/2≤φ[σ]
式中:
σθ=σθ1
σx=σx1+σx2
相应计算工况的允许应力[σ]=0.55σs=0.55×235.0=129.3N/mm2
5.跨中管壁截面应力计算结果:
部位
σθ1
σx1
σx2
σx
σr
σ
φ[σ]
θ=0°
97.95
-11.96
-41.15
-53.11
-0.49
132.81
122.79
θ=90°
99.36
-11.96
-0.00
-11.96
-0.50
106.05
122.79
θ=180°
100.77
-11.96
41.15
29.20
-0.50
90.17
122.79
跨中管壁截面应力复核不满足要求!
五、加劲环及其旁管管壁应力分析
1.计算参数:
管壁计算厚度t=实际厚度-2=7-2=5mm
加劲环截面管道中心计算水头H2=H-l×sinα
=56250-4000×sin44.0°=53471mm
伸缩节端部管道中心计算水头H'=H-L3×sinα
=56250-54000×sin44.0°=18738mm
伸缩节到加劲环截面的计算长度L3'=L3-l=54000-16000=50000mm
2.荷载计算:
(1)径向内水压力
计算公式:
P=γw×H2
P=9.80×10-6×53471=0.524N/mm2
(2)钢管自重作用下垂直管轴方向的法向力
计算公式:
Qs=qs×L×cosα(每跨钢管自重)
qs=1.25πDtγs(单位长钢管自重,考虑加劲环等附件重量为钢管重量的25%)
qs=1.25×3.14×2000×7.0×7.85×10-5=4.316N/mm
Qs=4.316×16000×cos44.0°=49672N
(3)钢管中水重作用下垂直管轴方向的法向力
计算公式:
Qw=qw×L×cosα(每跨管内水重)
qw=0.25πD2γw(单位长管内水重)
qw=0.25×3.14×20002×9.80×10-6=30.788N/mm
Qw=30.788×16000×cos44.0°=354348N
(4)钢管自重作用下轴向分力
计算公式:
A1=qs×L3'×sinα
A1=4.316×50000×sin44.0°=149899N
(5)套筒式伸缩节端部的内水压力
计算公式:
A5=0.25π(D12-D22)H'γw
A5=0.25×3.14×(20202-20002)×18738×9.80×10-6=11596N
(6)温升时套筒式伸缩节止水填料的摩擦力
计算公式:
A6=π×D1×b1×μ1×γw
A6=3.14×2020×300×0.30×18738×9.80×10-6=104883N
(7)温升时支座对钢管的摩擦力
计算公式:
A7=n×(qs+qw)×L×f×cosα
A7=3×(4.316+30.788)×16000×0.10×cos44.0°=121206N
(8)轴向力的合力∑A
∑A=A1+A5+A6+A7
=149899+11596+104883+121206=387584N
3.加劲环截面几何参数计算:
(1)管壁等效翼缘宽(一侧)的倒数k
计算公式:
1/k=0.78×(r×t)1/2
1/k=0.78×(1000×5.0)1/2=55.2mm
k=0.0181/mm
(2)加劲环的净面积ARO
计算公式:
ARO=a×(h+t)
ARO=25×(100+5.0)=2625.0mm2
(3)加劲环的有效面积AR
计算公式:
AR=a×h+(a+2/k)×t
AR=25×100+(25+2/0.018)×5.0=3176.5mm2
(4)加劲环的有效截面重心轴至管中心距离rk
计算公式:
rk=[a×h×(h/2+t+r)+(2/k+a)×t×(r+t/2)]/AR
rk=[25×100×(100/2+5.0+1000)+(2/0.018+25)×5.0×(1000+5.0/2)]/3177=1044mm
(5)距离参数y1、y2
计算公式:
y1=h/2+t+r-rk
y2=rk-(r+t)
y1=100/2+5.0+1000-1043.8=11.2mm
y2=1043.8-(1000+5.0)=38.8mm
(6)加劲环有效截面惯性矩Jk
计算公式:
Jk=a×h3/12+a×h×y12+(2/k+a)×t3/12+(2/k+a)×t×(y2+t/2)2
Jk=25