自动控制原理实验报告球杆系统.docx
《自动控制原理实验报告球杆系统.docx》由会员分享,可在线阅读,更多相关《自动控制原理实验报告球杆系统.docx(23页珍藏版)》请在冰豆网上搜索。
自动控制原理实验报告球杆系统
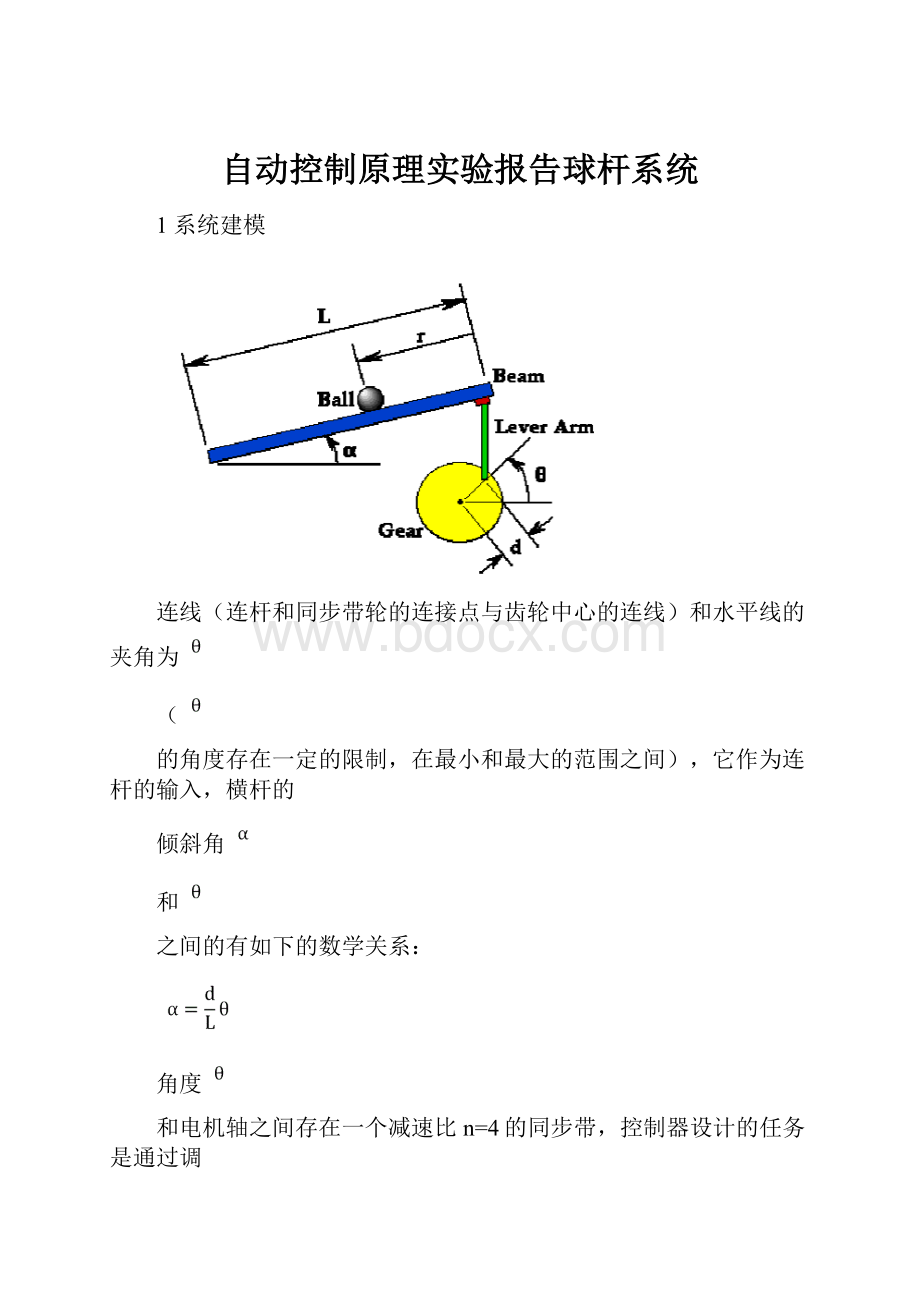
1系统建模
连线(连杆和同步带轮的连接点与齿轮中心的连线)和水平线的夹角为
(
的角度存在一定的限制,在最小和最大的范围之间),它作为连杆的输入,横杆的
倾斜角
和
之间的有如下的数学关系:
角度
和电机轴之间存在一个减速比n=4的同步带,控制器设计的任务是通过调
整齿轮的角度
,使得小球在某一位置平衡。
小球在横杆上滚动的加速度如下式:
其中:
小球在横杆上的位置r为输出
小球的质量m=0.11kg;
小球的半径R=0.015m;
重力加速度g=-9.8m/s2;
横杆长L=0.4m;
连杆和齿轮的连接点与齿轮中心的距离为d=0.04(m);
小球的转动惯量J=2*m*R^2/5(N/m2)。
我们假设小球在横杆上的运动为滚动,且摩擦力可以忽略不计。
因为我们期望角度
在0附近,因此我们可以在0附近对其进行线性化,得到近似的线性方程:
Laplace变换得:
2实验步骤
【主要方法】:
通过球杆系统仿真,与理想传递函数下的反馈系统的对比,深刻理解系统的调节以及稳定性特征。
2.1PID控制法
2.1.1P控制
1.含有控制器、球杆系统结构和小球位置反馈的系统框图如下所示:
其中,Xd(s)为小球目标位置的拉普拉斯变换,P控制器为:
GP(s)=KP
闭环系统的传递函数为:
其中,
。
2.MATLAB仿真
程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[-K];den=[100];
plant=tf(num,den);
kp=3;
sys_cl=feedback(kp*plant,1);
step(0.2*sys_cl)
(1)当Kp=3时
(2)当Kp=6时
(3)当Kp=10时
3.在Simulink环境下仿真
(1)当Kp=3时
(2)当Kp=6时
(3)当Kp=10时
分析:
从仿真图和实验图中可以看出,他们的大致波形是一致的,但由于实验受环境影响,如用手抓取小球,桌面收到碰撞震荡等,使波形出现很多毛刺,但系统是不稳定的,出现等幅振荡。
2.1.2PD控制
1.给控制器添加一个微分控制,闭环系统的结构图如下:
PD控制器的传递函数为:
为简单起见,我们假设固定比例增益KP,调整KD的大小。
闭环系统的传递函数为:
2.MATLAB仿真
程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[-K];den=[100];
plant=tf(num,den);
kp=6;
kd=6;
contr=tf([kdkp],1);
sys_cl=feedback(contr*plant,1);
t=0:
0.01:
5;
step(0.2*sys_cl)
(1)当Kp=6,Kd=6时
(2)当Kp=4,Kd=4时
3.在Simulink环境下仿真
(1)当Kp=6,Kd=6时
(2)当Kp=4,Kd=4时
分析:
可以看出,当控制器中加入一个微分控制时,闭环系统是一个稳定的系统。
当Kp=6,Kd=6时,超调量P.O.=20%,调节时间Ts=2.5s;当Kp=4,Kd=4时,超调量P.O.=13%,调节时间Ts=4.8s。
此时系统虽然是稳定的,但是超调量和调节时间都过大,稳定效果较差。
2.1.3PID控制
1.添加PID控制器后,闭环系统的结构图如下:
PID控制器的传递函数为:
其中,KD和KI对应于积分和微分控制,KP为比例增益.
闭环系统的传递函数如下所示:
2.MATLAB仿真
程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[-K];den=[100];
plant=tf(num,den);
kp=3;
kd=10;
ki=1;
contr=tf([kdkpki],1);
sys_cl=feedback(contr*plant,1);
t=0:
0.01:
100;
y=step(0.2*sys_cl,t);
plot(t,y),grid
(1)当Kp=10,Kd=10,Ki=1时
(2)当Kp=10,Kd=40,Ki=1时
(3)当Kp=15,Kd=40,Ki=0.5时
3.在Simulink环境下仿真
(1)当Kp=10,Kd=10,Ki=1时
(2)当Kp=10,Kd=40,Ki=1时
(3)当Kp=15,Kd=40,Ki=0.5时
分析:
可以看出,增大KD可以减少超调量,而减小调节时间可以增大Kp,第三个图明显的减少了系统的稳态误差,基本上满足了设计要求,但与MATLAB仿真相比,实际中系统会受到很多影响,因此总是有很多毛刺。
2.2根轨迹法
【主要方法】:
通过分析系统的开环零极点位置,来分析闭环系统的特性,通过增加极点或零点的方法(校正器),根轨迹以及闭环系统的响应都将发生改变。
1.添加控制器后,一个典型的闭环系统如下:
2.MATLAB仿真
(1)校正前程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[0.7];den=[100];
plant=tf(num,den);
sys_cl=feedback(plant,1);
t=0:
0.01:
50;
y=step(0.2*sys_cl,t);
plot(t,y),grid
校正前根轨迹
校正前单位阶跃响应
(2)校正后程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[K];
den=[100];
g0=tf(num,den);
sigma=10;%超调量(百分比)
ts=1;%调整时间
sigma=sigma/100;
zeta=sqrt(1/(pi^2/log(sigma)^2+1));%二阶系统参数ζ、ωn
wn=4/(ts*zeta);
s1_real=-wn*zeta;%Óɶþ½×ϵͳËã³öµÄ±Õ»·ÏµÍ³Ö÷µ¼¼«µã
s1_imag=wn*sqrt(1-zeta^2);
s1=s1_real+j*s1_imag;
phi=angle(s1);%由而写系统算出的闭环系统主导极点
num_s1=polyval(num,s1);
den_s1=polyval(den,s1);
g0_s1=num_s1/den_s1;%主导极点的相角
theta=angle(g0_s1);%未校正系统传递函数在主导极点上的相角θ
phi_c=pi-theta;%校正器的相角可由主导极点上闭环特征方程的相角条件确定
theta_z=(phi+phi_c)/2;
theta_p=(phi-phi_c)/2;
z_c=real(s1)-imag(s1)/tan(theta_z);%校正器零、极点
p_c=real(s1)-imag(s1)/tan(theta_p);
num_c=[1-z_c];
den_c=[1-p_c];
gc=tf(num_c,den_c)%校正器的传递函数
numc_s1=polyval(num_c,s1);
denc_s1=polyval(den_c,s1);
gc_s1=numc_s1/denc_s1;%校正器传递函数在主导极点上的值
K=1/(abs(g0_s1*gc_s1))%根据主导极点上闭环特征方程的幅值条件求增益
rlocus(g0*gc)%画根轨迹图
close=feedback(K*g0*gc,1);%闭环负反馈
figure
t=0:
0.01:
10;%时间标尺
step(close,t)%校正后系统单位阶跃响应
校正后根轨迹
校正后单位阶跃响应
3.在Simulink环境下仿真
(1)Zeros=[-2.4],Poles=[-13.80],Gain=[114.2]
(2)Zeros=[-0.5],Poles=[-4],Gain=[15.68]
(3)Zeros=[-0.5],Poles=[-5],Gain=[15.68]
分析:
由图可知,减小减小控制器的零、极点,会使系统的稳定性增加。
2.3频率响应法
【主要方法】根据开环传递函数的Bode图,给系统添加一个校正器,改变开环系统的Bode图,从而改变闭环系统的响应,使其达到期望的性能。
1.添加控制器后,一个典型的控制系统如下:
2.MATLAB仿真
(1)校正前程序代码
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K=(m*g*d)/(L*(J/R^2+m));
num=[K];den=[100];
g0=tf(num,den);
bode(g0)
uncomp=feedback(g0,1);
t=[0:
0.01:
100];
y=step(uncomp,t);
plot(t,y),grid
校正前Bode图
校正前单位阶跃响应
(2)校正后程序代码:
m=0.11;R=0.015;g=-9.8;L=0.4;d=0.04;
J=2*m*R^2/5;
K0=(m*g*d)/(L*(J/R^2+m));
num=[0.7];den=[100];
g0=tf(num,den);
sigma=10;%超调量(百分比)
sigma=sigma/100;
zeta=sqrt(1/(pi^2/log(sigma)^2+1));%二阶系统阻尼比ζ
gamma=atan(2/sqrt(sqrt(1/zeta^4+4)-2));%相角裕度
phi=gamma;%相位超前角
%wc=1
wc1=1%频率带宽的中心频率
a1=(1-sin(phi))/(1+sin(phi));%·分度系数
T1=1/(wc1*sqrt(a1));%时间常数
numlead1=[T11];%校正系统传递函数
denlead1=[a1*T11];
gc1=tf(numlead1,denlead1);
K=2;
sys1=series(K*g0,gc1);
sys_cl1=feedback(sys1,[1]);
%wc=2
wc2=2;
a2=(1-sin(phi))/(1+sin(phi));
T2=1/(wc2*sqrt(a2));
numlead2=[T21];
denlead2=[a2*T21];
gc2=tf(numlead2,denlead2);
K=2;
sys2=series(K*g0,gc2);
sys_cl2=feedback(sys2,[1]);
%wc=3
wc3=3;
a3=(1-sin(phi))/(1+sin(phi));
T3=1/(wc3*sqrt(a3));
numlead3=[T31];
denlead3=[a3*T31];
gc3=tf(numlead3,denlead3);
K=2;
sys3=series(K*g0,gc3);
sys_cl3=feedback(sys3,[1]);
bode(sys1,sys2,sys3),grid
t=[0:
0.01:
20];
y1=step(sys_cl1,t);
y2=step(sys_cl2,t);
y3=step(sys_cl3,t);
plot(t,y1,t,y2,t,y3),grid
校正后bode图
校正后单位阶跃响应
1.在Simulink环境下仿真
(1)Numerator=130*[16.71],Denominator=[7.61]
(2)Numerator=3*[4.41],Denominator=[0.221]
(3)Numerator=4*[2.21],Denominator=[0.111]
分析:
减小增益值可以抑制超调量,从而增加系统的稳定性。
3实验心得总结
通过这次球杆实验使我对控制系统有了更深刻更直观的认识,了解到控制系统在实际生活特别是自动化生产中有着重要的作用。
日常生活中的水温控制,驾驶系统,以至于点点滴滴都会应用到反馈系统的理论。
一个控制系统往往会有很多的控制器设计方法,PID控制法、根轨迹法、频率响应法等。
在实验中,不管用什么方法都需要反复尝试不同的控制参数,直到得到满意的控制效果。
本实验也让我对PID控制的认识有了深化,但PID的调节过程比较繁琐,需要不断的尝试各种参数,发现其中规律,并最终寻找到最合适的系统参数。
在实验中,发现图像中存在很多瑕疵,可见系统总要受到外界环境的影响,在实际系统的设计中,有时候需要考虑各种外界干扰的存在,尽可能减少它们的作用。
另外要提到的是,实验设备对实验结果的影响是很大的,在实验中我们组的simulink仿真图像毛刺特别多,系统特别不稳定,但是经过我们反复修改参数和尝试,终于使系统的稳定性提高了一点点。
所以希望学校能更新一下部分实验设备,以方便我们今后的学习与实践。