摆线公式等.docx

摆线公式等.docx

《摆线公式等.docx》由会员分享，可在线阅读，更多相关《摆线公式等.docx（11页珍藏版）》请在冰豆网上搜索。

摆线公式等

摆线公式等

摆线方程

它是这样定义的：

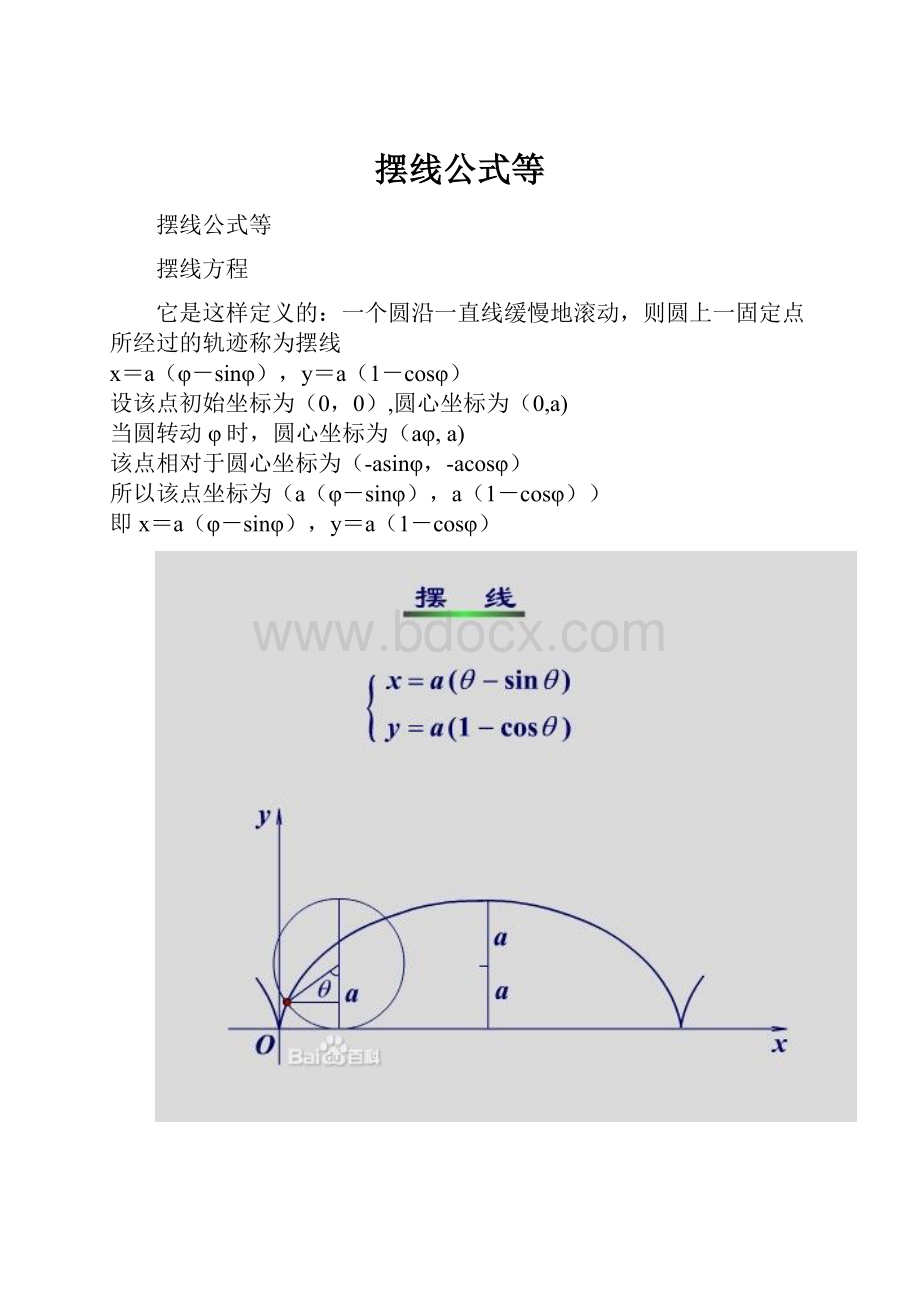
一个圆沿一直线缓慢地滚动，则圆上一固定点所经过的轨迹称为摆线

x＝a（φ－sinφ），y＝a（1－cosφ）

设该点初始坐标为（0，0）,圆心坐标为（0,a）

当圆转动φ时，圆心坐标为（aφ,a）

该点相对于圆心坐标为（-asinφ，-acosφ）

所以该点坐标为（a（φ－sinφ），a（1－cosφ））

即x＝a（φ－sinφ），y＝a（1－cosφ）

摆线[编辑]

维基百科，自由的百科全书

本条目需要扩充。

（2010年7月25日） 

请协助改善这篇条目，更进一步的信息可能会在讨论页或扩充请求中找到。

请在扩充条目后将此模板移除。

一条由滚动的圆所生成的摆线

在数学中，摆线 （Cycloid）被定义为，一个圆沿一条直线运动时，圆边界上一定点所形成的轨迹。

它是roulette曲线的一个例子。

摆线也是最速降线问题和等时降落问题的解。

  [隐藏] 

∙1 历史

∙2 方程

∙3 面积

∙4 弧长

∙5 其它相关联的曲线

∙6 应用

∙7 参考

∙8 外部连结

历史[编辑]

摆线的研究最初开始于NicholasofCusa，之后梅森（MarinMersenne） 也有针对摆线的研究。

1599年伽利略为摆线命名。

1634年G.P.deRoberval指出摆线下方的面积是生成它的圆面积的三倍。

1658年克里斯多佛·雷恩也向人们指出摆线的长度是生成它的圆直径的四倍。

在这一时期，伴随着许多发现，也出现了众多有关发现权的争议，甚至抹杀他人工作的现象，而因此摆线也被人们称作“几何学中的海伦”（TheHelenofGeometers）。

[1].

方程[编辑]

由半径为2的圆所生成的摆线

过原点半径为r的摆线参数方程为

在这里实参数t是在弧度之下，圆滚动的角度。

对每一个给出的t，圆心的坐标为（rt,r）。

通过替换解出t可以求的笛卡尔坐标方程为

摆线的第一道拱由参数t在（0,2π）区间内的点组成。

摆线也满足下面的微分方程。

面积[编辑]

一条由半径为r的圆所生成的拱形面积可以由下面的参数方程界定：

微分，

于是可以求得

弧长[编辑]

弧形的长度可以由下面的式子计算出：

其它相关联的曲线[编辑]

一些曲线同摆线紧密相关。

当我们弱化定点只能固定在圆边界上时，我们得到了短摆线（curtatecycloid）和长摆线（prolatecycloid），两者合称为次摆线（trochoid），前面的情形是定点在圆的内部，后者则是在圆外。

trochoid则是上述三种曲线的统称。

更进一步，如果我们让圆也沿着一个圆滚动而不是直线的话，我们会得到 外摆线（epicycloid） （沿着圆的外部运动，定点在圆的边缘），内摆线（hypocycloid）（沿着圆内部滚动，定点在圆的边缘）以及外旋轮线（epitrochoid）和内旋轮线（hypotrochoid）（定点可以在圆内的任一点包括边界。

）

小圆边缘沿大圆转动：

圆外螺线/外摆线 · 圆内螺线/内摆线

小圆短径外转：

外旋轮线 · 小圆长径内转：

内旋轮线

小圆边缘沿直线转动：

摆线

外摆线[编辑]

维基百科，自由的百科全书

不同的外摆线

外摆线 是所有形式为

的曲线，其中 n 为正实数。

轨迹定义[编辑]

n=4的外摆线轨迹

假设有一个定圆，若有另一个半径是刚才的圆形的

倍的圆在上滚动，则圆周上的一定点在滚动时划出的轨迹就是一条外摆线。

心脏线[编辑]

心脏线

心脏线是外摆线的一种，其 n 为2。

它亦可以极坐标的形式表示：

r =1+cos θ

这样的心脏线的周界为8，围得的面积为

。

心脏线亦为蚶线的一种。

在 曼德博集合 正中间的图形便是一个心脏线。

心脏线的英文名称“Cardioid”是deCastillon在 1741年 的《PhilosophicalTransactionsoftheRoyalSociety》发表的；意为“像心脏的”。

肾脏线[编辑]

肾脏线亦是外摆线的一种，其 n 为3。

圆内螺线[编辑]

维基百科，自由的百科全书

内摆线（圆内螺线）是所有形式为

的曲线，其中 n 为正实数。

轨迹定义[编辑]

假设有一个定圆，若有另一个半径是刚才的圆形的

倍的圆在其内部滚动，则圆周上的一定点在滚动时划出的轨迹就是一条内摆线（圆内螺线）。

三尖瓣线和星形线[编辑]

三尖瓣线（Deltoid，字自“Delta”Δ）是内摆线（圆内螺线）一种，其 n 为2（或1/2）。

[1]

星形线是内摆线（圆内螺线）一种，其 n 为3。

外旋轮线[编辑]

维基百科，自由的百科全书

R =3, r =1和 d =1/2的外旋轮线

外旋轮线（Epitrochoid - IPA [ɛpɪˈtrɒkɔɪd,-ˈtrəʊ-]）是追踪附着在围绕半径为 R 的固定的圆外侧滚转的半径 r 的圆上的一个点而得到的转迹线，这个点距离外部滚动的圆的中心的距离是 d。

外旋轮线的参数方程是

特殊情况包括 R=r 的蜗牛线和 d=r 的外摆线。

经典的玩具万花尺追踪外旋轮线和内旋轮线。

转子活塞发动机的定子是外旋轮线。

内旋轮线[编辑]

维基百科，自由的百科全书

红色曲线是 R =5.0, r =3, d =5的内旋轮线

内旋轮线（hypotrochoid）是追踪附着在围绕半径为 R 的固定的圆内侧滚转的半径为 r 的圆上的一个点得到的转迹线，这个点到内部滚动的圆的中心的距离是 d。

内旋轮线的参数方程是:

特殊情况包括 d = r 的内摆线和 R =2r 的椭圆。

经典的玩具万花尺追踪出内旋轮线和外旋轮线。