实验08光纤位移传感器特性实验的数据处理实验报告.docx
《实验08光纤位移传感器特性实验的数据处理实验报告.docx》由会员分享,可在线阅读,更多相关《实验08光纤位移传感器特性实验的数据处理实验报告.docx(11页珍藏版)》请在冰豆网上搜索。
实验08光纤位移传感器特性实验的数据处理实验报告
实验报告:
实验08(光纤位移传感器特性实验的数据处理)实验报告
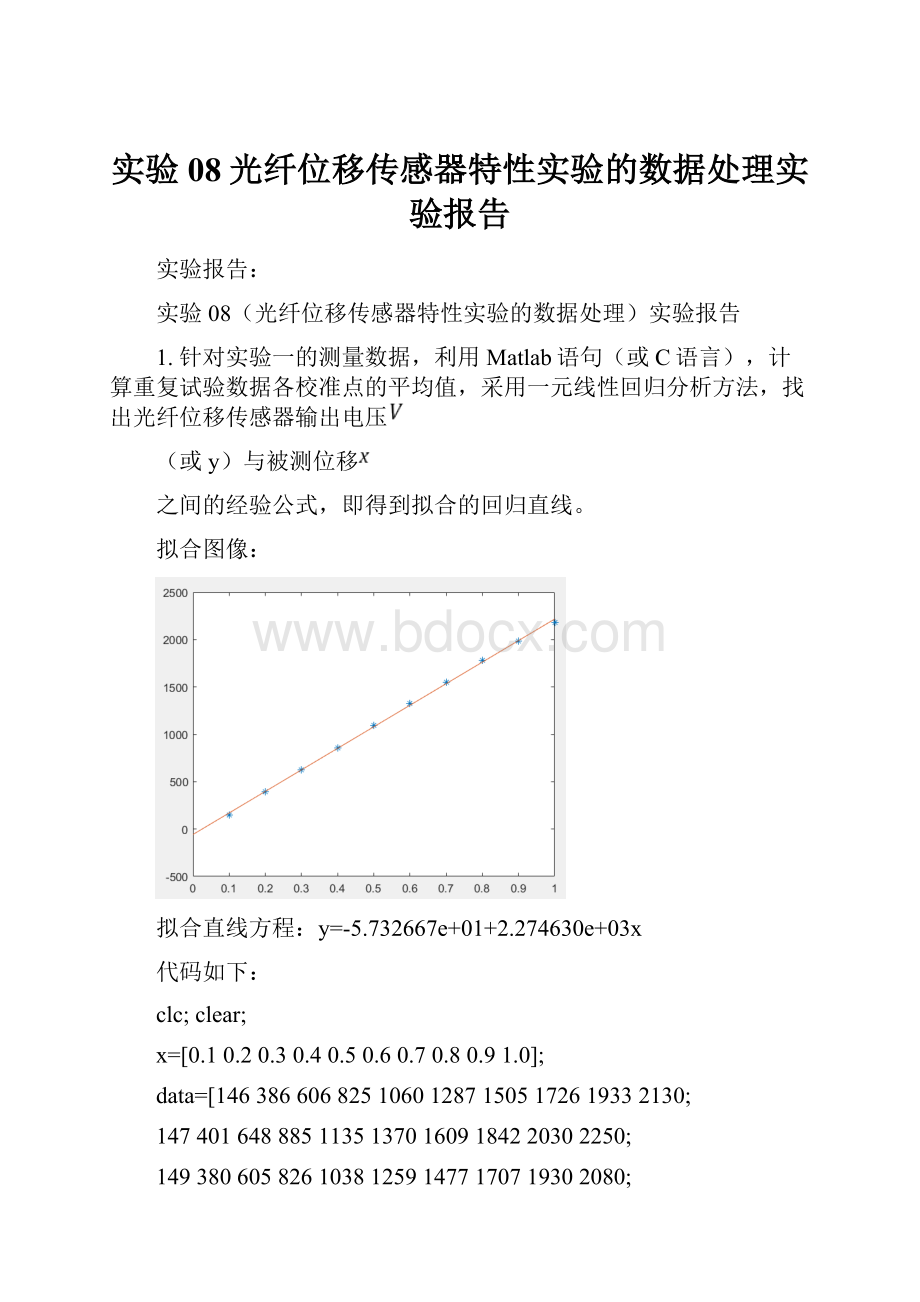
1.针对实验一的测量数据,利用Matlab语句(或C语言),计算重复试验数据各校准点的平均值,采用一元线性回归分析方法,找出光纤位移传感器输出电压
(或y)与被测位移
之间的经验公式,即得到拟合的回归直线。
拟合图像:
拟合直线方程:
y=-5.732667e+01+2.274630e+03x
代码如下:
clc;clear;
x=[0.10.20.30.40.50.60.70.80.91.0];
data=[146386606825106012871505172619332130;
147401648885113513701609184220302250;
149380605826103812591477170719302080;
149400644874112313571599182720202220;
150384605831106012891490172919442130;
146408651885113913761605183120302250;
149373592831105212891496173019392120;
141402644878113013621603183320202250;
153389609838108313071510173619472140;
143401642889113713701606184020302250];%测量数据
Each_Point_Average_Value=mean(data,1,'native');%每个点的测量数据的算术平均值
N=length(Each_Point_Average_Value);%数据个数
%数据处理第一题
fprintf('\n计算回归方程并作图拟合\n');
%以下以xt指代x,yt指代Each_Point_Average_Value
t1=0;%计算xtyt乘积和,最后乘以N
fori=1:
N;
t1=t1+Each_Point_Average_Value(i)*x(i);
end
t1=t1*N;
t2=0;%计算xt的和
fori=1:
N;
t2=t2+x(i);
end
t3=0;%计算yt的和
fori=1:
N;
t3=t3+Each_Point_Average_Value(i);
end
t4=0;%计算xt的平方和再乘以N
fori=1:
N;
t4=t4+x(i)^2;
end
t4=t4*N;
t5=0;%计算xt的总和的平方
t5=t2^2;
t6=t4/N;
t7=t3;
t8=t2;
t9=t1/N;
t10=t4;
t11=t5;
%计算b的回归值
b=(t1-t2*t3)/(t4-t5);
%计算b0的回归值
b0=(t6*t7-t8*t9)/(t10-t11);
%作数据分布图和回归曲线
X=x;
Y1=Each_Point_Average_Value;
fprintf('回归方程:
y=%d+%dx\n',b0,b);
fprintf('以下作图\n');
x_t=[00.10.20.30.40.50.60.70.80.91.0];
Y2=b0+b*x_t;
plot(X,Y1,'*',x_t,Y2)
2.利用Matlab语句(或C语言),对所得到的一元线性回归方程进行方差分析,列出方差分析表;
分析表如下所示:
代码如下:
%数据处理第二题和第三题:
对回归方程进行方差分析和显著性检验
fprintf('\n对回归方程进行显著性检验\n');
Size_data=size(data);%计算data矩阵的规格
%Size_data
(1)为矩阵行数{m次测量},Size_data
(2)矩阵列数{N个点的测量}
%以下分别计算lxx,lxy,lyy
%计算lxx
lxx=0;
t1=0;
fori=1:
length(x);
t1=t1+x(i)^2;
end
t2=0;
fori=1:
length(x);
t2=t2+x(i);
end
t2=t2^2;
lxx=t1-t2/length(x);
%计算lxy
lxy=0;
t1=0;
t2=0;
t3=0;
fori=1:
length(x);
t1=t1+x(i)*Each_Point_Average_Value(i);
end
t2=0;
fori=1:
length(x);
t2=t2+x(i);
end
t3=0;
fori=1:
length(Each_Point_Average_Value);
t3=t3+Each_Point_Average_Value(i);
end
lxy=t1-(t2*t3)/length(x);
%计算lyy
lyy=0;
t1=0;
fori=1:
length(Each_Point_Average_Value);
t1=t1+Each_Point_Average_Value(i)^2;
end
t2=0;
fori=1:
length(Each_Point_Average_Value);
t2=t2+Each_Point_Average_Value(i);
end
t2=t2^2;
lyy=t1-t2/length(Each_Point_Average_Value);
%Size_data
(1)为矩阵行数{m次测量},Size_data
(2)矩阵列数{N个点的测量}
%计算回归平方和U和对应的自由度Vu及其对应的方差r_U
U=0;
U=Size_data
(1)*(lxy/lxx)*lxy;
Vu=1;
r_U=U/Vu;
%计算失拟平方和QL和对应的自由度Vql及其对应的方差r_QL
QL=0;
QL=Size_data
(1)*lyy-U;
Vql=Size_data
(2)-2;
r_QL=QL/Vql;
%计算误差平方和QE和对应的自由度Vqe及其对应的方差r_QE
QE=0;
QE1=0;
fori=1:
Size_data
(2)%N
QE=QE+QE1;
forj=1:
Size_data
(1)%m
QE1=(data(j,i)-Each_Point_Average_Value(i))^2;
end
end
QE;
Vqe=Size_data
(2)*(Size_data
(1)-1);
r_QE=QE/Vqe;
%合成的总的离差平方和S及其对应的自由度Vs
S=U+QE+QL;
Vs=Vu+Vqe+Vql;
F_example=6.84;
F1_example=2.70;
F=(U/Vu)/(QE/Vqe);
F1=(QL/Vql)/(QE/Vqe);
F2=(U/Vu)/((QL+QE)/(Vql+Vqe));
%%%%%%%%%%%%以下开始制作方差分析表%%%%%%%%%%%%%%
data_excel=cell(5,6);
title={'来源','平方和','自由度','方差','F','显著性'};%列表头
excel_A={'回归','失拟','误差','总计'};
excel_B=[U;QL;QE;S];%平方和数据
excel_C=[Vu;Vql;Vqe;Vs];%自由度数据
excel_D=[r_U;r_QL;r_QE];%方差数据
excel_E=[F;F1];%F检验数据
excel_F=[F_example;F1_example];%显著性参考值
excel_G=['-'];
%格式调整
excel_B=num2cell(excel_B,3);
excel_C=num2cell(excel_C,3);
excel_D=num2cell(excel_D,3);
excel_E=num2cell(excel_E,3);
excel_F=num2cell(excel_F,3);
excel_G=num2cell(excel_G,3);
%整合数据
data_excel(1,1:
end)=title;
data_excel(2:
end,1)=excel_A;
data_excel(2:
end,2)=excel_B;
data_excel(2:
end,3)=excel_C;
data_excel(2:
4,4)=excel_D;
data_excel(2:
3,5)=excel_E;
data_excel(2:
3,6)=excel_F;
data_excel(5,4)=excel_G;
data_excel(4:
end,5)=excel_G;
data_excel(4:
end,6)=excel_G;
xlswrite('data_excel.xls',data_excel);%写入表格
data_excel
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
3.利用Matlab语句(或C语言),对回归方程进行显著性检验,确定回归方程拟合的好坏,分析光纤位移传感器的误差。
%对结果进行F检验显著度取0.01
F_example=6.84;
F1_example=2.70;
F=(U/Vu)/(QE/Vqe);
F1=(QL/Vql)/(QE/Vqe);
F2=(U/Vu)/((QL+QE)/(Vql+Vqe));
fprintf('以下为F检验值\n');
fprintf('F=%d\n',F);
fprintf('对失拟平方和进行F检验:
\nF1=%d\n',F1);
fprintf('对失拟平方和以及误差平方和合并进行F检验:
\nF2=%d\n',F2);
%F显著,F1不显著,F2显著
%结论:
非线性误差很小,一元回归方程在显著度为0.01的水平上拟合的很好
fprintf('F显著,F1不显著,F2显著\n结论:
非线性误差很小,一元回归方程在显著度为0.01的水平上拟合的很好\n');
运行结果:
分析误差:
拟合直线方程:
y=-5.732667e+01+2.274630e+03x
拟合图像:
由上述拟合图像和拟合直线方程可得,该光纤位移传感器存在系统误差,在零点处出现了偏移,偏移量为-57.32667mm。
该光纤位移传感器不存在粗大误差。
4.画出程序流程图。