初二等腰三角形培优学案同步讲义.docx

初二等腰三角形培优学案同步讲义.docx

《初二等腰三角形培优学案同步讲义.docx》由会员分享，可在线阅读，更多相关《初二等腰三角形培优学案同步讲义.docx（12页珍藏版）》请在冰豆网上搜索。

初二等腰三角形培优学案同步讲义

学科教师辅导讲义

学员编号：

年级：

八年级（下）

课时数：

3

学员姓名：

辅导科目：

数学

学科教师：

授课主题

第01讲-等腰三角形

授课类型

T同步课堂

P实战演练

S归纳总结

教学目标

1掌握等腰三角形、等边三角形的性质、判定定理；

2掌握含30°角的直角三角形的性质定理及其证明；

3能够用综合法证明等腰三角形的有关性质及其判定定理。

授课日期及时段

T（Textbook-Based）——同步课堂

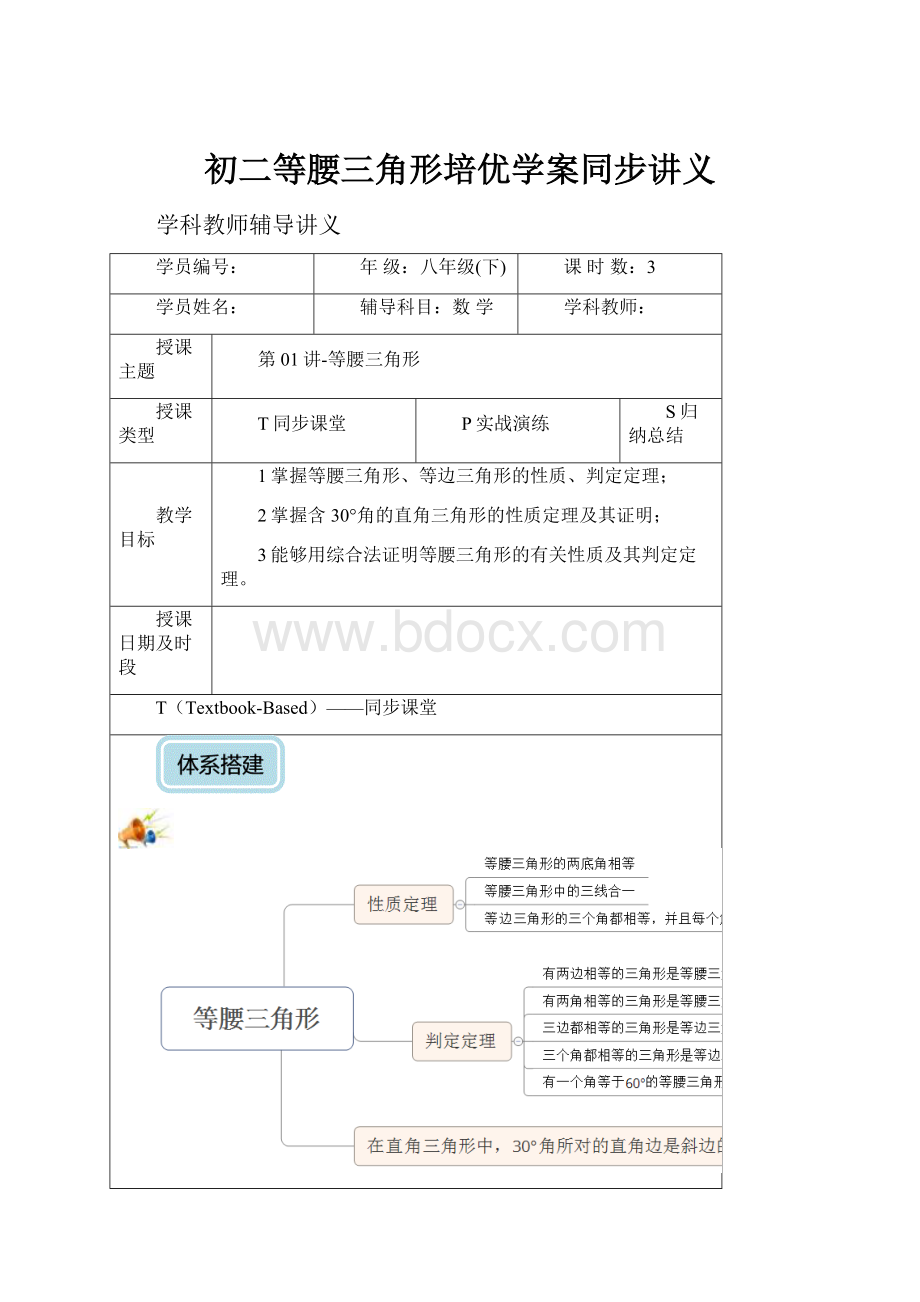
一、知识梳理

1、等腰三角形的性质定理

（1）两角分别相等且其中一组等角的对边相等的两个三角形全等。

（AAS）

（2）等腰三角形的两底角相等。

即等边对等角。

（3）推论：

等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。

即三线合一。

（4）等边三角形的三个内角都相等，并且每个角都等于60°。

2、等腰三角形的判定定理

（1）有两条边相等的三角形是等腰三角形。

（2）有两个角相等的三角形是等腰三角形。

即等角对等边。

（3）三个角都相等的三角形是等边三角形。

（4）有一个角等于60°的等腰三角形是等边三角形。

3、在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。

4、反证法：

先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果，从而证明命题的结论一定成立。

考点一：

等腰三角形的性质

例1、一个等腰三角形的两边长分别为4，8，则它的周长为（　　）

A．12B．16

C．20D．16或20

例2、如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）

A．15°B．17.5°

C．20°D．22.5°

例3、一个三角形可被剖成两个等腰三角形，原三角形的一个内角为36度，

求原三角形最大内角的所有可能值．

例4、如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3=A2D；…，按此做法进行下去，∠An的度数为　　．

例5、如图1，Rt△ABC中AB=AC，点D、E是线段AC上两动点，且AD=EC，AM垂直BD，垂足为M，AM的延长线交BC于点N，直线BD与直线NE相交于点F．试判断△DEF的形状，并加以证明．

说明：

（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；

（2）在你经历说明

（1）的过程之后，可以从下列①、②中选取一个补充或者更换已知条件，完成你的证明．

1、画出将△BAD沿BA方向平移BA长，然后顺时针旋转90°后图形；

2、点K在线段BD上，且四边形AKNC为等腰梯形（AC∥KN，如图2）．

附加题：

如图3，若点D、E是直线AC上两动点，其他条件不变，试判断△DEF的形状，并说明理由．

考点二：

等腰三角形的判定

例1、△ABC的三边长a，b，c满足关系式（a﹣b）（b﹣c）（c﹣a）=0，则这个三角形一定是（　　）

A．等腰三角形B．等边三角形

C．等腰直角三角形D．无法确定

例2、如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）

A．5个B．4个

C．3个D．2个

例3、如图，△ABC中，BF、CF分别平分∠ABC和∠ACB，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：

①△BDF和△CEF都是等腰三角形；

②∠DFB=∠EFC；

③△ADE的周长等于AB与AC的和；

④BF=CF．

其中正确的是　　．（填序号，错选、漏选不得分）

例4、如图，以△ABC的边AB、AC为直角边向外作等腰直角△ABE和△ACD，M是BC的中点，请你探究线段DE与AM之间的关系．

说明：

（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；

（2）在你经历说明

（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．①画出将△ACM绕某一点顺时针旋转180°后的图形；

②∠BAC=90°（如图）

附加题：

如图，若以△ABC的边AB、AC为直角边，向内作等腰直角△ABE和△ACD，其它条件不变，试探究线段DE与AM之间的关系．

P（Practice-Oriented）——实战演练

Ø课堂狙击

1、等腰三角形的两边长分别为4cm和8cm，则它的周长为（　　）

A．16cmB．17cm

C．20cmD．16cm或20cm

2、如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=70°，则∠BAC的大小为（　　）

A．40°B．30°

C．70°D．50°

3、如图，∠B=∠C，∠1=∠3，则∠1与∠2之间的关系是（　　）

A．∠1=2∠2B．3∠1﹣∠2=180°

C．∠1+3∠2=180°D．2∠1+∠2=180°

4、如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列四个条件：

①∠EBO=∠DCO；②BE=CD；③OB=OC；④OE=OD．从上述四个条件中，选取两个条件，不能判定△ABC是等腰三角形的是（　　）

A．①②B．①③C．③④D．②③

5、如图，在△ABC中AB=AC，∠A=36°，BD平分∠ABC，则∠1=　　度，图中有　个等腰三角形．

6、如图，AD是直角三角形△ABC斜边上的中线，把ADC沿AD对折，点C落在点C′处，连接CC′，则图中共有等腰三角形　　个．

7、如图1，是我们平时使用的等臂圆规，即CA=CB．若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示，其张角度数变化如下：

∠A1C1A2=160°，∠A2C2A3=80°，∠A3C3A4=40°，∠A4C4A5=20°，…．，根据上述规律请你写出∠An+1AnCn=　　°．（用含n的代数式表示）

8、如图，在△ABC中，AB=AC，点D是BC边上的中点，DE、DF分别垂直AB、AC于点E和F．

求证：

DE=DF．

9、如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F．

求证：

△ABC是等腰三角形．

Ø课后反击

1、已知等腰三角形的一个底角的度数为70°，则另外两个内角的度数分别是（　　）

A．55°，55°B．70°，40°

C．55°，55°或70°，40°D．以上都不对

2、等腰三角形顶角是84°，则一腰上的高与底边所成的角的度数是（　　）

A．42°B．60°

C．36°D．46°

3、如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（　　）

A．44°B．66°

C．88°D．92°

4、如图，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ABC=β．若α=10°，则β的度数是（　　）

A．40°B．50°

C．60°D．不能确定

5、如图，在△ABC，∠A=36°，∠B=72°，AC的垂直平分线分别交AC、AB于点D，E，则图中等腰三角形的个数为（　　）

A．2个B．3个

C．4个D．5个

6、如图，△ABC中，AB=AC，AD是∠BAC的平分线，若△ABD的周长为12，△ABC的周长为16，则AD的长为　　．

7、如图，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O．给出下列三个条件：

①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出一种情形）：

　．

8、

如图，∠BAC=θ（0°＜θ＜90°），现只用4根等长的小棒将∠BAC固定，从点A1开始依次向右摆放，其中A1A2为第1根小棒，且A1A2=AA1，则角θ的取值范围是　．

9、数学课上，同学们探究下面命题的正确性：

顶角为36°的等腰三角形具有一种特性，即经过它某一顶点的一条直线可把它分成两个小等腰三角形．为此，请你解答问题

（1）．

（1）已知：

如图①，在△ABC中，AB=AC，∠A=36°，直线BD平分∠ABC交AC于点D．求证：

△ABD与△DBC都是等腰三角形；

（2）在证明了该命题后，小乔发现：

下面两个等腰三角形如图②、③也具有这种特性．请你在图②、图③中分别画出一条直线，把它们分成两个小等腰三角形，并在图中标出所有等腰三角形两个底角的度数；

（3）接着，小乔又发现：

其它一些非等腰三角形也具有这样的特性，即过它其中一个顶点画一条直线可以将原三角形分成两个小等腰三角形．请你画出两个不同类型且具有这种特性的三角形的示意图，并在图中标出可能的各内角的度数．（说明：

要求画出的两个三角形不相似，且不是等腰三角形．）

（4）请你写出两个符合（3）中一般规律的非等腰三角形的特征．

1、【2015•长沙】下列条件中，不能判定△ABC是等腰三角形的是（　　）

A．a=3，b=3，c=4B．a：

b：

c=2：

3：

4

C．∠B=50°，∠C=80°D．∠A：

∠B：

∠C=1：

1：

2

2、【2016•山东】如下图中，将△ABC沿BD对折，使得点C落在AB上的点C′处，且∠C=2∠CBD，已知∠A=36°．

（1）求∠BDC的度数；

（2）写出图中所有的等腰三角形（不用证明）

S（Summary-Embedded）——归纳总结

1、等腰三角形的性质定理

（1）两角分别相等且其中一组等角的对边相等的两个三角形全等。

（AAS）

（2）等腰三角形的两底角相等。

即等边对等角。

（3）推论：

等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。

即三线合一。

（4）等边三角形的三个内角都相等，并且每个角都等于60°。

2、等腰三角形的判定定理

（1）有两条边相等的三角形是等腰三角形。

（2）有两个角相等的三角形是等腰三角形。

即等角对等边。

（3）三个角都相等的三角形是等边三角形。

（4）有一个角等于60°的等腰三角形是等边三角形。

1、涉及等腰三角形腰上的高的问题时，需要注意分类讨论；

2、等腰三角形“三线合一”的成立的条件一定要明确；

3、等腰三角形需要满足一般三角形的性质。

Ø本节课我学到

Ø我需要努力的地方是