压轴题选2.docx

压轴题选2.docx

《压轴题选2.docx》由会员分享，可在线阅读，更多相关《压轴题选2.docx（11页珍藏版）》请在冰豆网上搜索。

压轴题选2

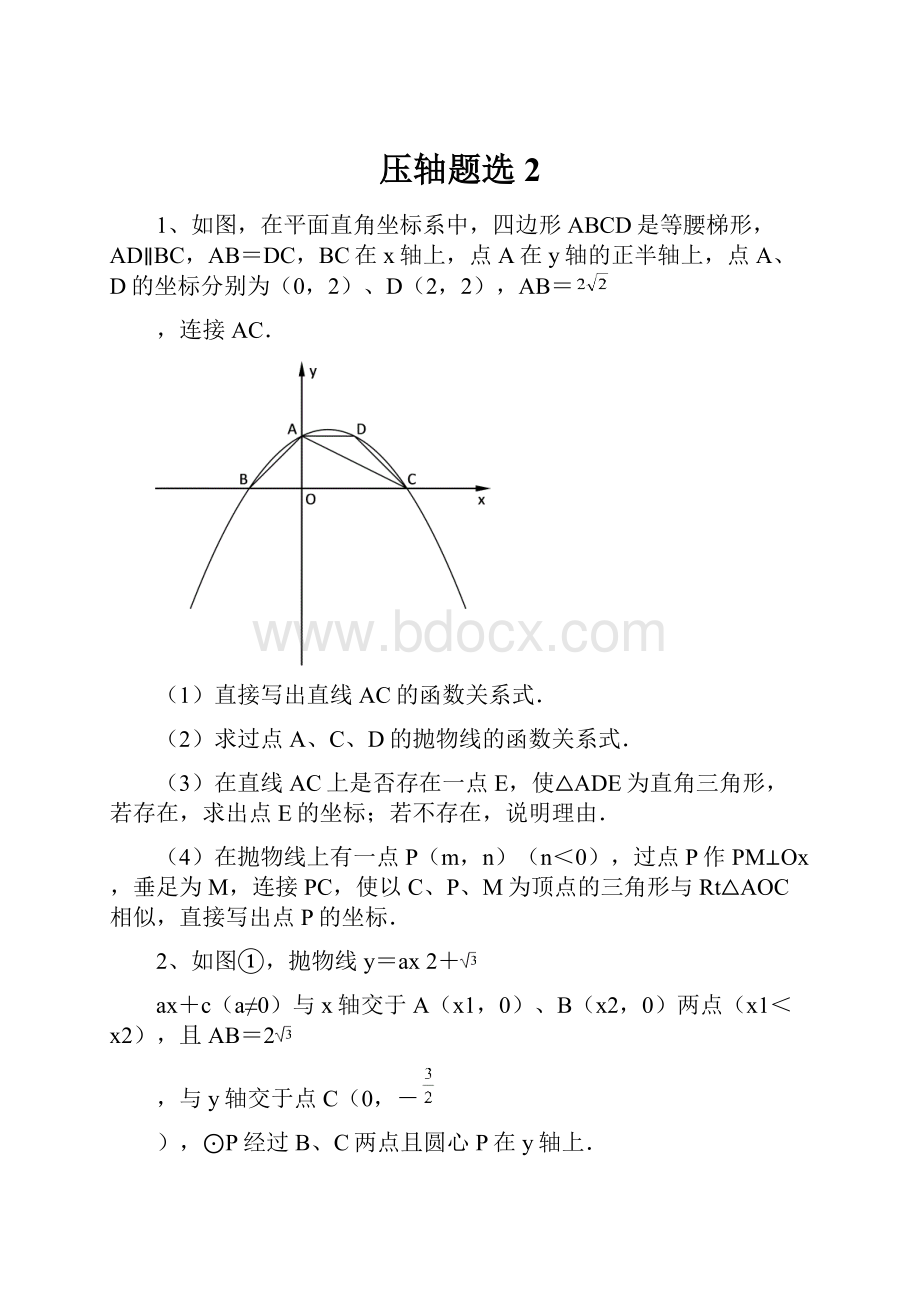
1、如图，在平面直角坐标系中，四边形ABCD是等腰梯形，AD∥BC，AB＝DC，BC在x轴上，点A在y轴的正半轴上，点A、D的坐标分别为（0，2）、D（2，2），AB＝

，连接AC．

（1）直接写出直线AC的函数关系式．

（2）求过点A、C、D的抛物线的函数关系式．

（3）在直线AC上是否存在一点E，使△ADE为直角三角形，若存在，求出点E的坐标；若不存在，说明理由．

（4）在抛物线上有一点P（m，n）（n＜0），过点P作PM⊥Ox，垂足为M，连接PC，使以C、P、M为顶点的三角形与Rt△AOC相似，直接写出点P的坐标．

2、如图①，抛物线y＝ax2＋

ax＋c（a≠0）与x轴交于A（x1，0）、B（x2，0）两点（x1＜x2），且AB＝2

，与y轴交于点C（0，－

），⊙P经过B、C两点且圆心P在y轴上．

（1）求抛物线的解析式；

（2）连接BP并延长交⊙P于点D，交抛物线于点E．

ⅰ）求证：

点D在抛物线的对称轴上；点C，E关于抛物线的对称轴对称；

ⅱ）求经过点D的⊙P的切线的解析式．

3、如图，在△ABC中，AD平分∠BAC交BC于点D，，以C为圆心，CD为半径作⊙C，交BC的延长线于点E，交AD于点F，交AE于点G，且∠CAE＝∠B，DF:

EF＝3:

4．

（1）求证：

D是BE的中点；

（2）求cos∠AEB的值；

（3）若DF＝4，求△ABC的面积．

4、已知：

如图，在△ABC中，∠A＝45°．以AB为直径的⊙O交AC于点D，且AD＝DC，CO的延长线交⊙O于点E，过点E作弦EF⊥AB，垂足为点G．

（1）求证：

BC是⊙O的切线；

（2）求sin∠ACO的值；

（3）若AB＝2，求EF的长．

5、如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21．动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．

（1）设△BPQ的面积为S，求S与t之间的函数关系式；

（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

（3）当线段PQ与线段AB相交于点O，且2AO＝OB时，求∠BQP的正切值；

（4）是否存在时刻t，使得PQ⊥BD？

若存在，求出t的值；若不存在，请说明理由．

6、如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD＝10，连接BD．

（1）求证：

∠CDE＝2∠B；

（2）若BD:

AB＝

:

2，求⊙O的半径及DF的长．

7、如图，点A、B坐标分别为（8，0）、（0，6），点C是线段AB的中点，点P是射线BA上一动点，过P作PD⊥y轴于D，饱PE⊥x轴于E．设OE＝t，矩形OEPD与△POC重合部分的面积为S．

（1）求线段OC所在直线的解析式；

（2）求S与t的函数关系式；

（3）当点P在线段AB上时，求S的最大值；

（4）若S＝2，则t的值有_________个．

8、如图，直线y＝－

x＋

与x轴、y轴分别交于A、B两点，⊙M经过原点O及A、B两点，C是⊙M上一点，连结BC交OA于点D．

（1）若∠COD＝∠CBO，求点C的坐标；

（2）延长BC到P，使DP＝BD，连结AP，判断直线PA与⊙M的位置关系，并说明理由．

9、如图，矩形OABC在平面直角坐标系中，若OA、OC的长满足|OA－2|＋（OC－

）2＝0．

（1）求B、C两点的坐标．

（2）把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求直线BB′的解析式．

（3）在直线BB′上是否存在点P，使△ADP为直角三角形？

若存在，请直接写出P点坐标；若不存在，请说明理由．

10、如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB＝OC．

（1）求点B的坐标；

（2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；

（3）在

（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，连接EF．当t为何值时，

＝

？

11、如图，抛物线y＝ax2＋bx＋c与x轴交于点A、B，与y轴交于点C，OC＝4，OA＝2OC，且抛物线的对称轴为直线x＝－3．

（1）求该抛物线的函数表达式；

（2）矩形DEFG的边DE在线段AB上，顶点F、G分别在AC、BC上，设OD＝m，矩形DEFG的面积为S，当S取最大值时，连结DF并延长至点H，使FH＝

DF，求出此时点H的坐标；

（3）若点Q是抛物线上一点，且横坐标为－4，点P是y轴上一点，是否存在这样的点P，使得△BPQ是直角三角形，若存在，求出点P的坐标，若不存在，请说明理由．

12、如图，△ABC是等边三角形，AB＝

，⊙O是△ABC的外接圆，点D在上（与点A、C不重合），连结AD并延长交BC的延长线于E．

（1）设AD＝x，AE＝y，求y关于x的函数关系式，并写出自变量x的取值范围；

（2）若△DBE是以DB、DE为腰的等腰三角形，求AD的长．

13、如图，已知抛物线经过A（－1，0）、B（3，0）、N（2，－3）三点，顶点为D，且与y轴相交于点C．

（1）求抛物线的解析式；

（2）若直线y＝kx＋d经过C、D两点，且与x轴交于点E，试证明四边形AECN是平行四边形；

（3）在抛物线的对称轴上是否存在点P，使得以点P为圆心的圆经过A、B两点，并且与直线CD相切，若存在，求出P点的坐标；若不存在，说明理由．

14、如图，AB是⊙O的直径，点C在⊙O上，OD⊥AB，交AC的延长线于点D，交⊙O于点F，连结OC、BC，BC交OD于点E．

（1）求证：

∠OCE＝∠ODC；

（2）

若⊙O的半径为2，当点C在上运动（与点A、F不重合）时，设OE＝x，△AOD的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围．

15、如图，四边形OABC是一张放在平面直角坐标系的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA＝15，OC＝9，在AB上取一点M，使得△CBM沿CM翻折后，点B落在x轴上，记作N点．

（1）求N点、M点的坐标；

（2）将抛物线y＝x2－36向右平移a（0＜a＜10）个单位后，得到抛物线l，l经过N点，求抛物线l的解析式；

（3）①抛物线l的对称轴上存在点P，使得P点到M、N两点的距离之差最大，求P点的坐标；②若点D是线段OC上的一个动点（不与O、C重合），过点D作DE∥OA交CN于E，设CD的长为m，△PDE的面积为S，求S与m之间的函数关系式，并说明S是否存在最大值．若存在，请求出最大值；若不存在，请说明理由．

16、如图，已知AB是⊙O的直径，弦CD⊥AB交AB于E，F是DC延长线上的一点，FA、FB与⊙O分别交于M、G，GE的延长线交⊙O于N，连结AN．

（1）求证：

AB平分∠MAN；

（2）若N是的中点，求证：

BE＋EF＝

AM；

（3）若⊙O的半径为5，EF＝2CE＝6，求AN的长．

17、如图，二次函数y＝－x2＋ax＋b的图象与x轴交于A（－

，0），B（2，0）两点，且与y轴交于点C．

（1）求该抛物线的解析式，并判断△ABC的形状；

（2）在x轴上方的抛物线上有一点D，且以A、C、D、B四点为顶点的四边形是等腰梯形，请直接写出D点的坐标；

（3）在此抛物线上是否存在点P，使得以A、C、B、P四点为顶点的四边形是直角梯形？

若存在，求出P点的坐标；若不存在，说明理由．

18、如图1，已知矩形ABED，点C是边DE的中点，且AB＝2AD．

（1）判断△ABC的形状，并说明理由；

（2）保持图1中ABC的固定不变，绕点C旋转DE所在的直线MN到图2中的位置（当垂线段AD、BE在直线MN的同侧），试探究线段AD、BE、DE长度之间有什么关系？

并给予证明；

（3）保持图2中△ABC的固定不变，继续绕点C旋转DE所在的直线MN到图3中的位置（当垂线段AD、BE在直线MN的异侧）．试探究线段AD、BE、DE长度之间有什么关系？

并给予证明．