数学建模题目A.doc
《数学建模题目A.doc》由会员分享,可在线阅读,更多相关《数学建模题目A.doc(5页珍藏版)》请在冰豆网上搜索。
矿脉样本点回归模型讨论分析
问题提出:
一矿脉有13个相邻样本点,人为地设定一原点,现测得各样本点对原点的距离x,与该样本点处某种金属含量y的一组数据,为了看出x,y的关系建立合适的回归模型,如二次曲线、双曲线、对数曲线等,并比较它们的优劣。
建立模型:
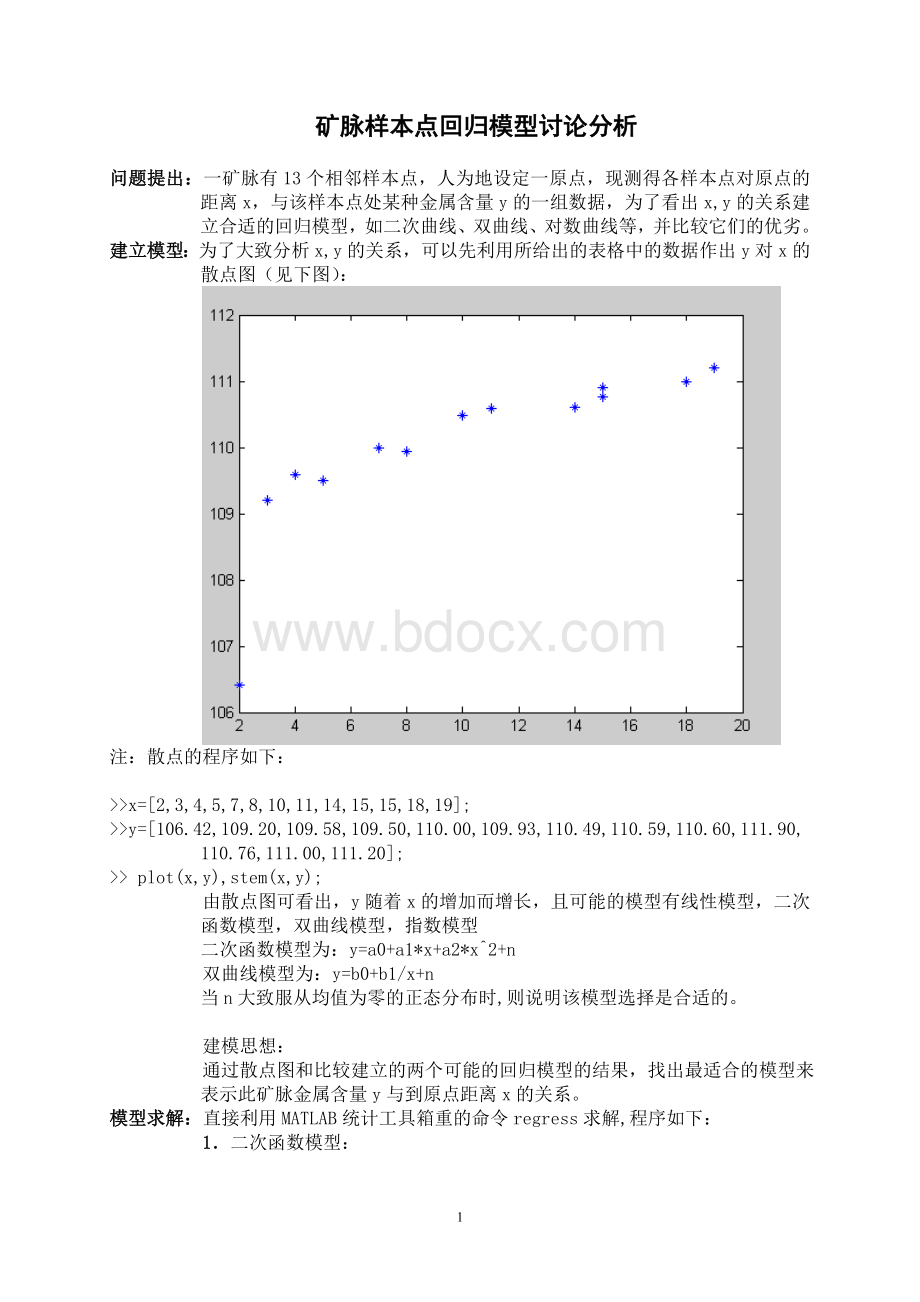
为了大致分析x,y的关系,可以先利用所给出的表格中的数据作出y对x的散点图(见下图):
注:
散点的程序如下:
>>x=[2,3,4,5,7,8,10,11,14,15,15,18,19];
>>y=[106.42,109.20,109.58,109.50,110.00,109.93,110.49,110.59,110.60,111.90,110.76,111.00,111.20];
>>plot(x,y),stem(x,y);
由散点图可看出,y随着x的增加而增长,且可能的模型有线性模型,二次函数模型,双曲线模型,指数模型
二次函数模型为:
y=a0+a1*x+a2*x^2+n
双曲线模型为:
y=b0+b1/x+n
当n大致服从均值为零的正态分布时,则说明该模型选择是合适的。
建模思想:
通过散点图和比较建立的两个可能的回归模型的结果,找出最适合的模型来表示此矿脉金属含量y与到原点距离x的关系。
模型求解:
直接利用MATLAB统计工具箱重的命令regress求解,程序如下:
1.二次函数模型:
y=[106.42;109.20;109.58;109.50;110.00;109.93;110.49;110.59;110.60;110.90;110.76;111.00;111.20];
x=[122^2;133^2;144^2;155^2;177^2;188^2;11010^2;11111^2;11414^2;11515^2;11515^2;11818^2;11919^2];
[b,bint,r,rint,stats]=regress(y,x,0.05)
b=
106.9522
0.5271
-0.0170
bint=
105.4769108.4275
0.18960.8645
-0.0329-0.0011
r=
-1.5182
0.8198
0.7919
0.3380
0.1923
-0.1495
-0.0310
-0.1007
-0.3956
-0.1292
-0.2692
0.0744
0.3769
rint=
-1.7369-1.2995
-0.32631.9660
-0.45032.0341
-1.04631.7223
-1.20361.5881
-1.53311.2341
-1.39681.3348
-1.46451.2631
-1.76210.9709
-1.52761.2693
-1.65661.1183
-1.17131.3200
-0.64961.4035
stats=
0.775917.31120.00060.4182
2.双曲线模型:
y=[106.42;109.20;109.58;109.50;110.00;109.93;110.49;110.59;110.60;110.90;110.76;111.00;111.20];
x=[11/2;11/3;11/4;11/5;11/7;11/8;11/10;11/11;11/14;11/15;11/15;11/18;11/19];
[b,bint,r,rint,stats]=regress(y,x,0.05)
b=
111.4405
-9.0300
bint=
111.1068111.7743
-10.6711-7.3889
r=
-0.5056
0.7695
0.3970
-0.1345
-0.1505
-0.3818
-0.0475
-0.0296
-0.1955
0.0615
-0.0785
0.0611
0.2347
rint=
-0.8402-0.1709
0.31741.2215
-0.29641.0904
-0.88830.6192
-0.90590.6048
-1.09480.3312
-0.80320.7082
-0.78350.7243
-0.93130.5403
-0.68390.8068
-0.82310.6661
-0.68000.8022
-0.48810.9576
stats=
0.9302146.67330.00000.1184
结果分析与检验:
由上述程序运行结果得:
二次函数模型
参数
参数估计值
置信区间
a0
106.9522
[105.4769108.4275]
a1
0.5271
[0.18960.8645]
a2
-0.0170
[-0.0329-0.0011]
R^2=0.7759F=17.3112p=0.0006
双曲线模型
参数
参数估计值
置信区间
b0
111.4405
[111.1068111.7743]
b1
-9.0300
[-10.6711-7.3889]
R^2=0.9302F=146.6733p=0.0000
从以上的这两个表中可以看到:
虽然两个模型的置信区间都不包含零点,即两种模型都不能说明回归变量x不是太显著的,但是双曲线模型中的相关系数R^2比二次函数模型要大,且与1很接近;同时双曲线模型中F的概率值p=0.0000,很小,远远小于0.05.
这就说明双曲线模型更好的符合了实际问题,所以可以得出此矿脉各样本点金属含量与其到原点距离的关系近似符合双曲线关系。
模型评价:
模型各参数达到要求,可用。
参考文献:
刘慧颖.MATLABR2006a基础教程.清华大学出版社.2007.245页.
姜启源谢金星.数学模型(第三版).高等教育出版社.2003.294页
-297页。
5