数字信号处理实验例题.docx
《数字信号处理实验例题.docx》由会员分享,可在线阅读,更多相关《数字信号处理实验例题.docx(25页珍藏版)》请在冰豆网上搜索。
数字信号处理实验例题
实验一离散时间信号与系统
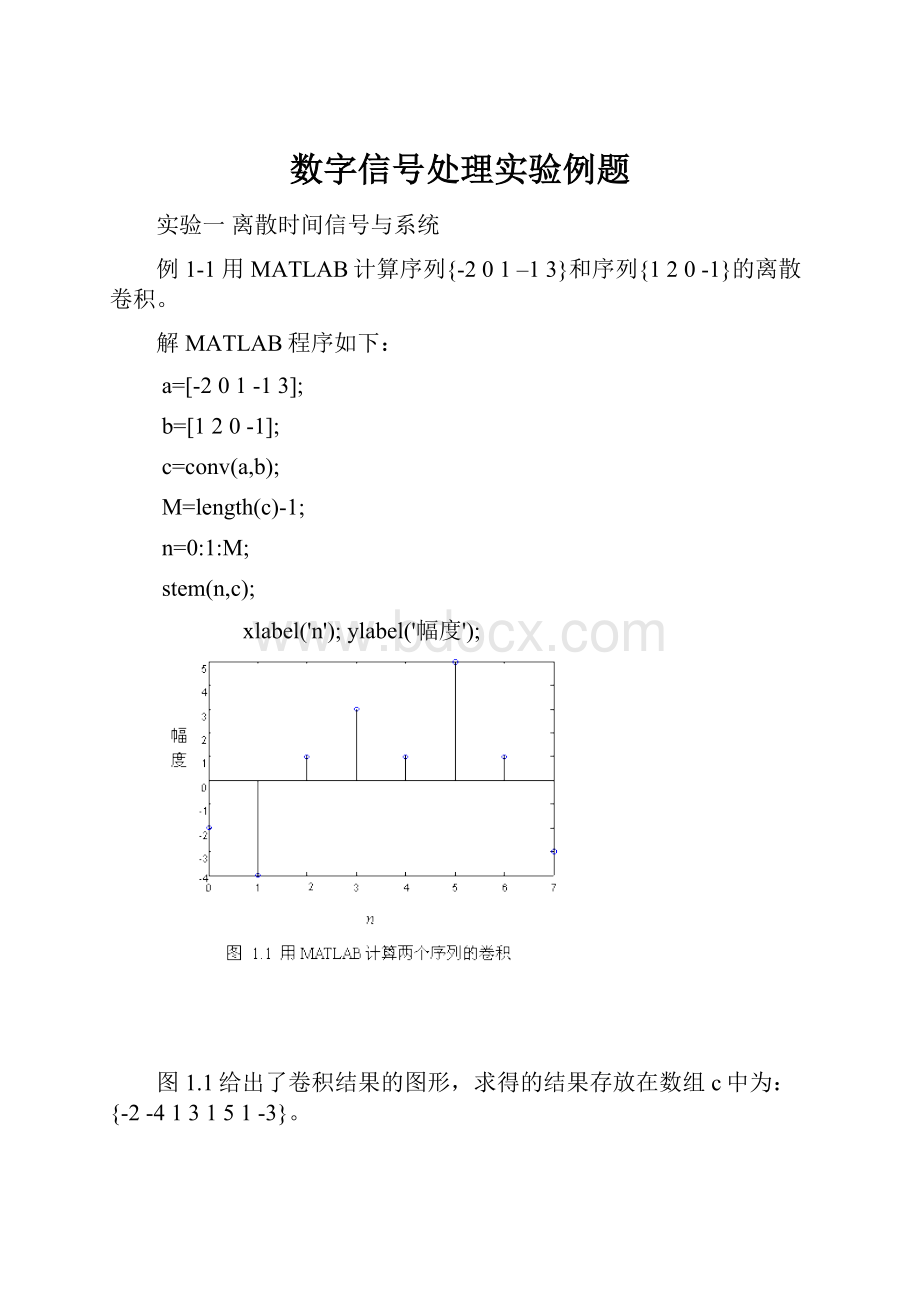
例1-1用MATLAB计算序列{-201–13}和序列{120-1}的离散卷积。
解MATLAB程序如下:
a=[-201-13];
b=[120-1];
c=conv(a,b);
M=length(c)-1;
n=0:
1:
M;
stem(n,c);
xlabel('n');ylabel('幅度');
图1.1给出了卷积结果的图形,求得的结果存放在数组c中为:
{-2-413151-3}。
例1-2用MATLAB计算差分方程
当输入序列为
时的输出结果
。
解MATLAB程序如下:
N=41;
a=[0.8-0.440.360.22];
b=[10.7-0.45-0.6];
x=[1zeros(1,N-1)];
k=0:
1:
N-1;
y=filter(a,b,x);
stem(k,y)
xlabel('n');ylabel('幅度')
图1.2给出了该差分方程的前41个样点的输出,即该系统的单位脉冲响应。
例1-3用MATLAB计算例1-2差分方程
所对应的系统函数的DTFT。
解例1-2差分方程所对应的系统函数为:
其DTFT为
用MATLAB计算的程序如下:
k=256;
num=[0.8-0.440.360.02];
den=[10.7-0.45-0.6];
w=0:
pi/k:
pi;
h=freqz(num,den,w);
subplot(2,2,1);
plot(w/pi,real(h));grid
title('实部')
xlabel('\omega/\pi');ylabel('幅度')
subplot(2,2,2);
plot(w/pi,imag(h));grid
title('虚部')
xlabel('\omega/\pi');ylabel('Amplitude')
subplot(2,2,3);
plot(w/pi,abs(h));grid
title('幅度谱')
xlabel('\omega/\pi');ylabel('幅值')
subplot(2,2,4);
plot(w/pi,angle(h));grid
title('相位谱')
xlabel('\omega/\pi');ylabel('弧度')
实验二离散傅里叶变换及其快速算法
例2-1对连续的单一频率周期信号按采样频率
采样,截取长度N分别选N=20和N=16,观察其DFT结果的幅度谱。
解此时离散序列
,即k=8。
用MATLAB计算并作图,函数fft用于计算离散傅里叶变换DFT,程序如下:
k=8;
n1=[0:
1:
19];
xa1=sin(2*pi*n1/k);
subplot(2,2,1)
plot(n1,xa1)
xlabel('t/T');ylabel('x(n)');
xk1=fft(xa1);xk1=abs(xk1);
subplot(2,2,2)
stem(n1,xk1)
xlabel('k');ylabel('X(k)');
n2=[0:
1:
15];
xa2=sin(2*pi*n2/k);
subplot(2,2,3)
plot(n2,xa2)
xlabel('t/T');ylabel('x(n)');
xk2=fft(xa2);xk2=abs(xk2);
subplot(2,2,4)
stem(n2,xk2)
xlabel('k');ylabel('X(k)');
计算结果示于图2.1,(a)和(b)分别是N=20时的截取信号和DFT结果,由于截取了两个半周期,频谱出现泄漏;(c)和(d)分别是N=16时的截取信号和DFT结果,由于截取了两个整周期,得到单一谱线的频谱。
上述频谱的误差主要是由于时域中对信号的非整周期截断产生的频谱泄漏。
例2-2用FFT计算两个序列
的互相关函数
。
解用MATLAB计算程序如下:
x=[13-112331];
y=[21-1120-13];
k=length(x);
xk=fft(x,2*k);
yk=fft(y,2*k);
rm=real(ifft(conj(xk).*yk));
rm=[rm(k+2:
2*k)rm(1:
k)];
m=(-k+1):
(k-1);
stem(m,rm)
xlabel('m');ylabel('幅度');
其计算结果如图2.2所示。
例2-3计算两个序列的的互相关函数,其中
x(n)={23521–100123530–1–2012}
y(n)=x(n-4)+e(n),e(n)为一随机噪声,在MATLAB中可以用随机函数rand产生
解用MATLAB计算程序如下:
x=[23521-100123530-1-2012];
y=[000023521-100123530-1-2012];
k=length(y);
e=rand(1,k)-0.5;
y=y+e;
xk=fft(x,2*k);
yk=fft(y,2*k);
rm=real(ifft(conj(xk).*yk));
rm=[rm(k+2:
2*k)rm(1:
k)];
m=(-k+1):
(k-1);
stem(m,rm)
xlabel('m');ylabel('幅度');
计算结果如图2.3(a),我们看到最大值出现在m=4处,正好是y(n)对于x(n)的延迟。
2.3(b)是x(n)的自相关函数,他和y(n)的区别除时间位置外,形状也略不同,这是由于y(n)受到噪声的干扰。
实验三无限长单位脉冲响应(IIR)滤波器的设计方法
例3-1设采样周期T=250μs(采样频率fs=4kHz),用脉冲响应不变法和双线性变换法设计一个三阶巴特沃兹滤波器,其3dB边界频率为fc=1kHz。
[B,A]=butter(3,2*pi*1000,'s');
[num1,den1]=impinvar(B,A,4000);
[h1,w]=freqz(num1,den1);
[B,A]=butter(3,2/0.00025,'s');
[num2,den2]=bilinear(B,A,4000);
[h2,w]=freqz(num2,den2);
f=w/pi*2000;
plot(f,abs(h1),'-.',f,abs(h2),'-');
grid;
xlabel('频率/Hz')
ylabel('幅值/dB')
程序中第一个butter的边界频率2π×1000,为脉冲响应不变法原型低通滤波器的边界频率;第二个butter的边界频率2/T=2/0.00025,为双线性变换法原型低通滤波器的边界频率.图3.1给出了这两种设计方法所得到的频响,虚线为脉冲响应不变法的结果;实线为双线性变换法的结果。
脉冲响应不变法由于混叠效应,使得过渡带和阻带的衰减特性变差,并且不存在传输零点。
同时,也看到双线性变换法,在z=-1即ω=π或f=2000Hz处有一个三阶传输零点,这个三阶零点正是模拟滤波器在Ω=∞处的三阶传输零点通过映射形成的。
例3-2设计一数字高通滤波器,它的通带为400~500Hz,通带内容许有0.5dB的波动,阻带内衰减在小于317Hz的频带内至少为19dB,采样频率为1,000Hz。
wc=2*1000*tan(2*pi*400/(2*1000));
wt=2*1000*tan(2*pi*317/(2*1000));
[N,wn]=cheb1ord(wc,wt,0.5,19,'s');
[B,A]=cheby1(N,0.5,wn,'high','s');
[num,den]=bilinear(B,A,1000);
[h,w]=freqz(num,den);
f=w/pi*500;
plot(f,20*log10(abs(h)));
axis([0,500,-80,10]);
grid;
xlabel('')
ylabel('幅度/dB')
图3.2给出了MATLAB计算的结果,可以看到模拟滤波器在Ω=∞处的三阶零点通过高通变换后出现在ω=0(z=1)处,这正是高通滤波器所希望得到的。
例3-3设计一巴特沃兹带通滤波器,其3dB边界频率分别为f2=110kHz和f1=90kHz,在阻带f3=120kHz处的最小衰减大于10dB,采样频率fs=400kHz。
w1=2*400*tan(2*pi*90/(2*400));
w2=2*400*tan(2*pi*110/(2*400));
wr=2*400*tan(2*pi*120/(2*400));
[N,wn]=buttord([w1w2],[0wr],3,10,'s');
[B,A]=butter(N,wn,'s');
[num,den]=bilinear(B,A,400);
[h,w]=freqz(num,den);
f=w/pi*200;
plot(f,20*log10(abs(h)));
axis([40,160,-30,10]);
grid;
xlabel('频率/kHz')
ylabel('幅度/dB')
图3.3给出了MATLAB计算的结果,可以看出数字滤波器将无穷远点的二阶零点映射为z=±1的二阶零点,数字带通滤波器的极点数是模拟低通滤波器的极点数的两倍。
例3-4一数字滤波器采样频率fs=1kHz,要求滤除100Hz的干扰,其3dB的边界频率为95Hz和105Hz,原型归一化低通滤波器为
w1=95/500;
w2=105/500;
[B,A]=butter(1,[w1,w2],'stop');
[h,w]=freqz(B,A);
f=w/pi*500;
plot(f,20*log10(abs(h)));
axis([50,150,-30,10]);
grid;
xlabel('频率/Hz')
ylabel('幅度/dB')
图3.4为MATLAB的计算结果
实验四有限长单位脉冲响应(FIR)滤波器的设计方法
例2用凯塞窗设计一FIR低通滤波器,低通边界频率
,阻带边界频率
,阻带衰减
不小于50dB。
解首先由过渡带宽和阻带衰减
来决定凯塞窗的N和
图4.1给出了以上设计的频率特性,(a)为N=30直接截取的频率特性(b)为凯塞窗设计的频率特性。
凯塞窗设计对应的MATLAB程序为:
wn=kaiser(30,4.55);
nn=[0:
1:
29];
alfa=(30-1)/2;
hd=sin(0.4*pi*(nn-alfa))./(pi*(nn-alfa));
h=hd.*wn';
[h1,w1]=freqz(h,1);
plot(w1/pi,20*log10(abs(h1)));
axis([0,1,-80,10]);
grid;
xlabel('归一化频率/p')
ylabel('幅度/dB')
例4-2利用雷米兹交替算法,设计一个线性相位低通FIR数字滤波器,其指标为:
通带边界频率fc=800Hz,阻带边界fr=1000Hz,通带波动
阻带最小衰减At=40dB,采样频率fs=4000Hz。
解
在MATLAB中可以用remezord和remez两个函数设计,其结果如图4.2,MATLAB程序如下:
fedge=[8001000];
mval=[10];
dev=[0.05590.01];
fs=4000;
[N,fpts,mag,wt]=remezord(fedge,mval,dev,fs);
b=remez(N,fpts,mag,wt);
[h,w]=freqz(b,1,256);
plot(w*2000/pi,20*log10(abs(h)));
grid;
xlabel('频率/Hz')
ylabel('幅度/dB')
函数remezord中的数组fedge为通带和阻带边界频率,数组mval是两个边界处的幅值,而数组dev是通带和阻带的波动,fs是采样频率单位为Hz。
第5章数字信号处理系统的实现
例5-1求下列直接型系统函数的零、极点,并将它转换成二阶节形式
解用MATLAB计算程序如下:
num=[1-0.1-0.3-0.3-0.2];
den=[10.10.20.20.5];
[z,p,k]=tf2zp(num,den);
m=abs(p);
disp('零点');disp(z);
disp('极点');disp(p);
disp('增益系数');disp(k);
sos=zp2sos(z,p,k);
disp('二阶节');disp(real(sos));
zplane(num,den)
输入到“num”和“den”的分别为分子和分母多项式的系数。
计算求得零、极点增益系数和二阶节的系数:
零点
0.9615
-0.5730
-0.1443+0.5850i
-0.1443-0.5850i
极点
0.5276+0.6997i
0.5276-0.6997i
-0.5776+0.5635i
-0.5776-0.5635i
增益系数
1
二阶节
1.0000-0.3885-0.55091.00001.15520.6511
1.00000.28850.36301.0000-1.05520.7679
系统函数的二阶节形式为:
极点图见图5.1。
例5-2分析五阶椭圆低通滤波器的量化效应,其截止频率为0.4
,通带纹波为0.4dB,最小的阻带衰减为50dB。
对滤波器进行截尾处理时,使用函数a2dT.m.。
解用以下MATLAB程序分析量化效应
clf;
[b,a]=ellip(5,0.4,50,0.4);
[h,w]=freqz(b,a,512);
g=20*log10(abs(h));
bq=a2dT(b,5);
aq=a2dT(a,5);
[hq,w]=freqz(bq,aq,512);
gq=20*log10(abs(hq));
plot(w/pi,g,'b',w/pi,gq,'r:
');
grid;
axis([01-805]);
xlabel('\omega/\pi');
ylabel('Gain,dB');
legend('量化前','量化后');
figure
[z1,p1,k1]=tf2zp(b,a);
[z2,p2,k2]=tf2zp(bq,aq);
zplaneplot([z1,z2],[p1,p2],{'o','x','*','+'});
legend('量化前的零点','量化后的零点','量化前的极点','量化后的极点');
图5.1(a)表示系数是无限精度的理想滤波器的频率响应(以实线表示)以及当滤波器系数截尾到5位时的频率响应(以短线表示)。
由图可知,系数量化对频带的边缘影响较大,经系数量化后,增加了通带的波纹幅度,减小了过渡带宽,并且减小了最小的阻带衰减。
图5.1(b)给出了系数量化以前和系数量化以后的椭圆低通滤波器的零极点位置。
由图可知,系数的量化会使零极点的位置与它们的理想的标称位置相比发生显著的改变。
在这个例子中,靠近虚轴的零点的位置变动最大,并且移向靠它最近的极点的位置。
只要对程序稍作改变就可以分析舍入量化的影响。
为了研究二进制数量化效应对数字滤波器的影响,首先需要将十进制表示的滤波器系数转换成二进制数并进行量化,二进制数的量化既可以通过截尾法也可以通过舍入法实现。
我们提供了如下的两个MATLAB程序:
a2dT.m和a2dR.m,这两段程序分别将向量d中的每一个数按二进制数进行截尾或舍入量化,量化的精度是小数点以后保留b位,量化后返回的向量为beq。
functionbeq=a2dT(d,b)
%beq=a2dT(d,b)将十进制数利用截尾法得到b位的二进制数,
%然后将该二进制数再转换为十进制数
m=1;d1=abs(d);
whilefix(d1)>0
d1=abs(d)/(2^m);
m=m+1;
end
beq=fix(d1*2^b);
beq=sign(d).*beq.*2^(m-b-1);
functionbeq=a2dR(d,b)
%beq=a2dR(d,b)将十进制数利用舍入法得到b位的二进制数
%然后将该二进制数再转换为十进制数
m=1;d1=abs(d);
whilefix(d1)>0
d1=abs(d)/(2^m);
m=m+1;
end
beq=fix(d1*2^b+.5);
beq=sign(d).*beq.*2^(m-b-1);
第7章多采样率信号处理
例7-1在时域上显示一个
信号频率为0.042
的正弦信号,然后以抽取因子3降采样率,并在时域上显示相应的结果,比较两者在时域上的特点。
解用MATLAB计算程序如下:
M=3;%down-samplingfactor=3;
fo=0.042;%signalfrequency=0.042;
%generatetheinputsinusoidalsequence
n=0:
N-1;
m=0:
N*M-1;
x=sin(2*pi*fo*m);
%generatethedown-samplingsquence
y=x([1:
M:
length(x)]);
subplot(2,1,1)
stem(n,x(1:
N));
title('输入序列');
xlabel('时间/n');
ylabel('幅度');
subplot(2,1,2)
stem(n,y);
title(['输出序列,抽取因子为',num2str(M)]);
xlabel('时间/n');ylabel('幅度');
图7.1
信号频率为0.042
的正弦信号和降采样率后的情况
例7-2用汉明窗设计一长度为32的线性相位QMF滤波器组。
解采用MATLAB设计,调用fir2函数设计公共低通滤波器,参数缺省即为汉明窗,程序如下:
b1=fir2(31,[0,0.4,0.5,0.55,0.6,1],[1,1,1,0.06,0,0]);
fork=1:
32b2(k)=((-1)^(k-1))*b1(k);
end
[H1z,w]=freqz(b1,1,256);
h1=abs(H1z);g1=20*log10(h1);
[H2z,w]=freqz(b2,1,256);
h2=abs(H2z);g2=20*log10(h2);
figure
(1);
plot(w/pi,g1,'-',w/pi,g2,'--');
axis([0,1,-100,10]);
grid
xlabel('\omega/\pi');ylabel('幅度,dB');
sum=h1.*h1+h2.*h2;
d=10*log10(sum);
figure
(2)
plot(w/pi,d);grid;
xlabel('\omega/\pi');ylabel('误差,dB');
axis([0,1,-0.3,0.3]);
图7.2(a)是一个N=32的汉明窗设计结果,图中实线表示
=
的低通频响,虚线表示它的镜像
=
。
图7.2(b)是基于这种设计方法的分析/综合滤波器组的整个频响
+
。
从这个图可见,重建误差小于±0.05dB。
由于汉明窗设计的频
率响应在通带中近乎是平坦的,因此最大重建误差发生在这个滤波器的通带边界和过渡带内。
.