计量经济学庞浩习题.docx

计量经济学庞浩习题.docx

《计量经济学庞浩习题.docx》由会员分享，可在线阅读，更多相关《计量经济学庞浩习题.docx（17页珍藏版）》请在冰豆网上搜索。

计量经济学庞浩习题

6.1

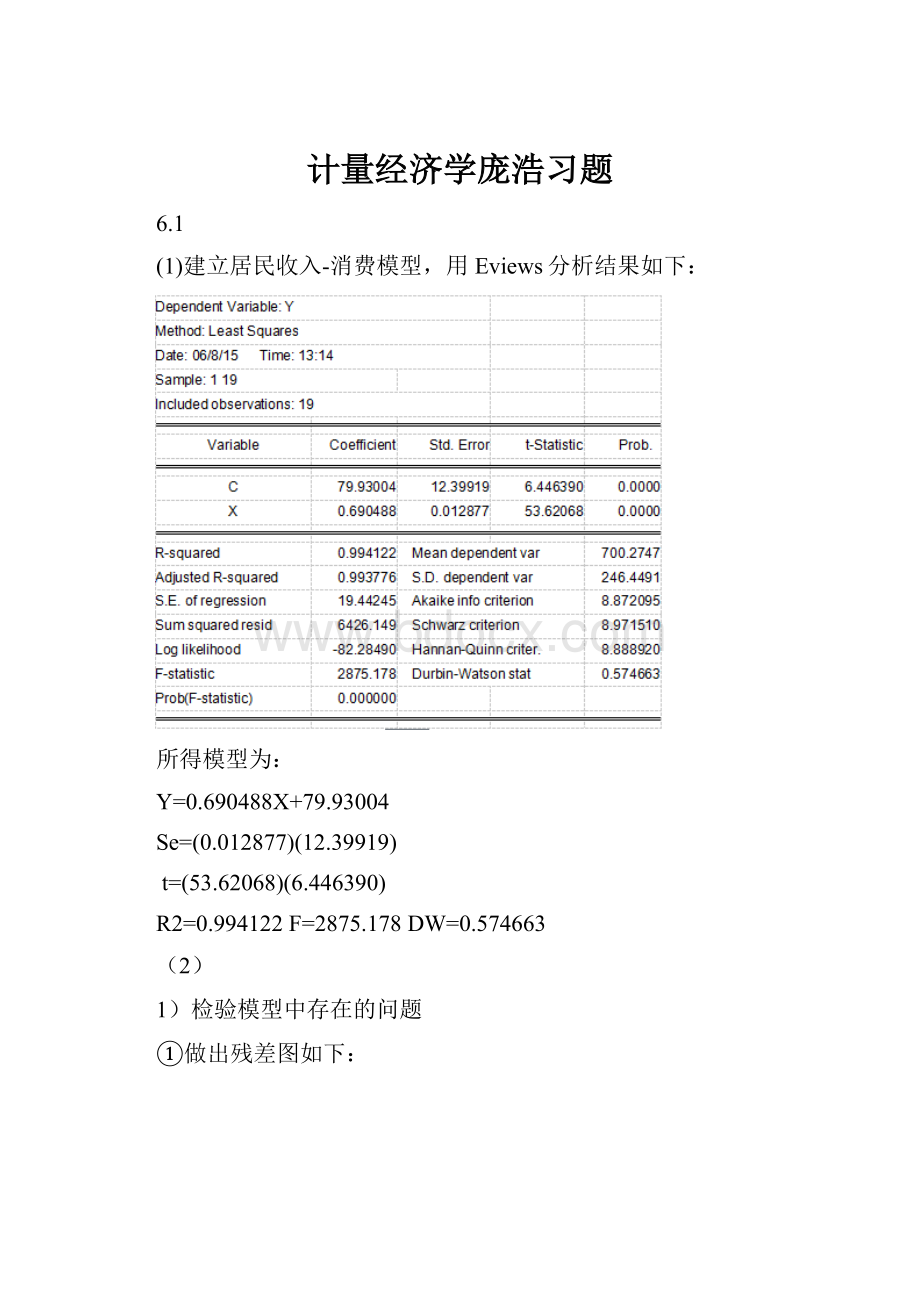
（1）建立居民收入-消费模型，用Eviews分析结果如下：

所得模型为：

Y=0.690488X+79.93004

Se=（0.012877）（12.39919）

t=（53.62068）（6.446390）

R2=0.994122F=2875.178DW=0.574663

（2）

1）检验模型中存在的问题

①做出残差图如下：

残差连续为正和连续为负，表明残差项存在一阶自相关。

②该回归方程可决系数较高，回归系数均显著。

对样本量为19，一个解释变量的模型，5%的显著水平，查DW统计表可知，dL=1.180，dU=1.401，模型中DW=0.574663,

③对模型进行BG检验，用Eviews分析结果如下：

如上表显示，LM=TR2=7.425086，其p值为0.0244，表明存在自相关。

2）对模型进行处理：

采取广义差分法

a）为估计自相关系数ρ。

对et进行滞后一期的自回归，用EViews分析结果如下：

由上可知，ρ=0.657352

b）对原模型进行广义差分回归

由上图可知回归方程为：

Yt*=35.97761+0.668695Xt*

Se=（8.103546）（0.020642）

t=（4.439737）（32.39512）

R2=0.984983F=1049.444DW=1.830746

式中，Yt*=Yt-0.657352Yt-1,Xt*=Xt-0.657352Xt-1

由于使用了广义差分数据，样本容量减少了1个，为18个。

查5%显著水平的DW统计表可知，dL=1.158,dU=1.391模型中DW=1,830746，du

可决系数R2，t，F统计量也均达到理想水平。

由差分方程，β1=35.97761/（1-0.657352）=104.9987

由此最终的消费模型为：

Yt=104.9987+0.668695Xt

（3）经济意义：

人均实际收入每增加1元，平均说来人均时间消费支出将增加0.669262元。

6.2

（1）

用Eviews分析结果如下：

所得模型为：

Y=0.265056X-1668.731

Se=（0.011719）（555.7701）

t=（22.61745）（-3.002555）

R2=0.953406F=511.5491DW=0.601376

DW=0.601376,查表可知DW，0≤DW≤dL误差项存在着自相关.

做出残差图如下：

残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶自相关。

（2）对模型进行处理：

1采取广义差分法

为估计自相关系数ρ。

对et进行滞后一期的自回归，用EViews分析结果如下：

由上可知，ρ=0.700133

对原模型进行广义差分回归，用Eviews进行分析所得结果如下：

由上图可知回归方程为：

Yt*=-490.4053+0.260988Xt*

Se=（419.9286）（0.023761）

t=（-1.167831）（10.8404）

R2=0.834081F=120.6492DW=1.652168

式中，Yt*=Yt-0.700133Yt-1,Xt*=Xt-0.700133Xt-1

由于使用了广义差分数据，样本容量减少了1个，为26个。

查5%显著水平的DW统计表可知，dL=1.302,dU=1.1.461模型中DW=1,652168，du

可决系数R2，t，F统计量也均达到理想水平。

由差分方程，β1=-490.4053/（1-0.700133）=-1635.4093

最终的模型为:

Y=-1635.4093+0.260988X

6.3

（1）

用Eviews分析结果如下：

所得模型为：

Y=0.784106X-2123.864

Se=（0.041276）（324.8012）

t=（18.99680）（-6.538966）

R2=0.937643F=360.8784DW=0.440822

经济意义：

国内生产总值每增加10亿元，平均说来股票价值指数将增加0.784106。

（2）

DW=0.440822,查表可知DW的上下界，0≤DW≤dL误差项存在着自相关。

做出残差图如下：

残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶自相关。

对模型进行处理：

采取广义差分法

为估计自相关系数ρ。

对et进行滞后一期的自回归，用EViews分析结果如下：

ρ=0.768816

对原模型进行广义差分回归，用Eviews进行分析所得结果如下：

由上图可知回归方程为：

Yt*=-653.9415+0.857233Xt*

Se=（220.3093）（0.101264）

t=（-2.968289）（8.465330）

R2=0757030F=71.66181DW=0.902421

式中，Yt*=Yt-0.768816Yt-1,Xt*=Xt-0,768816Xt-1

由差分方程，β1=-653.9415/（1-0.768816）=--2828.662

最终的模型为:

Y=-2828.662+0.8572233X

样本容量25个，在5%显著水平下DW上下界，dL=1.288,dU=1.454.模型中DW=0.902421，依然存在自相关性。

6.4

（1）

1）针对对数模型，用Eviews分析结果如下：

所得模型为：

lnY=0,951090lnX+2.171041

se=（0.038897）（0.241025）

t=（24.45123）（9.007529）

R2=0.969199F=597.8626DW=1.159788

2）检验模型的自相关性

该回归方程可决系数较高，回归系数均显著。

对样本量为21，一个解释变量的模型，5%的显著水平，查DW统计表可知，dL=1.221，dU=1.420，模型中DW=1.159788

做出残差图如下：

残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶自相关。

（2）用广义差分法处理模型：

1）为估计自相关系数ρ。

对et进行滞后一期的自回归，用EViews分析结果如下：

由上可知，ρ=0.400234

2）对原模型进行广义差分回归，用Eviews进行分析所得结果如下：

由上图可知回归方程为：

Yt*=-13.03313+6.571250Xt*

Se=（208.6891）（0.508933）

t=（-0.062452）（12.91183）

R2=0.902533F=166.7154DW=1.966598

式中，Yt*=Yt-0.400234Yt-1,Xt*=Xt-0,400234Xt-1

4）由差分方程:

β1=-13.03313/（1-0.400234）=-21.730358

最终的模型为:

Y=-21.730358+6.57125X

样本容量20个，在5%显著水平下DW上下界，dL=1.201,dU=1.411,模型中DW=1.966598，dU

（3）对于此模型，用Eviews分析结果如下：

模型样本容量为20，dL=1.201,dU=1.411模型中DW=1.590363，dU

6.5

（1）

1）针对对数模型，用Eviews分析结果如下：

LOGPRICE=-8.00223-0.004297HRAIN+0.000264WRAIN+0.394039DEGREE+0.035379TINE

结果意义：

在其他变量不变的情况下，收获季节的降雨量每增加1，波尔多葡萄酒的价格平均减少0.004297.收获前一年冬季的降雨量每增加1，波尔多葡萄酒的价格平均增加0.000264,种植季节的平均温度每增加1，波尔多葡萄酒的价格平均增加0.394039。

酿制年份到1989年的年数每增加1，波尔多葡萄酒的价格平均增加0.035379。

（2）在5%显著水平下DW上下界，dL=1.104,dU=1.747，模型中DW=2.262869，4-dU

（3）若剔除HRAIN后，用Eviews分析结果如下：

LOGPRICE=-9.936478+0.44671DEGREE+0.000955WRAIN+0.036455SER05

（4）后者更好。

因为在5%显著水平下DW上下界，dL=1.181,dU=1.65

模型中DW=2.229941，dU

可决系数R2，t，F统计量也均达到理想水平。