一次函数图像与行程问题练习题.docx

一次函数图像与行程问题练习题.docx

《一次函数图像与行程问题练习题.docx》由会员分享，可在线阅读，更多相关《一次函数图像与行程问题练习题.docx（10页珍藏版）》请在冰豆网上搜索。

一次函数图像与行程问题练习题

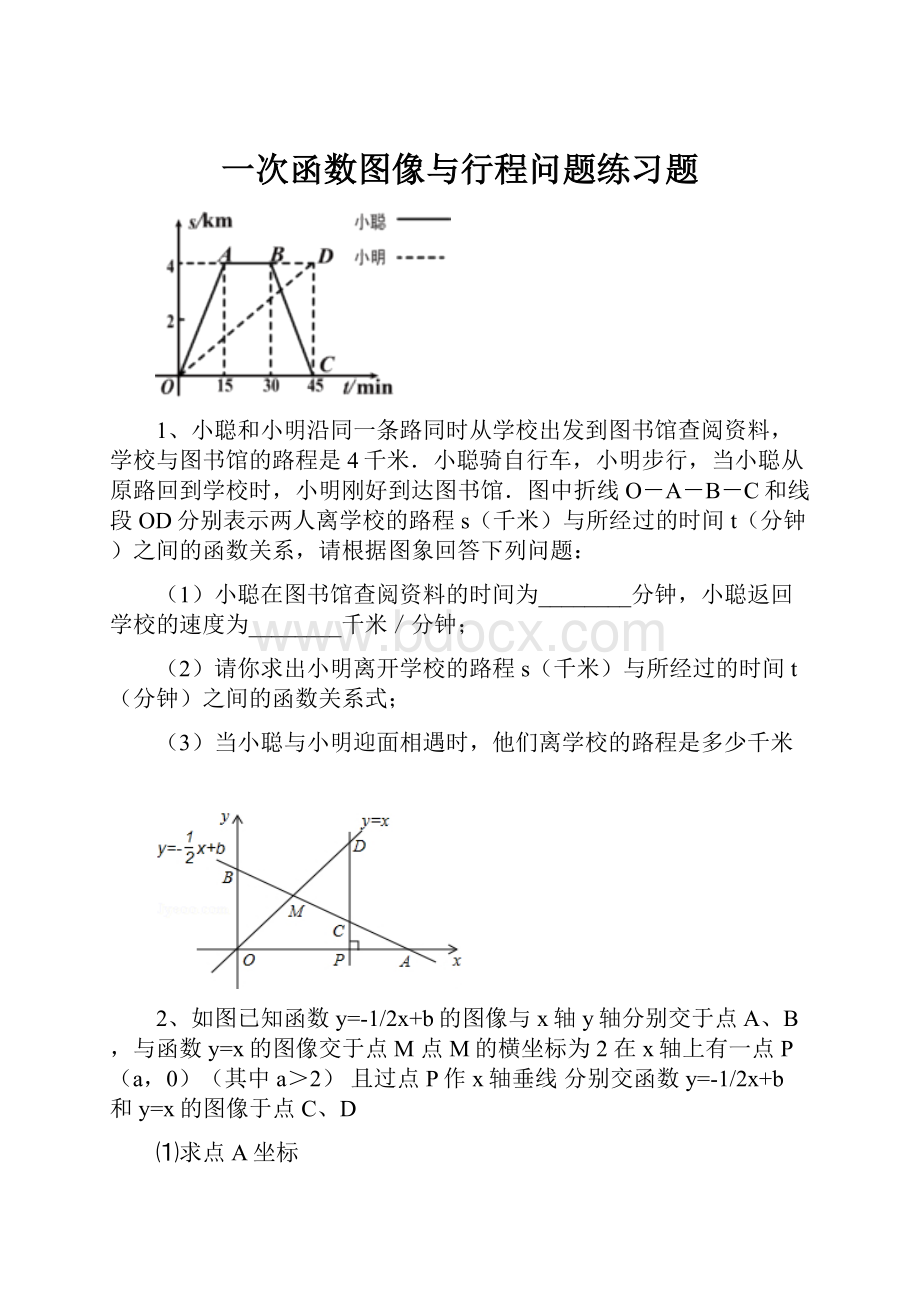
1、小聪和小明沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米．小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆．图中折线O－A－B－C和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：

（1）小聪在图书馆查阅资料的时间为________分钟，小聪返回学校的速度为________千米／分钟；

（2）请你求出小明离开学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系式；

（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米

2、如图已知函数y=-1/2x+b的图像与x轴y轴分别交于点A、B，与函数y=x的图像交于点M点M的横坐标为2在x轴上有一点P（a，0）（其中a＞2）且过点P作x轴垂线分别交函数y=-1/2x+b和y=x的图像于点C、D

⑴求点A坐标

⑵若OB=CD，求a的值

3、如图，一次函数y=-3/4x+3的图象与x轴和y轴分别交于点A和B，再将△AOB沿直线CD对折，使点A与点B重合、直线CD与x轴交于点C，与AB交于点D．

（1）点A的坐标为（4，0），点B的坐标为（0，3）；

（2）求OC的长度；

（3）在x轴上有一点P，且△PAB是等腰三角形，不需计算过程，直接写出点P的坐标．

4、甲、乙两城市之间开通了动车组高速列车．已知每隔1h有一列速度相同的动车组列车从甲城开往乙城．如图所示，OA是第一列动车组列车离开甲城的距离s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：

（1）点B的横坐标的意义是普通快车发车时间比第一列动车组列车发车时间_____1h（填”早”或”晚”），点B的纵坐标300的意义是_______；

（2）请你在图中直接画出第二列动车组列车离开甲城的路程s（km）与时间t（h）的函数图象；

（3）若普通快车的速度为100km/h，

①求BC的解析式，并写出自变量t的取值范围；

②第二列动车组列车出发多长时间后与普通快车相遇

③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔时间。

5、甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）。

图6中折线OABC、线段DE分别表示甲、乙两车所行路程y（千米）与时间x（小时）之间的函数关系对应的图像（线段AB表示甲出发不足2小时因故停车检修）。

根据图像回答

（1）求乙车所行路程y与时间啊x的函数解析式。

（2）求两车在途中第二次相遇时，它们距出发地的路程。

（3）乙车出发多长时间，两车在途中第一次相遇

6、下图表示甲、乙两名选手在一次自行车越野赛中路程y（km）随时间x（min）变化的图象（全程）。

根据图象回答下列问题：

（1）比赛开始多少分钟时，两人第一次相遇

（2）这次比赛全程是多少千米

（3）比赛开始多少分钟时，两人第二次相遇

7、设甲,乙两车在同一直线公路上匀速行驶,开始时甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度是_________米秒.

8、如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站飞路

程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．

（1）填空：

A，B两地相距　420　千米；

（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；

（3）客、货两车何时相遇

9、从甲地到乙地，先是一段平路，然后是一段上坡路。

小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间。

假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km。

设小明出发xh后，到达离甲地ykm的地方，图中的折线OABCDE表示y与x之间的函数关系.

（1）小明骑车在平路上的速度为km/h；他途中休息了h；

（2）求线段AB，BC所表示的y与

之间的函数关系式；

（3）如果小明两次经过途中某一地点的时间间隔为，那么该地点离甲地多远

10、A，B两地相距1100米，甲从A地出发，乙从B地出发，相向而行，甲比乙先出发2分钟，乙出发7分钟后与甲相遇．设甲、乙两人相距y米，甲行进的时间为t分钟，y与t之间的函数关系如图所示．请你结合图象探究：

（1）甲的行进速度为每分钟60米，m=9分钟；

（2）求直线PQ对应的函数表达式；

（3）求乙的行进速度．

11、如图,在直线Y=-4/3x＋8与x轴,y轴分别交于点A和点B,M是

OB上的一点,若三角形ABM沿AM折叠,点B恰好落在x轴上的点B’处,求：

（1）点A的坐标为，

点B的坐标为。

（2）求点M的坐标

（3）求直线AM的解析式.

12、如图，在平面直角坐标系xOy中，直线y=-4/3x+8与x轴,y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．

（1）求A点的坐标是，B点的坐标是；

（2）AB的长和点C的坐标；

（3）求直线CD的解析式．

13、已知甲.乙两车分别从相距300km的A.B两地同时出发，相向而行，其中甲到B地后立即返回，下图是它们离各自出发地的距离y（km）与行驶时间x（h）之间的函数图象。

（1）求甲车离出发地的距离y与行驶时间x之间的函数关系式，并写出自变量的取值范围；

（2）当它们行驶到与各自出发地的距离相等时用了小时，求乙车离出发地的距离y与行驶时间x之间的函数关系式，并写出x的范围；

（3）在

（2）的条件下，求它们的行驶过程中相遇的时间。

14、在平面直角坐标系中，直线AB：

y=kx+1，交y轴于点A，交x轴于点B（3,0），平行于y轴的直线x=1，交AB于点D，交x轴于点E，点P是直线x=1上一动点，且在点D的上方，设P（1，a）

（1）求直线AB的解析式和点A的坐标

（2）求三角形ABP的面积（用含a的代数式表示）

（3）当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，直接写出点C的坐标

１５、李明乘车从永康到某景区旅游，同时王红从该景区返回永康。

如图，线段ＯＢ表示李明离永康的路程Ｓ1（ｋｍ）与时间ｔ（ｈ）的函数关系；线段ＡＣ表示王红离永康的路程Ｓ2（ｋｍ）与时间（ｈ）的函数关系。

行驶１小时，李明、王红离永康的路程分别为１００ｋｍ、２８０ｋｍ，王红从景区返回永康用了４.５小时，（假设两人所乘的车在同一线路上行驶）

（1）分别求Ｓ1，Ｓ2关于ｔ的函数表达式；

（2）当ｔ为何值时，他们乘坐的两车相遇；

（3）

当李明到达景区时，王红离永康还有多少千米

16、如图，矩形ABCD中，AB=4cm，BC=3cm，有一动点P从B点沿BC,CD，DA以每分钟1cm的速度移动，移动至A点后停止

（1）求三角形ABP的面积S（cm2）与时间t（分钟）之间的函数关系式；

（2）在直角坐标系中画出函数的图像。

17、在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题：

（1）A、C两村间的距离为　　km，a=　　；

（2）求出图中点P的坐标，并解释该点坐标所表示的实际意义；

（3）乙在行驶过程中，何时距甲10km