九年级二次函数压轴题专题训练含答案和方法指导精品文档.docx

九年级二次函数压轴题专题训练含答案和方法指导精品文档.docx

《九年级二次函数压轴题专题训练含答案和方法指导精品文档.docx》由会员分享，可在线阅读，更多相关《九年级二次函数压轴题专题训练含答案和方法指导精品文档.docx（3页珍藏版）》请在冰豆网上搜索。

九年级二次函数压轴题专题训练含答案和方法指导精品文档

九年级二次函数压轴题专题训练（含答案）

方法:

面积法,化斜为直,韦达定理,几何变换等.

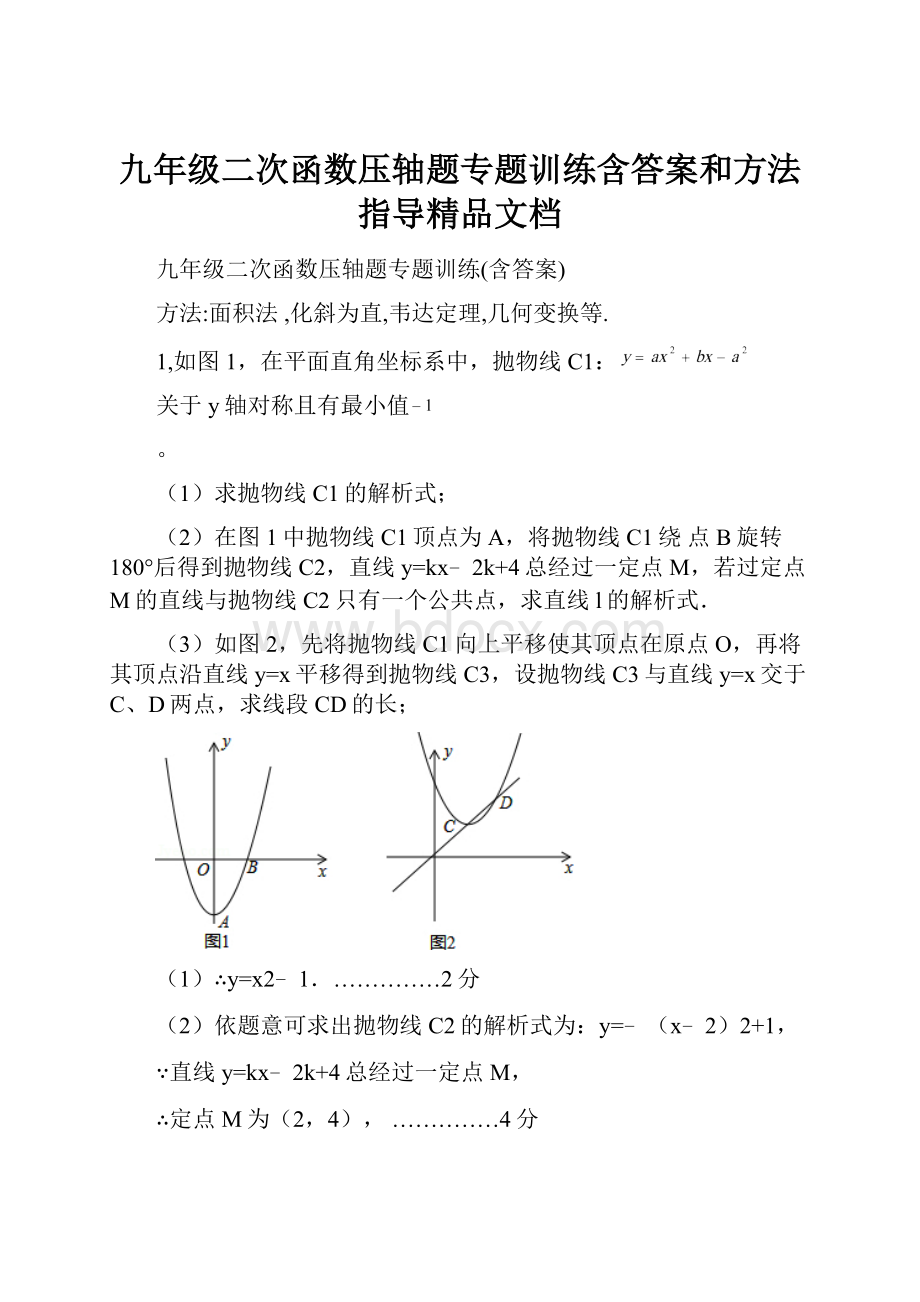
1,如图1，在平面直角坐标系中，抛物线C1：

关于y轴对称且有最小值

。

（1）求抛物线C1的解析式；

（2）在图1中抛物线C1顶点为A，将抛物线C1绕点B旋转180°后得到抛物线C2，直线y=kx﹣2k+4总经过一定点M，若过定点M的直线与抛物线C2只有一个公共点，求直线l的解析式．

（3）如图2，先将抛物线C1向上平移使其顶点在原点O，再将其顶点沿直线y=x平移得到抛物线C3，设抛物线C3与直线y=x交于C、D两点，求线段CD的长；

（1）∴y=x2﹣1．‥‥‥‥‥‥‥2分

（2）依题意可求出抛物线C2的解析式为：

y=﹣（x﹣2）2+1，

∵直线y=kx﹣2k+4总经过一定点M，

∴定点M为（2，4），‥‥‥‥‥‥‥4分

①经过定点M（2，4），与y轴平行的直线l：

x=2与抛物线C3总有一个公共点（2，1）．

②经过定点M（2，4）的直线l为一次函数y=kx﹣2k+4时，与y=﹣（x﹣2）2+1联立方程组，消去y得x2﹣4x+3+kx﹣2k+4=0，

即x2﹣（4﹣k）x+7﹣2k=0，△=k2﹣12=0，得k1=2

，k2=﹣2

，

∴y=2

x+4﹣4

或y=﹣2

x+4+4

，

综上所述，过定点M，共有三条直线l：

x=2或y=2

x+4﹣4

或y=﹣2

x+4+4

，它们分别与抛物线C2只有一个公共点．

（3）设抛物线C3的顶点为（m，m），依题意抛物线C3的解析式为：

y=（x﹣m）2+m，

与直线y=x联立

，

解方程组得：

，

，

∴C（m，m），D（m+1，m+1）

过点C作CM∥x轴，过点D作DM∥y轴，

∴CM=1，DM=1，

∴CD=

．

2,如图，抛物线y＝ax2－4ax＋b交x轴正半轴于A、B两点，交y轴正半轴于C，且OB＝OC＝3

（1）求抛物线的解析式