整理年上海大学插班生招生计划及学校加试科目.docx
《整理年上海大学插班生招生计划及学校加试科目.docx》由会员分享,可在线阅读,更多相关《整理年上海大学插班生招生计划及学校加试科目.docx(23页珍藏版)》请在冰豆网上搜索。
整理年上海大学插班生招生计划及学校加试科目
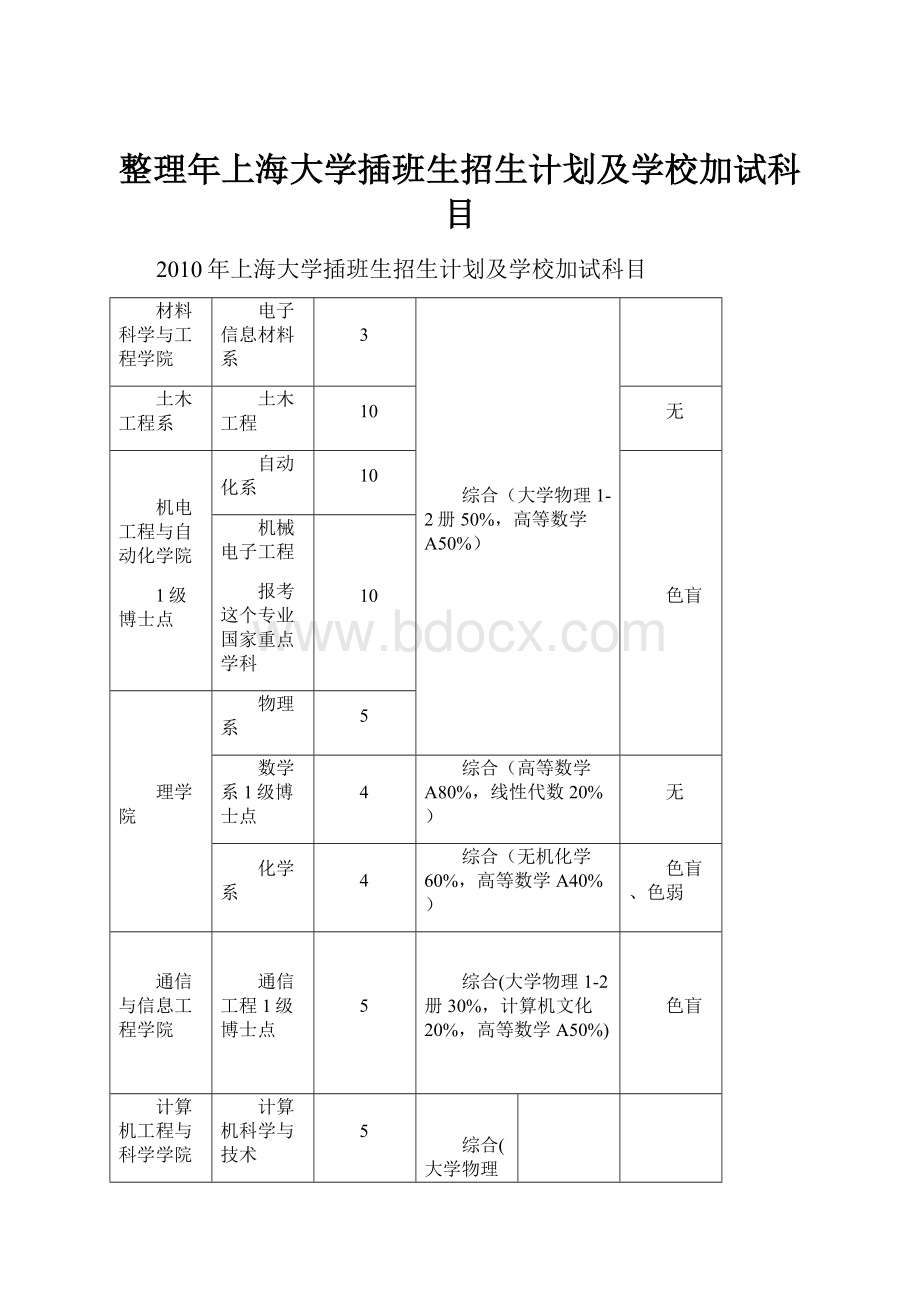
2010年上海大学插班生招生计划及学校加试科目
材料科学与工程学院
电子信息材料系
3
综合(大学物理1-2册50%,高等数学A50%)
土木工程系
土木工程
10
无
机电工程与自动化学院
1级博士点
自动化系
10
色盲
机械电子工程
报考这个专业国家重点学科
10
理学院
物理系
5
数学系1级博士点
4
综合(高等数学A80%,线性代数20%)
无
化学系
4
综合(无机化学60%,高等数学A40%)
色盲、色弱
通信与信息工程学院
通信工程1级博士点
5
综合(大学物理1-2册30%,计算机文化20%,高等数学A50%)
色盲
计算机工程与科学学院
计算机科学与技术
5
综合(大学物理1-2册30%,计算机文化20%,高等数学A50%)
上海大学插班生高数B与A的区别
作者:
招考无忧 发布时间:
2008-07-2521:
28:
58 来源:
招考无忧
总体上说A与B的差别就是:
1、A的难度和知识的广度要高于B
2、A主要偏向于理工科的知识结构范围,B偏向于经济类的计算
具体细节如下:
A要求但B不要求
(1)掌握基本初等函数的性质和图形
(2)掌握极限存在的二个准则,并会利用它们求极限
(3)会用导数描述一些简单的物理量
(4)了解曲率,曲率半径的概念,并会计算
(5)了解求方程近似解的二分法和切线法
(6)了解曲线的切线和法平面及曲面的切平面和法线的的概念,会求它们的方程
(7)三重积分
(8)曲线曲面积分
(9)向量代数与空间解析几何
B要求积分与微分涉及到经济类的应用题和差分方程。
总结:
一般来说把A都搞得很好了,考B一般也会很好。
如还有疑问可自行比对A,B的教学基本要求。
一般考经济类的也有理科生,所以建议学文科和经济类的学生以A的难度为标准复习迎考。
上海大学插班生高等数学A基本要求
作者:
招考无忧 发布时间:
2008-07-2521:
25:
36 来源:
招考无忧
1、函数、极限、连续
(1)、理解函数的概念,掌握函数的表示方法
(2)了解函数的奇偶性、单调性、周期性和有界性
(3)理解复合函数的概念,了解反函数及隐函数的概念。
会建立简单函数关系式
(4)掌握基本初等函数的性质和图形
(5)理解极限的概念,了解分段函数的极限
(6)掌握极限四则运算法则,掌握利用两个重要极限求极限的方法。
(7)掌握极限存在的二个准则,并会利用它们求极限
(8)理解无穷小、无穷大以及无穷小的阶的概念,会利用等价无穷小求极限1
(9)理解函数连续性的概念,会判断函数间断点的类型
(10)了解初等函数的连续性和闭区间上的连续函数的性质,并会应用这些性质
2、导数与微分
(1)理解导数的概念导数的几何意义和物理意义,函数的可导性与连续性之间的关系
(2)掌握导数的四则元算法则和复合函数的求导法,掌握基本初等函数的导数公式。
会求分段函数的一阶二阶导数
(3)了解高阶函数的概念,会求简单的函数的n阶导数,掌握初等函数的二阶导数的求法
(4)会求隐函数和参数方程所确定的函数的一、二阶导数。
(5)了解微分的概念和四则运算
(6)会用导数描述一些简单的物理量
3、中值定理与导数的应用
(1)理解并会应用罗尔定理、拉格朗日定理,利用定理能求方程的根、证明不等式。
了解柯西定理
(2)理解函数的极值概念,掌握用导数判别函数的单调性和求函数极值的方法(3)会用导数描绘图形
(4)会求MAX、MIN的应用问题
(5)掌握洛必达法则求未定式极限的方法
(6)了解曲率,曲率半径的概念,并会计算
(7)了解求方程近似解的二分法和切线法
4、不定积分
(1)理解原函数的概念,理解不定积分的概念及性质
(2)掌握不定积分的基本公式、换元法、分部积分法
5、定积分及其应用
(1)理解定积分的基本概念,定积分的中值定理
(2)理解变限函数及其求导定理,掌握牛顿—莱布尼兹公式
(3)掌握定积分的性质及换元积分法和分部积分法
(4)了解定积分的近似计算方法
(5)掌握定积分在几何上的应用,和物理上的应用
(6)了解广义积分的概念,会计算广义积分
6、级数
(1)理解常数项级数收敛与发散的概念、收敛级数和的概念,掌握级数的基本性质及收敛的必要条件
(2)掌握几何级数、P—级数的收敛性
(3)掌握正向级数的判别法
(4)会用交错级数的莱布尼兹判别法
(5)了解无穷级数绝对收敛与条件收敛的概念,及两者之间的关系
(6)了解函数项级数的收敛域和函数的概念
(7)掌握幂级数的收敛半径,收敛区间及收敛域的求法
(8)了解幂级数在收敛区间内的一些基本性质,会求一些幂级数在收敛区间内的和函数,并会由此求出某些数的项级数的和
(9)了解泰勒公式、泰勒级数,掌握的麦克劳林展开式,会用它们将一些简单函数展开幂级数
(10)了解幂级数在近似计算中得到简单应用
(11)了解傅立叶级数的概念及函数展开成傅立叶级数的狄利克莱定理
(12)会将定义在上函数展开为傅立叶级数,会将定义在上的函数展开为正弦与余弦级数、会些出傅立叶级数的和表达式
7、向量代数与空间解析几何
(1)理解向量的概念及其表示
(2)掌握向量的运算,了解两向量垂直、平行的条件。
了解向量的混合积
(3)掌握单位向量、方向数、方向余弦、向量的坐标表达式以及用坐标表达式进行向量运算的方法
(4)掌握平面方程、直线方程,会用平面直线的相互关系解决有关问题
(5)理解曲面方程的概念,了解常用二次曲面的方程及其图形,会求一坐标轴为旋转曲面及母线平行于坐标轴的柱面方程
(6)了解空间曲线的参数方程和一般方程;了解它在坐标平面上的投影,并会求其方程
8、多元函数微分学
(1)理解多元函数的微分学
(2)理解二元函数的极限与连续的概念以及有界区域上连续函数的性质
(3)理解偏导数于全微分的概念,理解去微分存在的必要条件和充分条件,了解去微分在近似计算中的应用
(4)理解方向导数于梯度的概念并掌握其计算方法
(5)掌握复合函数一阶二阶偏导数的求法
(6)会求隐函数的偏导数
(7)了解曲线的切线和法平面及曲面的切平面和法线的的概念,会求它们的方程
(8)理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘法求条件极值,会求简单多元含函数的最大值与最小值并会解决一些简单的应用问题
9、重积分
(1)理解二重、三重积分的概念,了解重积分的性质
(2)掌握二重积分的计算方法,会计算三重积分
(3)会用重积分求一些几何量与物理量
10、曲线积分与曲面积分
(1)理解两类曲线积分的概念,了解两类曲线积分的性质、了解两类曲线积分的关系
(2)掌握计算两类曲线积分的方法
(3)掌握格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数
(4)了解两类曲面积分的概念、性质及两类曲面积分的关系
(5)掌握计算两类曲面积分的方法
(6)了解高斯公式,会用它莱计算曲面积分
(7)会用曲积分和曲面积分求一些几何量与物理量
11、微分方程
(1)了解微分方程及其解、通解、初始条件和特解等概念
(2)掌握变量可分离的方程及一阶线性方程的解法
(3)会解齐次方程,伯努力方程和全微分方程,会用简单变量代换解某些微分方程
(4)会用降解法解下列方程:
(5)理解线性微分方程解的性质及解的结构定理
(6)掌握二阶常系数齐次线性微分方程的解法,并会解高于二阶的常系数齐次线性微分方程
(7)会求二阶常系数非齐次线性微分方程的特解
(8)会解二阶欧拉方程
(9)会用微分方程解一些简单的应用问题
上海大学插班生高等数学B基本要求
作者:
招考无忧 发布时间:
2008-07-2521:
27:
08 来源:
招考无忧
1、函数、极限、连续
(1)、理解函数的概念,掌握函数的表示方法
(2)了解函数的奇偶性、单调性、周期性和有界性
(3)理解复合函数的概念,了解反函数及隐函数的概念。
会建立简单函数关系式
(4)理解极限的概念,了解分段函数的极限
(5)掌握极限四则运算法则,掌握利用两个重要极限求极限的方法。
(6)理解无穷小、无穷大以及无穷小的阶的概念,会利用等价无穷小求极限1(7)理解函数连续性的概念,会判断函数间断点的类型
(8)了解初等函数的连续性和闭区间上的连续函数的性质,并会应用这些性质
2、导数与微分
(1)理解导数的概念导数的几何意义和物理意义,函数的可导性与连续性之间的关系
(2)掌握导数的四则元算法则和复合函数的求导法,掌握基本初等函数的导数公式。
会求分段函数的一阶二阶导数
(3)了解高阶函数的概念,会求简单的函数的n阶导数,掌握初等函数的二阶导数的求法
(4)会求隐函数和参数方程所确定的函数的一、二阶导数。
(5)了解微分的概念和四则运算
3、中值定理与导数的应用
(1)理解并会应用罗尔定理、拉格朗日定理,利用定理能求方程的根、证明不等式。
了解柯西定理
(2)理解函数的极值概念,掌握用导数判别函数的单调性和求函数极值的方法
(3)会用导数描绘图形
(4)会求MAX、MIN的应用问题
(5)掌握洛必达法则求未定式极限的方法
4、不定积分
(1)理解原函数的概念,理解不定积分的概念及性质
(2)掌握不定积分的基本公式、换元法、分部积分法
5、定积分及其应用
(1)理解定积分的基本概念,定积分的中值定理
(2)理解变限函数及其求导定理,掌握牛顿—莱布尼兹公式
(3)掌握定积分的性质及换元积分法和分部积分法
(4)会定积分计算一些几何量,会用定积分求解一些简单的经济应用题
(5)了解广义积分的概念、收敛与发散的概念,掌握计算广义积分的基本方法
6、微分方程与差分方程
(1)了解微分方程及其解、通解、初始条件和特解等概念
(2)掌握变量可分离的方程及一阶线性方程的解法
(3)会用降解法解下列方程:
(4)了解差分与差分方程及其通解与特解的概念
(5)理解线性微分方程解的性质及解的结构定理
(6)掌握二阶常系数齐次线性微分方程的解法
(7)会求二阶常系数非齐次线性微分方程的特解
(8)掌握一阶常系数线性差分方程的求解方法
(9)会用微分方程与差分方程解一些简单的经济应用问题
7、多元函数微分学
(1)理解多元函数的概念
(2)理解二元函数的极限与连续的概念
(3)理解偏导数于全微分的概念
(4)掌握复合函数一阶二阶偏导数的求法
(5)会求隐函数的偏导数
(6)理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘法求条件极值,会求简单多元含函数的最大值与最小值并会解决一些简单的应用问题
8、二重积分
(1)理解二重积分的概念,了解二重积分的性质
(2)掌握二重积分的计算方法
(3)会计算无界区域上较简单的二重积分
9、级数
(1)理解常数项级数收敛与发散的概念、收敛级数和的概念,掌握级数的基本性质及收敛的必要条件
(2)掌握几何级数、P—级数的收敛性
(3)掌握正向级数的判别法
(4)会用交错级数的莱布尼兹判别法
(5)了解无穷级数绝对收敛与条件收敛的概念,及两者之间的关系
(6)掌握幂级数的收敛半径,收敛区间及收敛域的求法
(7)了解幂级数在收敛区间内的一些基本性质,会求一些简单幂级数在收敛区间内的和函数,并会由此求出某些数的项级数的和
(8)了解泰勒公式、泰勒级数,掌握的麦克劳林展开式,会用它们将一些简单函数展开幂级数
华东理工大学2010年插班生招生学院和专业计划、体检限制、笔试科目
招生学院
专业名称及招生限数
最大招生数
体检限制
笔试科目
化工学院
国家重点学科
化学工程与工艺(4)
4
色弱,色盲,嗅觉迟钝
高等数学
(一),大学英语
(一),现代基础化学
生物工程学院
国家重点学科
生物工程
(2),生物技术
(1),生物科学
(1),食品科学与工程
(1),食品质量与安全
(1)
6
化学与分子工程学院
国家重点学科
化学
(1),应用化学
(2),应用化学(精细化工)
(2),材料化学
(1)
6
药学院
药学
(1),制药工程
(1),药物制剂
(1)
3
材料科学与工程学院
国家重点学科
高分子材料与工程(3),无机非金属材料工程
(1),复合材料与工程
(1),材料物理
(1),材料化学(材料制备)
(1)
7
资源与环境工程学院
环境工程
(2),热能与动力工程
(1)
3
色盲
信息科学与工程学院
自动化
(2),测控技术及仪器
(2),电气工程及其自动化
(2),信息工程
(2)
8
色盲
高等数学
(一),大学英语
(一),大学物理
机械与动力工程学院
国家重点学科
机械设计制造及其自动化
(2),过程装备与控制工程
(2)你的专业相同
4
理学院
数学与应用数学
(1),信息与计算科学
(1)
2
高等数学
(二),大学英语
(一)
商学院
价值=支付意愿=市场价格×消费量+消费者剩余国际经济与贸易
(2),金融学
(2),会计学
(2),财务管理
(2),物流管理
(2),工商管理
(2)
1.规划环境影响评价的报审12
考金融学就不用考物理
环境影响经济损益分析一般按以下四个步骤进行:
高等数学
(一),大学英语
(一)
笔试内容:
《大学英语
(一)》大纲
要求:
笔试+听力,考试内容及难度相当于大学英语国家四级水平要求。
在可行性研究时应进行安全预评价的建设项目有:
《大学英语
(二)》大纲
要求:
笔试+听力,考试内容及难度相当于大学英语国家六级水平要求。
(五)规划环境影响评价的跟踪评价 《高等数学
(一)》大纲
按照国家规定实行审批制的建设项目,建设单位应当在报送可行性研究报告前报批环境影响评价文件。
按照国家规定实行核准制的建设项目,建设单位应当在提交项目申请报告前报批环境影响评价文件。
按照国家规定实行备案制的建设项目,建设单位应当在办理备案手续后和开工前报批环境影响评价文件。
函数了解函数的性质。
理解复合函数和反函数的概念。
熟悉基本初等函数的性质及其图形。
3.划分评价单元 导数与极限掌握极限的性质和各种计算方法。
掌握导数的计算方法。
微分学的基本定理及导数的应用理解微分的概念及其几何意义,会计算微分。
会应用罗尔(Rolle)定理、拉格朗日定理、柯西(Cauchy)定理。
了解泰勒(Taylor)定理。
掌握导数的应用。
一元函数积分学理解定积分的概念、几何意义和性质。
理解变限积分函数及其求导定理。
掌握牛顿(Newton)—莱布尼兹(Leibniz)公式。
掌握不定积分、定积分的计算方法。
掌握建立定积分表达式的微元法。
无穷级数理解无穷级数概念及其基本性质。
了解级数绝对收敛和条件收敛的概念及其性质。
会利用幂级数性质求一些幂级数的和函数。
环境敏感区,是指依法设立的各级各类自然、文化保护地,以及对建设项目的某类污染因子或者生态影响因子特别敏感的区域。
微分方程会求解一阶方程中的可分离变量方程、齐次型方程、一阶线性方程、伯努里方程。
会利用变量代换方法求解微分方程。
会求解可降阶的高阶方程。
理解二阶线性微分方程解的结构。
掌握求解二阶线性常系数齐次、非齐次微分方程。
了解n阶线性常系数齐次微分方程的解法。
会应用微分方程解决一些简单的实际问题。
疾病成本法和人力资本法是用于估算环境变化造成的健康损失成本的主要方法,或者说是通过评价反映在人体健康上的环境价值的方法。
向量与空间解析几何掌握向量的运算。
掌握两个向量垂直、平行的条件以及夹角的求法。
掌握平面方程和直线方程的求法。
掌握常用二次曲面的方程及其图形。
了解旋转面、柱面、锥面的方程。
会求空间曲线在坐标面上的投影曲线方程。
多元函数微分学理解多元函数的概念。
会计算二元函数的极限。
会计算函数、隐函数(包括由方程组确定)的偏导数、二阶偏导数、全微分。
了解全微分存在的必要条件和充分条件。
了解一元向量值函数的导数计算方法。
会计算方向导数与梯度。
会计算曲线的切线与法平面及曲面的切平面与法线。
会求二元函数的极值。
会用拉格朗日乘数法求条件极值。
会求解一些最值的应用问题。
重积分理解二重积分的概念、性质。
熟练掌握二重积分的计算方法。
了解建立二重积分积分表达式的微元法。
会计算一些几何量与物理量。
参考书:
《高等数学(上、下)》,殷锡鸣主编,高等教育出版社
《高等数学(一元微积分)》、《高等数学(多元微积分)》,谢国瑞主编,华东理工大学出版社
《高等数学
(二)》大纲
专项规划工业、农业、畜牧业、林业、能源、水利、交通、城市建设、旅游、自然资源开发有关的专项规划。
环境影响报告书 函数、极限与导数了解函数及其性质。
掌握极限的性质和计算方法。
掌握无穷小的比较。
理解函数连续的概念。
会判断间断点的类型。
知道闭区间上连续函数的性质。
理解导数的概念、几何意义。
掌握导数的计算方法。
能熟练计算初等函数、隐函数、参数方程的一阶、二阶导数,会求一些简单函数的n阶导数。
会求曲线(包括极坐标下曲线)的切线与法线方程。
微分学的基本定理及导数的应用理解微分的概念及其几何意义,会计算微分。
会应用罗尔定理、拉格朗日定理、柯西定理。
了解泰勒(Taylor)定理。
掌握导数的应用。
一元函数积分学理解定积分的概念、几何意义和性质。
理解变限积分函数求导定理。
掌握牛顿(Newton)—莱布尼兹(Leibniz)公式。
掌握不定积分、定积分的计算方法。
掌握建立定积分表达式的微元法。
会计算一些几何量与物理量。
了解广义积分的概念及其计算方法。
无穷级数理解无穷级数概念及其基本性质。
了解正项级数的判别法。
了解交错级数的莱布尼兹判别法。
了解级数绝对收敛和条件收敛的概念及其性质。
掌握幂级数收敛域的求法。
会利用幂级数性质求一些幂级数的和函数。
会求数项级数的和。
会将一些简单的函数展开成幂级数。
微分方程会求解一阶方程中的可分离变量方程、齐次型方程、一阶线性方程、伯努里方程。
会利用变量代换方法求解微分方程。
会求解可降阶的高阶方程。
理解二阶线性微分方程解的结构。
掌握求解二阶线性常系数齐次、非齐次微分方程。
了解n阶线性常系数齐次微分方程的解法。
会应用微分方程解决一些简单的实际问题。
向量与空间解析几何掌握向量的运算。
掌握两个向量垂直、平行的条件以及夹角的求法。
掌握平面方程和直线方程的求法。
掌握常用二次曲面的方程及其图形。
了解旋转面、柱面、锥面的方程。
会求空间曲线在坐标面上的投影曲线方程。
多元函数微分学理解多元函数的概念。
会计算二元函数的极限。
了解连续性、有界闭域上连续函数的性质。
会计算函数、隐函数(包括由方程组确定)的偏导数、二阶偏导数、全微分。
了解全微分存在的必要条件和充分条件。
了解一元向量值函数的导数计算方法。
会计算方向导数与梯度。
会计算曲线的切线与法平面及曲面的切平面与法线。
会求二元函数的极值。
会用拉格朗日乘数法求条件极值。
会求解一些最值的应用问题。
重积分理解二重积分、三重积分的概念、性质。
熟练掌握二重积分的计算方法。
掌握三重积分的计算方法。
了解建立重积分表达式的微元法。
会计算一些几何量与物理量。
第一型曲线积分与曲面积分理解第一型曲线积分、曲面积分的概念、性质。
会计算第一型曲线积分和曲面积分。
了解建立第一型曲线积分和曲面积分表达式的微元法。
会计算一些几何量与物理量
第二型曲线积分与曲面积分理解第二型曲线积分、曲面积分的概念、性质。
了解两类曲线和曲面积分的关系。
会计算第二型曲线积分和曲面积分。
掌握格林(Green)公式。
会运用平面和空间第二型曲线积分与路径无关的条件计算曲线积分。
了解高斯(Gauss)公式,斯托克斯(Stokes)公式。
会计算散度、旋度。
了解无旋场、无散度场的曲线、曲面积分的性质。
了解建立第二型曲线积分和曲面积分表达式的微元法。
会计算一些物理量。
傅里叶级数了解用三角函数逼近周期函数的思想。
了解函数展开为傅里叶(Fourier)级数的狄利克雷(Dirichlet)定理。
会将周期函数以及定义在有限区间上的函数展开为傅里叶级数。
会将定义在[0,]上的函数展开为正弦或余弦级数。
参考书:
《高等数学(上、下)》,殷锡鸣主编,高等教育出版社
《高等数学(一元微积分)》、《高等数学(多元微积分)》,谢国瑞主编,华东理工大学出版社
《大学物理》大纲
力学质点运动的描述、相对运动;牛顿运动定律及其应用、变力作用下的质点动力学基本问题;非惯性系和惯性力;质点与质点系的动量定理和动量守恒定律;质心、质心运动定理;变力的功、动能定理、保守力的功、势能、机械能守恒定律;刚体定轴转动定律、转动惯量;刚体转动中的功和能;质点、刚体的角动量、角动量守恒定律。
热学平衡态、态参量、热力学第零定律;理想气体状态方程;准静态过程、热量和内能;热力学第一定律、典型的热力学过程;多方过程;循环过程、卡诺循环、热机效率、致冷系数;热力学第二定律、熵和熵增加原理、玻尔兹曼熵关系式;统计规律、理想气体的压强和温度;理想气体的内能、能量按自由度均分定理;麦克斯韦速率分布律、三种统计速率;玻耳兹曼分布;气体分子的平均碰撞频率和平均自由程。
静电场库仑定律、电场强度、电场强度叠加原理及其应用;静电场的高斯定理;电势、电势叠加原理;电场强度和电势的关系、静电场的环路定理;导体的静电平衡;电介质的极化及其描述;有电介质存在时的电场;电容。
参考书:
《大学物理》上册(第二版),戴坚舟、钱水兔、阴其俊、汪溶,华东理工大学出版社
《大学物理》下册(第二版),戴坚舟、钱水兔、阴其俊、汪溶,华东理工大学出版社
《普通物理学》第1、2册(第五版),程守洙、江之永,高等教育出版社
《大学物理学》第一、二、三册力学、热学、电磁学(第二版),张三慧,清华大学出版社
《现代基础化学》大纲
原子结构和元素周期系四个量子数,s,p,d原子轨道角度分布图和电子云的角度分布图,原子核外电子排布与元素周期系,原子结构与元素性质的关系。
分子结构和分子间力、氢键共价键的形成及类型,杂化轨道理论及物质的空间构型判断。
分子间力类型及氢键对物质性质的影响。
理想气体状态方程及其计算
化学反应热力学
(1)热力学基本概念,热力学第一定律,利用生成热,燃烧热,相变热及Hess定律进行化学反应热效应计算。
(2)化学反应的方向和化学平衡,吉氏函数概念及其计算,化学平衡常数概念,化学平衡的计算和化学平衡的移动。
化学反应动力学化学反应速率的定义,反应速率方程及其相关计算。
酸碱平衡酸碱质子理论内容,弱酸弱碱的解离平衡概念及计算,缓冲溶液概念