初中数学 中考模拟数学总复习图形的对称经典考试题及答案1.docx
《初中数学 中考模拟数学总复习图形的对称经典考试题及答案1.docx》由会员分享,可在线阅读,更多相关《初中数学 中考模拟数学总复习图形的对称经典考试题及答案1.docx(17页珍藏版)》请在冰豆网上搜索。
初中数学中考模拟数学总复习图形的对称经典考试题及答案1
xx学校xx学年xx学期xx试卷
姓名:
_____________年级:
____________学号:
______________
题型
选择题
填空题
简答题
xx题
xx题
xx题
总分
得分
评卷人
得分
一、xx题
(每空xx分,共xx分)
试题1:
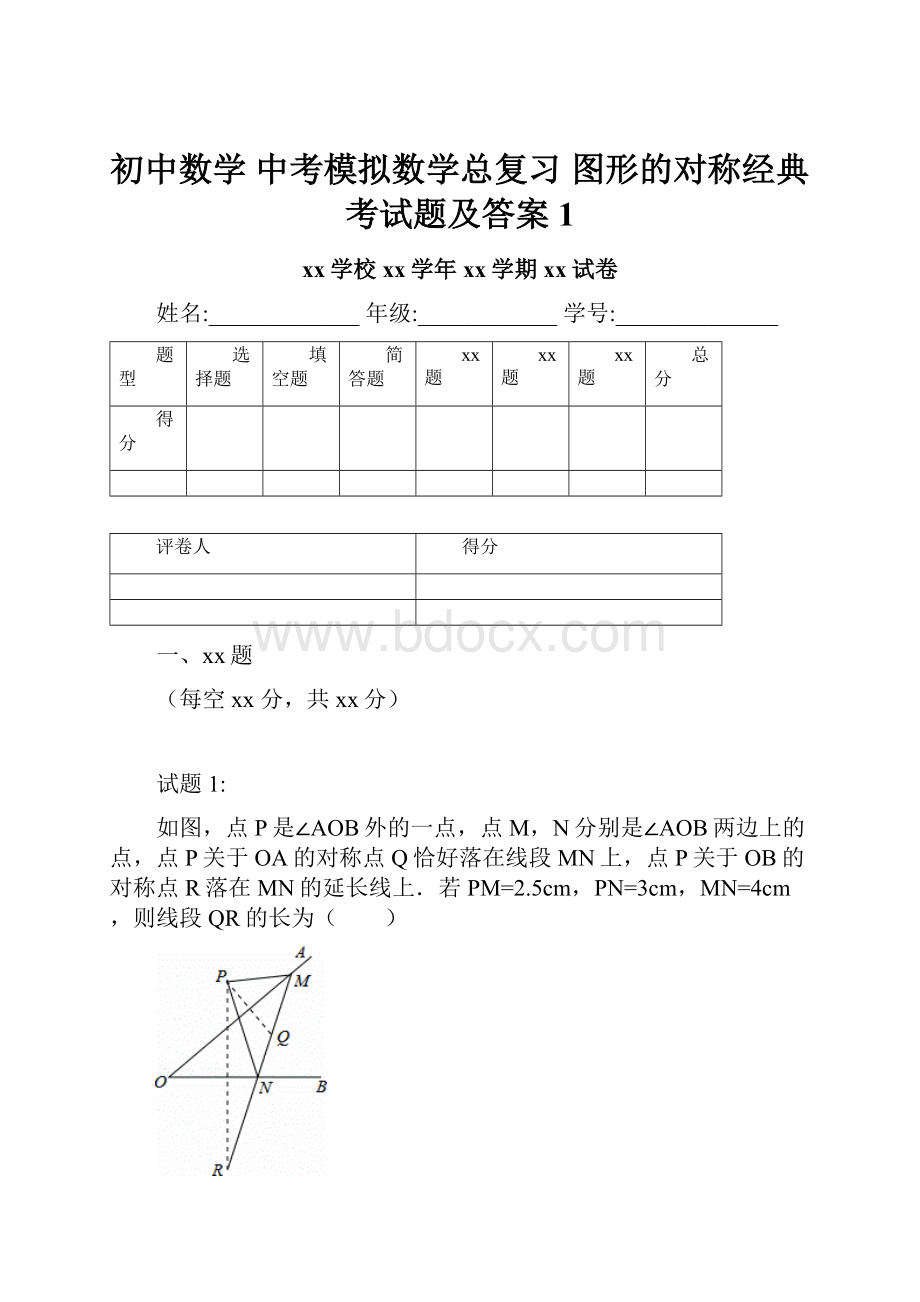
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
A. 4.5 B.5.5 C.6.5 D.7
试题2:
如图,直角坐标系中的五角星关于y轴对称的图形在( )
A. 第一象限 B第二象限 C.第三象限 D.第四象限
试题3:
下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A. 1 B.2 C3D. 4
试题4:
下面几何图形中,一定是轴对称图形的有( )
A. 1个 B.2个 C.3个 D.4个
试题5:
点A(1,﹣2)关于x轴对称的点的坐标是( )
A. (1,﹣2) B.(﹣1,2) C(﹣1,﹣2) D.(1,2)
试题6:
点P(2,﹣5)关于x轴对称的点的坐标为( )
A. (﹣2,5) B(2,5) C.(﹣2,﹣5) D.(2,﹣5)
试题7:
在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )
A. (3,2) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
试题8:
已知点A(a,2013)与点B(2014,b)关于x轴对称,则a+b的值为( )
A. ﹣1 B.1 C.2 D.3
试题9:
(将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )
A.
B
C.
D.
试题10:
如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是 .
试题11:
点P(﹣2,3)关于x轴的对称点P′的坐标为
试题12:
点P(2,3)关于x轴的对称点的坐标为 .
试题13:
若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n= .
试题14:
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 种.
试题15:
如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
试题16:
在平面直角坐标系中,已知点A(﹣3,1),B(﹣1,0),C(﹣2,﹣
1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.
试题17:
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点,点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
试题18:
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:
△ADE≌△CED;
(2)求证:
DE∥AC.
试题19:
如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:
△EDF≌△CBF;
(2)求∠EBC.
试题20:
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
(1)求证:
△AOE≌△COD;
(2)若∠OCD=30°,AB=
,求△AOC的面积.
试题21:
准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:
四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
试题1答案:
A 解:
∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的
延长线上,
∴PM=MQ,PN=NR,
∵PM=2.5cm,PN=3cm,MN=4cm,
∴RN=3cm,MQ=2.5cm,
即NQ=MN﹣MQ=4﹣2.5=1.5(cm),
则线段QR的长为:
RN+NQ=3+1.5=4.5(cm).
试题2答案:
A 解:
如图所示,直角坐标系中的五角星关于y轴对称的图形在第一象限.
故选:
A.
试题3答案:
C 解:
第一个是轴对称图形,有2条对称轴;
第二个是轴对称图形,有2条对称轴;
第三个是轴对称图形,有2条对称轴;
第四个是轴对称图形,有3条对称轴;
∴对称轴的条数为2的图形的个数是3;
试题4答案:
C 解:
圆弧、角、等腰梯形都是轴对称图形.
试题5答案:
D 解:
点A(1,﹣2)关于x轴对称的点的坐标是(1,2),
试题6答案:
B 解:
∵点P(2,﹣5)关于x轴对称,
∴对称点的坐标为:
(2,5).
试题7答案:
B 解:
∵点A(2,3),
∴点A关于x轴的对称点的
坐标为:
(2,﹣3).
试题8答案:
B 解:
∵A(a,2013)与点B(
2014,b)关于x轴对称,
∴a=2014,b=﹣2013
∴a+b=1,
试题9答案:
B 解:
严格按照图中的顺序向右上翻折,向左上角翻折,剪去左上角,展开得到结论.
试题10答案:
2
解:
作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2
,
即DQ+PQ的最小值为2
,
故答案为:
2
.
试题11答案:
(﹣2,﹣3) .
解:
∵点P(﹣2,3)关于x轴的对称点P′,
∴点P′的横坐标不变,为﹣2;纵坐标为﹣3,
∴点P关于x轴的对称点P′的坐标为(﹣2,﹣3).
试题12答案:
(2,﹣3) 解:
∵点P(2,3)
∴关于x轴的对称点的坐标为:
(2,﹣3).
故答案为:
(2,﹣3).
点评:
此题主要考查了关于x轴、y轴对称点的性质,正确记忆坐标规律是解题关键.
13.点P(1,﹣2)关于y轴对称的点的坐标为 (﹣1,﹣2) .
考点:
关于x轴、y轴对称的点的坐标.
专题:
常规题型.
分析:
根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答即可.
解答:
解:
点P(1,﹣2)关于y轴对称的点的坐标为(﹣1,﹣2).
试题13答案:
0 解:
∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,3=n+5,
解得:
m=2,n=﹣2,
∴m+n=0,
试题14答案:
3 解:
在1,2,3处分别涂黑都可得一个轴对称图形,
故涂法有3种,
故答案为:
3.
试题15答案:
5 解:
作M关于BD的对称点Q,连接NQ,
交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=
AC=3,BP=
BD=4,
在Rt△BPC中,由勾股定理得:
BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:
5.
试题16答案:
解:
如图所示:
△DEF与△ABC关于y轴对称的图形.
试题17答案:
解:
(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)点B关于x轴的对称点B′的坐标为(0,﹣3),
由轴对称确定最短路线问题,连接AB′与x轴的交点即为点P,
设直线AB′的解析式为y=kx+b(k≠0),
则
,
解得
,
∴直线AB′的解析式为y=7x﹣3,
令y=0,则7x﹣3=0,
解得x=
,
所以,当PA+PB的值最小时的点P的坐标为(
,0).
试题18答案:
证明:
(1)∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
又∵AC是折痕,
∴BC=CE=AD,
AB=AE=CD,
在△ADE与△CED中,
,
∴△ADE≌△CED(SSS);
(2)∵△ADE≌△CED,
∴∠EDC=∠DEA,
又∵△ACE与△ACB关于AC所在直线对称,
∴∠OAC=∠CAB,
∵∠OCA=∠CAB,
∴∠OAC=∠OCA,
∴2∠OAC=2∠DEA,
∴∠OAC=∠DEA,
∴DE∥AC.
试题19答案:
(1)证明:
由折叠的性质可得:
DE=BC,∠E=∠C=90°,
在△DEF和△BCF中,
,
∴△DEF≌△BCF(AAS
);
(2)解:
在Rt△ABD中,
∵AD=3,BD=6,
∴∠ABD=30°,
由折叠的性质可得;∠DBE=∠ABD=30°,
∴∠EBC=90°﹣30°﹣30°=30°.
试题20答案:
(1)证明:
∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°,
∵矩形ABCD沿对角线AC折叠点B落在点E处,
∴AB=AE,∠B=∠E,
∴AE=CD,∠D=∠E,
在△AOE和△COD中,
,
∴△AOE≌△COD(AAS);
(2)解:
∵△AOE≌△COD,
∴AO=CO,
∵∠OCD=30°,AB=
,
∴CO=CD÷cos30°=
÷
=2,
∴△AOC的面积=
AO•CD=
×2×
=
.
试题21答案:
(1)证明:
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴∠EBD=
∠ABD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形.
(2)解:
∵四边形BFDE为菱形,
∴BE=ED,∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=90°,
∴∠ABE=30°,
∵∠A=90°,AB=2,
∴AE=
=
,BF=BE=2AE=
,
故菱形BFDE的面积为:
×2=
.