考研机械凸轮典型计算例题.docx

考研机械凸轮典型计算例题.docx

《考研机械凸轮典型计算例题.docx》由会员分享，可在线阅读，更多相关《考研机械凸轮典型计算例题.docx（14页珍藏版）》请在冰豆网上搜索。

考研机械凸轮典型计算例题

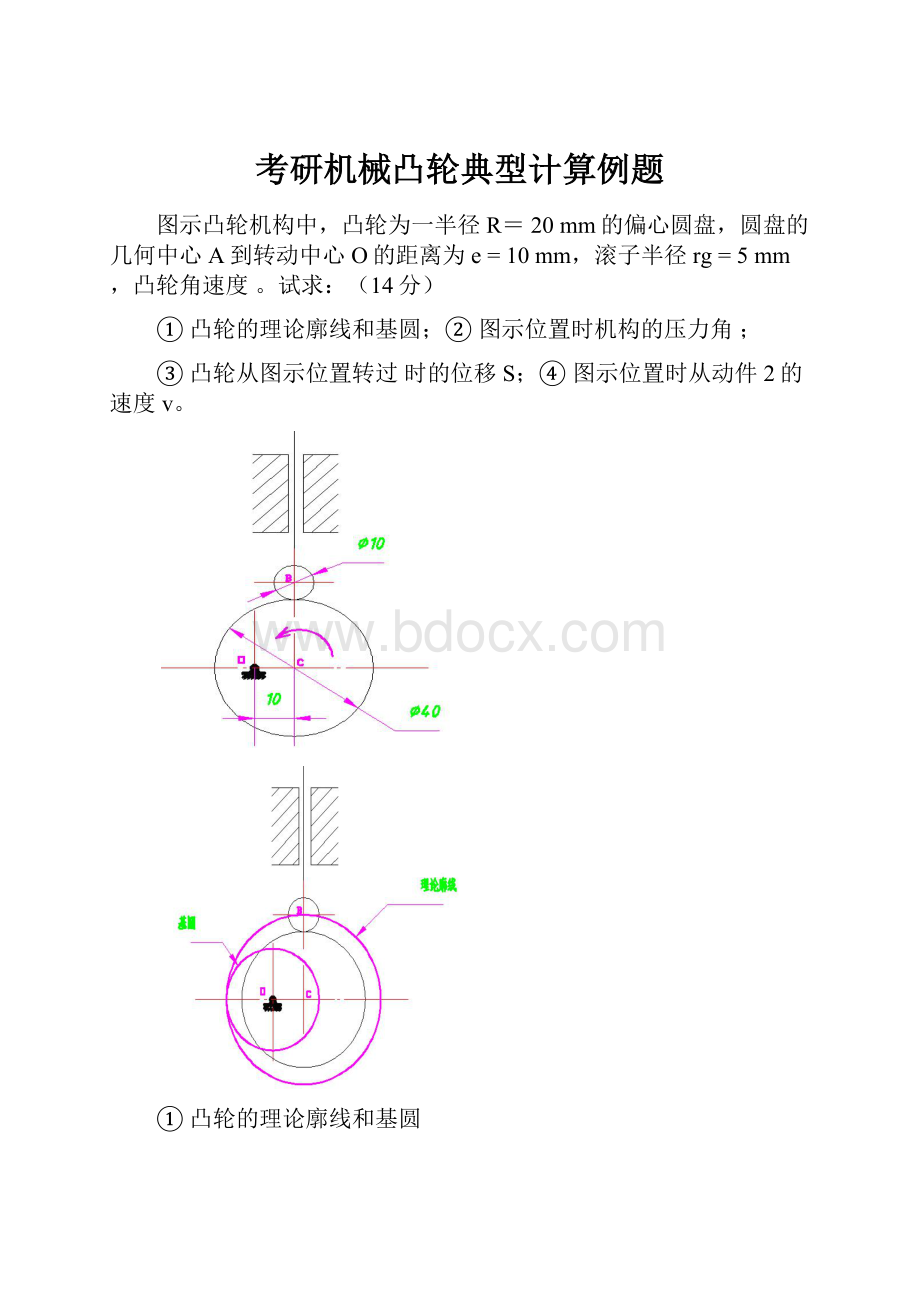
图示凸轮机构中，凸轮为一半径R＝ 20mm的偏心圆盘，圆盘的几何中心A到转动中心O的距离为e =10mm，滚子半径rg =5mm，凸轮角速度 。

试求：

（14分）

① 凸轮的理论廓线和基圆；② 图示位置时机构的压力角 ；

③ 凸轮从图示位置转过 时的位移S；④ 图示位置时从动件2的速度v。

① 凸轮的理论廓线和基圆

       理论廓线。

对于滚子推杆的凸轮机构而言，理论廓线是过滚子中心的一条封闭廓线。

题目中给出的是工作廓线，要得到理论廓线，只需要把工作廓线往外偏移一个滚子的半径即可。

由于这里工作廓线就是一个以C为圆心，半径为20mm的圆；而滚子的半径是5mm，所以理论廓线就是以C为圆心，半径为20+5=25mm的圆.如下图所示。

       基圆。

首先我们知道，基圆是在理论廓线上定义的；其次我们懂得，它是以转动中心O为圆心的，与理论廓线内切的一个半径最小的圆。

按照该定义，我们以O为圆心做一个与理论廓线内切的最小的圆如下图，显然，它的半径是10+5=15mm.

② 图示位置时机构的压力角 ；

       对于该机构而言，压力角是滚子的中心B点的受力方向与运动方向的夹角。

       B点的速度方向。

由于B点是推杆与滚子的连接点，所以它也就是推杆上的B点。

由于推杆在上下平移，推杆上任何一点的轨迹都是沿着推杆的直线，所以任何一点的速度方向都是推杆直线的方向，因此推杆上的B点速度方向也在该直线上。

：

       B点的受力方向。

推杆上的B点与理论廓线接触，在忽略摩擦的前提下，其受力方向其实就是理论力学中的光滑接触面中的反力方向。

光滑接触面的反力是公法线方向。

由于推杆的B点是尖点，无所谓法线，所以公法线方向就是理论廓线在该点的法线方向。

而理论廓线是一个圆，圆上任何一点的法线方向都是从从该点指向圆心的。

所以BC的方向就是公法线方向。

       显然，速度方向与力的方向重合，所以压力角是0度。

这是我们最希望的压力角。

压力角越小，则凸轮机构的传力性能越好。

③ 凸轮从图示位置转过 时的位移S；

       对于这种问题，总是用反转法通过作图测量出来的。

       使用反转法，我们给整个凸轮机构（包括机架）一个与凸轮转向相反，速度相同的角速度，从而使得凸轮静止，而机架围绕凸轮的转动中心转动，此时，推杆会一方面跟随机架转动，另外，又相对机架做平移。

按照理论力学的说法，若取机架为动系，则推杆在做一个牵连运动为定轴转动，而相对运动为平移运动的平面运动。

       当推杆发生这样的平面运动时，在作图中，实际上是一个三角形在发生定轴转动，认识这一点非常重要。

下面稍微详细的描述此问题。

       首先做出偏距圆和基圆。

按照前面的方法，基圆已经做出；而偏距圆是以O为圆心，与推杆的导路相切的一个圆，如下图所示。

 确定转动三角形的初始位置。

推杆的导路与偏距圆的切点为C点，而推杆的导路与基圆在上面的交点为D点。

连接OCD得到一个三角形如图。

则用反转法设计凸轮时，实际上就是该三角形在定轴转动，抓住这个核心很重要。

       在本问题中问到，凸轮从图示位置转过 时的位移S是多少首先要确定的是，转过90度后，推杆的导路在哪里转过90度，就是三角形ODC逆时针转了90度，也就是OC逆时针转了90度，或者是OD转了90度。

一般而言，用OC转了90度更好说明问题。

所以做C’0C，使得其夹角为90度，然后从C’点做一条直线与偏距圆相切，则该直线就是此时推杆所处的导路。

该导路与基圆相交的点为D’。

则OC’D’就是转动90度后的三角形。

。

要确定转过90度后的位移，首先我们回忆一下，在任何一个时刻推杆的位移是如何度量的实际上，推杆的位移都是在推杆的导路上度量的。

推杆的导路与基圆和理论廓线分别由两个交点，这两个交点之间的距离就是推杆相对于近休点的位移。

所以在图中，初始位置处BD的距离是题目状态下推杆相对于近休点的位移；而B’D’是转动90度后推杆相对于近休点的位移；测量这两个位移，然后取它们的差，就是转动90度后推杆所发生的相对位移，经测量，此位移是。

④ 图示位置时从动件2的速度v。

       求推杆的速度，实际上是理论力学中的运动分析问题。

，由于推杆和凸轮之间是高副，所以需要使用合成运动的分析方法，取动点，动系，并使用速度合成定理来解决。

       上述方法固然不错，不过还有另外一种更快捷的方法，也就是机械原理里面力推的瞬心法。

只要我们能够找到凸轮和推杆的相对速度瞬心，由于凸轮是定轴转动，则我们会很容易得到此瞬心的速度，这样就马上得到了推杆上该瞬心的速度。

由于推杆在平移，上面任何一点速度相同，所以我们立刻就得到了推杆的速度。

这样，寻找相对速度瞬心就成为关键。

       首先去掉滚子，画出理论廓线。

下面要求推杆2和凸轮1的相对瞬心。

       由于推杆2和凸轮1是平面高副连接，所以其相对瞬心应该在接触点的公法线上，也就是在过B点的竖直线BC上，但是在这根线的什么地方呢

       要确定具体的地方，需要使用三心定理。

三心定理说，三个做相对平面运动的物体有三个相对速度瞬心，这三个瞬心一定在一条直线上。

       要使用三心定理，需要确定三个做相对运动的构件，这三个构件中要包含我们需要分析的两个构件。

这里，除了凸轮1和推杆2，只有机架3了，因此我们取这三个构件来应用三心定理。

       凸轮1和推杆2的瞬心是要求的；而凸轮1和机架3的瞬心在O点；推杆2和机架的瞬心在垂直于导路的无穷远处。

那么按照三心定理，凸轮1和推杆2的瞬心必然在过O点而与导路垂直的无穷远处，也就是在OC这条直线上。

       这样，瞬心既在BC上，又在OC上，而这两根线相交于C点，所以C点就是相对速度瞬心。

    既然如此，我们求出凸轮上C点的速度，它也同时就是推杆上C点的速度，而推杆因为在平移，所以它也就是推杆的速度。

&

       凸轮在定轴转动，其上面C点的速度是

则推杆的速度就是10mm/s.

  至此，该问题就全部解完了

用齿条型刀具范成法加工一个渐开线直齿圆柱齿轮，设已知被加工齿轮轮坯的角速度

=5rad/s，刀具移动速度为

=m/s，刀具的模数m =10mm，压力角

=

。

试求：

2被加工齿轮的齿数z1。

②若齿条分度线与被加工齿轮中心的距离L＝77mm，则被加工齿轮是否为变位齿轮若是，则其变位系数x为多少

③若已知该齿轮与另一大齿轮2相啮合时的传动比

＝4，两齿轮的中心距为377mm，求这两个齿轮的节圆半径

、

及啮合角

。

【

【问题求解】

①被加工齿轮的齿数z1。

首先根据加工条件确定齿轮的分度圆半径。

在用齿条刀具进行范成法加工时，齿条型刀具的分度线必须与被加工齿轮的分度圆相切并做纯滚动，而啮合点是节点，该节点的速度是s，从而轮坯上该点的速度为s。

由于轮坯在做定轴转动，其角速度已知

=5rad/s，根据定轴转动刚体上任何一点的速度与角速度关系

此即齿轮的分度圆半径。

这样，被加工齿轮的齿数是

显然，齿数15小于不发生根切的临界齿数17.这意味着，如果用标准方法加工的话，该齿轮会发生根切。

②若齿条分度线与被加工齿轮中心的距离L＝77mm，则被加工齿轮是否为变位齿轮若是，则其变位系数x为多少

从第一步计算知道，在标准加工时，齿条分度线与被加工齿轮中心的距离是75mm,会发生根切。

【

而这里给出距离是77mm，就是说齿条刀具远离了标准位置，这是在进行正变位加工，所以加工出来的齿轮就是正变位齿轮。

变位系数的计算

③若已知该齿轮与另一大齿轮2相啮合时的传动比

＝4，两齿轮的中心距为377mm，求这两个齿轮的节圆半径

、

及啮合角

。

（1）根据传动比计算出另外一个齿轮的齿数。

无论齿轮是标准齿轮还是变位齿轮，都属于渐开线齿轮。

渐开线齿轮在啮合传动时，啮合点都是在两个齿轮的基圆的内公切线上移动，据此可以确定两个齿轮的传动比与基圆半径成反比，从而也与分度圆半径成反比，因为模数相等，所以也与齿数成反比。

这就是说，无论是否变位，都有传动比公式

（2）接下来求啮合角。

首先求出标准安装时候的中心距。

然后根据标准安装的中心距与非标准安装的中心距的关系式得到此时的啮合角。

（3）求两个齿轮的节圆半径。

直接代公式计算齿轮1的节圆半径，再根据中心距计算齿轮2的节圆半径。

该图表达了非标准安装时两个齿轮中一些几何要素的关系。

首先，每个齿轮给出了三个圆：

基圆，分度圆和节圆。

这里是非标准安装，所以每个齿轮的节圆和分度圆并不重合，成为两个圆。

首先要注意上图中的啮合线。

它是两个基圆的内公切线。

&

接着，注意啮合点P。

它是内公切线与两齿轮连心线的交点。

而后，齿轮1节圆的形成。

就是以O1为圆心，以节点P到01的距离为半径，形成一个圆。

齿轮2的节圆也是如此。

根据这两个节圆形成的定义，可以知道，两个齿轮的节圆是在啮合传动中形成的，没有啮合，就没有节点；没有节点，就谈不上节圆。

而且可以知道，节圆总是相切的。

最后，注意啮合角。

它是内公切线与节点P的速度方向的夹角。

在明确上面几个概念以后，要密切注意两个三角形。

即O1N1P和O2N2P,这是两个相似三角形。

无论齿轮怎么安装，这两个三角形总相似。

所以，可以知道两个齿轮的传动比

这就是第三问中说的，无论是否变位齿轮，也无论怎么安装，只要是渐开线齿轮传动，传动比公式

恒满足。

至于求啮合角和求节圆半径，都是根据该图来确定的。

所以希望大家务必仔细领会此图。

例    在图示轮系中，已知蜗轮1的头数z1=1，右旋；其它各轮齿数为：

z2=64，z2’= z4’=30，z3=z5=20，z4=70；蜗杆转速n1=1280r/min，圆锥齿轮5的转速n5=300r/min，转向如图所示。

试确定构件H的转速nH的大小和方向。

~

【问题分析】

首先分析轮系的构成。

可以看到蜗杆1与蜗轮2啮合传动，蜗轮2与齿轮2’同轴，蜗轮2’与齿轮3外啮合传动，齿轮3与齿轮4内啮合传动，而齿轮4与齿轮4’同轴，齿轮4’与锥齿轮5啮合传动。

在上述齿轮中，只有齿轮3的轴并非固定，其轴即是系杆H。

所以齿轮3是行星轮，与它啮合的齿轮2’,齿轮4是太阳轮。

从而，系杆H，齿轮3，齿轮2’和齿轮4这四个构件组成了一个周转轮系。

在划出周转轮系以后，剩下的部分，左边齿轮5和4’是定轴轮系；而右边的蜗杆2和蜗轮1是定轴轮系。

该问题已知齿轮5的转速和蜗杆转速，要求系杆H的转速。

这样求解思路应该是从两边往中间移动。

即

（1）对于定轴轮系5-4’，根据齿轮5的速度求出齿轮4’的转速，也就得到了齿轮4的转速。

（2）对于定轴轮系1-2，根据蜗杆的转速求出蜗轮2的转速，也就得到了齿轮2’的转速。

|

（3）对于周转轮系4-3-2’，使用反转法变成定轴轮系，然后根据从齿轮4-3-2’的传动比，推算系杆H的角速度。

由于齿轮转动方向的判断十分重要，所以对于每个轮系，在计算的时候，要高度注意方向的问题。

【问题求解】

（1）得到齿轮4’的转速。

首先绘出齿轮4’的转向。

这样，齿轮4’的转速是这也是齿轮4的转速。

（2）得到蜗杆2的转速。

首先绘出蜗轮2的转向。

由于是右旋蜗杆，用右手判断，从而可以给出蜗轮2的转向。

这样，蜗轮2的转速是

这也是齿轮2’的转速。

`

（3）把中间的周转轮系转化为定轴轮系，计算系杆H的转速。

把中间的周转轮系施加一个与系杆H反向的转动，使得系杆静止，从而转变成为定轴轮系。

设齿轮4的转向为正方向，则按照定义式，此转化轮系中的传动比

而按照定轴轮系的传动比，又有

请注意上式中的负号。

从4-3是内啮合，从3-2’是外啮合。

因为有一次外啮合，所以负号改变一次。

如果忽略了这里负号的判断，则很容易出现计算错误。

上述二式相等，有

此即系杆的转速，它与齿轮4’的转向相同。