带电粒子在匀强电场中的运动doc.docx

带电粒子在匀强电场中的运动doc.docx

《带电粒子在匀强电场中的运动doc.docx》由会员分享，可在线阅读，更多相关《带电粒子在匀强电场中的运动doc.docx（45页珍藏版）》请在冰豆网上搜索。

带电粒子在匀强电场中的运动doc

带电粒子在匀强电场中的运动

一、单项选择题

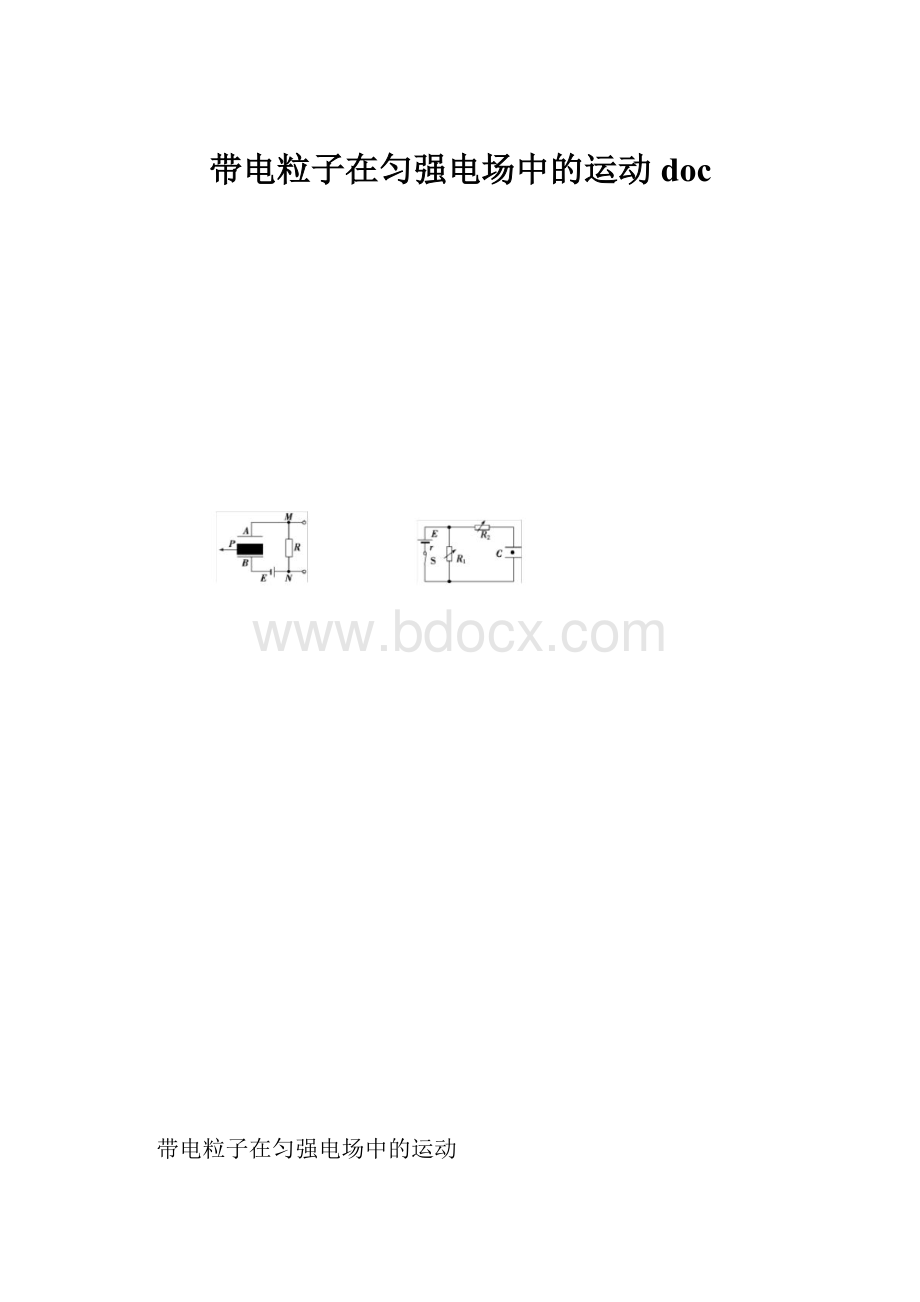
1.某位移式传感器的原理示意图如图所示，E为电源，R为电阻，平行金属板A、B和介质P构成

电容器，当可移动介质P向左匀速移出的过程中（）

A．电容器的电容变大B．电容器的电荷量保持不变

C．M点的电势比N点的电势低D．流过电阻R的电流方向从M到N

（第1题）（第2题）

2．如图所示，电路中R1、R2均为可变电阻，电源内阻不能忽略，平行板电容器C的极板水平放

置．闭合电键S，电路达到稳定时，带电油滴悬浮在两板之间静止不动．如果仅改变下列某—个条件，

油滴仍能静止不动的是（）

A．增大R1的阻值B．增大R2的阻值

C．增大两板间的距离D．断开电键S

3．如图所示，带电粒子P所带的电荷量是带电粒子Q的3倍，它们以相等的速度v0从同一点出

发，沿着跟电场强度垂直的方向射入匀强电场，分别打在M、N点，若OM＝MN，则P和Q的质量之

比为（粒子重力不计）（）

A．3∶4B．4∶3C．3∶2D．2∶3

（第3题）（第4题）

4.如图所示，

A、B两金属板平行放置，在

t＝0时将电子从

A板附近由静止释放

（电子的重力忽略

不计）．分别在

A、B两板间加上下列哪种电压时，有可能使电子到不了

B板（

）

5．如图所示，两平行金属板之间有一匀强电场，金属板长为L，一带电粒子以速度v0垂直于场强

方向沿上极板边缘射入匀强电场，刚好贴下极板边缘飞出，如果带电粒子以某一垂直于场强方向的初

速度v1沿上极板边缘射入电场并能从其中射出，当它的竖直位移等于板间距

d时，它的水平射程为

2L（轨迹未画出）．则粒子进入电场的初速度

v1等于（）

A．v

B．2v

0

v

0

D．2v

0

0

6．如图所示，在xOy竖直平面内存在着水平向右的匀强电场．有一带正电的小球自坐标原点沿

着y轴正方向以初速度v0抛出，运动轨迹最高点为M，与x轴交点为N，不计空气阻力，则小球（）

A．做匀加速运动B．从O到M的过程动能增大

C．到M点时的动能为零

1

2

D．到N点时的动能大于2mv

0

（第6题）（第7题）

7．如图所示，设两极板正对面积为S，极板间的距离为d，静电计指针偏角为θ.实验中，极板所

带电荷量不变，若（）

A．保持S不变，增大d，则θ变大B．保持S不变，增大d，则θ变小

C．保持d不变，减小S，则θ变小D．保持d不变，减小S，则θ不变

8．如图所示，平行金属板A、B水平正对放置，分别带等量异号电荷．一带电微粒水平射入板间，

在重力和电场力共同作用下运动，轨迹如图中虚线所示，那么（）

A．若微粒带正电荷，则A板一定带正电荷

B．微粒从M点运动到N点电势能一定增加

C．微粒从M点运动到N点动能一定增加

D．微粒从M点运动到N点机械能一定增加

（第8题）（第9题）

9．如图所示，从炽热的金属丝漂出的电子（速度可视为零），经加速电场加速后从两极板中间垂直

射入偏转电场．电子的重力不计．在满足电子能射出偏转电场的条件下．下述四种情况中，一定能使

电子的偏转角变大的是（）

A．仅将偏转电场极性对调

B．仅增大偏转电极间的距离

C．仅增大偏转电极间的电压

D．仅减小偏转电极间的电压

10.如图所示，竖直放置的两个平行金属板间存在匀强电场，与两板上边缘等高处有两个质量相同

的带电小球，P小球从紧靠左极板处由静止开始释放，Q小球从两板正中央由静止开始释放，两小球

最终都能运动到右极板上的同一位置，则从开始释放到运动到右极板的过程中它们的（）

A．运行时间tP>tQB．电势能减少量之比EP∶ΔEQ＝2∶1

C．电荷量之比qP∶qQ＝2∶1D．动能增加量之比EkP∶ΔEkQ＝4∶1

（第10题）（第11题）

11.有一静电场，其电势随x坐标的改变而改变，变化的图线如图所示．若将一带负电的粒子（重

力不计）从坐标原点O由静止释放，电场中P、Q两点分别位于x坐标轴上的1mm、4mm处．则下列

说法正确的是（）

A．粒子将沿x轴正方向一直向前运动

B．粒子在P点与Q点的加速度大小相等、方向相反

C．粒子经过P点与Q点时，动能相等

D．粒子经过P点与Q点时，电场力做功的功率相等

二、多项选择题

12.给平行板电容器充电，断开电源后A极板带正电，B极板带负电．板间一带电小球C用绝缘细

线悬挂，如图所示．小球静止时与竖直方向的夹角为θ，则（）

A．若将B极板向右平移稍许，电容器的电容将减小

B．若将B极板向下平移稍许，A、B两板间电势差将增大

C．若将B极板向上平移稍许，夹角θ将变大

D．轻轻将细线剪断，小球将做斜抛运动

（第12题）（第13题）

13．在地面附近，存在着一有界电场，边界MN将某空间分成上下两个区域Ⅰ、Ⅱ，在区域Ⅱ中

有竖直向上的匀强电场，在区域Ⅰ中离边界某一高度由静止释放一质量为m的带电小球A，如图甲所

示，小球运动的v－t图象如图乙所示，已知重力加速度为g，不计空气阻力，则（）

A．在t＝s时，小球经过边界MN

B．小球受到的重力与电场力之比为3∶5

C．在小球向下运动的整个过程中，重力做的功与电场力做的功大小相等

D．在小球运动的整个过程中，小球的机械能与电势能总和先变大再变小

14.如图所示，在两条竖直边界线所围的匀强电场中，一个不计重力的带电粒子从左边界的P点以

某一水平速度射入电场，从右边界的Q点射出，下列判断正确的有（）

A．粒子带正电

B．粒子做匀速圆周运动

C．粒子电势能增大

D．仅增大电场强度，粒子通过电场的时间不变

（第14题）（第15题）

15．如图所示，两对金属板A、B和C、D分别竖直和水平放置，A、B接在电路中，C、D板间电

压为板上O处发出的电子经加速后，水平射入C、D板间，电子最终都能打在光屏M上．关于电子的

运动，下列说法正确的是（）

A．S闭合，只向右移动滑片P，P越靠近b端，电子打在M上的位置越高

B．S闭合，只改变A、B板间的距离，改变前后，电子由O至M经历的时间相同

C．S闭合，只改变A、B板间的距离，改变前后，电子到达M前瞬间的动能相同

D．S闭合后再断开，只向左平移B，B越靠近A板，电子打在M上的位置越高

16.如图所示，水平放置的两平行金属板与一直流电源相连，一带正电的粒子仅在重力和电场力作

用下以某一初速度沿图中直线从A运动到B，现将平行金属板分别以O、O′为圆心在平面内旋转相同

角度后（角度不太大），粒子仍以原来的方式射入，则（）

A．粒子将做曲线运动

B．粒子仍做匀速直线运动

C．粒子做匀变速直线运动

D．粒子的电势能可能增加，也可能减小

三、非选择题

17．如图甲所示，在

y＝0和y＝2m之间有沿着

x轴方向的匀强电场，

MN为电场区域的上边界，

在x轴方向范围足够大．电场强度的变化如图乙所示，取

x轴正方向为电场正方向，现有一个带负电

q

－2

C/kg，在t＝0时刻以速度

2

从O点沿y轴正方向进入电

的粒子，粒子的比荷为

＝×10

v0＝5×10m/s

m

场区域，不计粒子重力．求：

（1）粒子通过电场区域的时间；

（2）粒子离开电场时的位置坐标；

（3）粒子通过电场区域后沿x方向的速度大小．

18.如图甲所示，在场强大小为

E、方向竖直向上的匀强电场中存在着一半径为

R的圆形区域．

O

点为该圆形区域的圆心，A点是圆形区域的最低点，B点是圆形区域最右侧的点．在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷，电荷的质量为m、电荷量为q，不计电荷重力、电荷之间的作用力．

（1）若某电荷的运动轨迹和圆形区域的边缘交于P点．如图甲所示，∠POA＝θ，求该电荷从A点

出发时的速率；

（2）若在圆形区域的边缘有一接收屏CBD，如图乙所示，C、D分别为接收屏上最边缘的两点，∠COB

＝∠BOD＝30°.求该屏上接收到的电荷的最大动能和最小动能．

《带电粒子在匀强电场中的运动》参考答案

1、解析：

选

D.当可移动介质

P向左匀速移出的过程中，介电常数减小，电容器电容变小，选项

A

错误；电容器的电压等于电源电动势不变，电荷量

Q＝CU减小，选项

B错误；电容器放电，电流方向

M→R→N，M

点的电势比

N点的电势高，选项

C错误，D正确．

U

C

U

R1

2、解析：

选B.设油滴质量为m，电荷量为q，两板间距离为d，当其静止时，有

dq＝dq＝mg；

由题图知，增大R1，UR1增大，油滴将向上加速，增大

R2，油滴受力不变，仍保持静止；由

E＝

U知，

d

增大d，U不变时，E减小，油滴将向下加速；断开电键

S，电容器将通过R1、R2放电，两板间场强变

小，油滴将向下加速，故只有B项正确．

x

1

1

qE

2

1

qE

2

3、解析：

选

知，tP

＝

Q

y＝

·

P

P

·

Q

Q

，解

A.由OM＝MN和t＝v0

2t，在垂直极板方向上，

2

mPt

＝2

mQt

得：

mP∶mQ＝3∶4，A正确．

4、解析：

选B.粒子不能到达B板，必须做往复运动，因此粒子的运动应为：

加速→减速→反向加

速→（反向）减速．故B正确．

5、解析：

选C.

设粒子在电场中的加速度为

a.第一次，粒子恰好从下极板的边缘飞出，粒子做类平抛运动，有

L

＝v0

1

a

.第二次，设粒子飞出电场时的竖直位移为

y1，所用时间为t1

，飞出电

t，d＝at2，解得v0＝L

2d

2

场后的竖直位移为y2，所用时间为

1

2

t2，则y1＝

at1，L＝v1t1，y2＝at1·t2，L＝v1t2，y1＋y2＝d，解得v1

2

＝L

3a＝3v0，故C正确．

2d

6、解析：

选D.带正电的小球自坐标原点沿着y轴正方向以初速度v0抛出后受到恒定的合力作用

做匀变速运动，在运动开始的一段时间内合力与速度的夹角为钝角，速度减小，A、B都错；小球自坐

标原点到M点，y方向在重力作用下做速度减小到零的匀变速运动，

x方向在静电力作用下做初速度

为零的匀加速运动，所以到

M点时的动能不为零，C错；由动能定理有：

1

2

1

2

qEx＝mvN－

mv0>0，D正

2

2

确．

εrS

S不变时，增大d，

7、解析：

选A.由电容决定式

C＝

知，电容与极板间距成反比，当保持

4πkd

Q

εrS

电容减小，由电容定义式

C＝U知，板间电势差增大，静电计指针偏角

θ变大，A对，B错；由C＝4πkd，

知C与S成正比，当d不变时，减小S，C减小，Q不变，由C＝Q知U增大，θ变大，C、D均错．

U

8、解析：

选C.微粒向下偏转，则微粒受到的电场力与重力的合力向下，若微粒带正电，只要电

场力小于重力，就不能确定A、B板所带电荷的电性，A项错误；由于不能确定电场力的方向，因此不

能确定电场力做功的正负，不能确定微粒从M点运动到N点电势能的变化，B项错误；由于电场力与

重力的合力一定向下，因此微粒受到的合外力做正功，根据动能定理可知，微粒从M到N的过程中

动能增加，C项正确；由于不能确定除重力以外的力即电场力做的是正功还是负功，根据功能原理可

知，不能确定微粒从M到N过程中机械能是增加还是减少，D项错误．

9、解析：

选C.设加速电场电压为

U，偏转电压为U，极板长度为L，间距为d，电子加速过程中，

0

2

2U0q，电子进入极板后做类平抛运动，时间

t＝L，a＝Uq

由U

mv0

，得v

0＝

，v

0q＝2

m

v0

dm

y＝at，tanθ＝

vy＝UL，由此可判断

C正确．

v02U0d

10、解析：

选C.两球在竖直方向上都做自由落体运动，由于下落高度相同，所以运动时间相等，

1

A错；在水平方向上，两球都做匀加速运动，由x＝2at2可得：

aP∶aQ＝2∶1，则qP∶qQ＝2∶1，C正

确；电势能的减少量：

EPQ

PPQ

Q

P

∶ΔE

＝（qE·x）∶（q

E·x）＝4∶1，B错；动能增加量：

（mgh＋

E）∶（mgh

＋EQ）<4∶1，D错．

11、解析：

选C.由题中φ－x图，画出电场强度

所示，由图可知A错误；由牛顿第二定律知，粒子在

E随x变化的图象及带电粒子的v－t图象，如图

P、Q两点的加速度满足aP＝2aQ，B错误；由v

－t图象可知，粒子在P、Q两点对应的时间分别是

2

2

t0和（3－

2）t0，其速度相等，C正确；粒子在P、

Q两点的功率P＝Eqv，因电场强度不相同，故功率不同，

D错误．

εrS

12、解析：

选ABC.若将B极板向右平移稍许，d增大，根据C＝4πkd，知电容器的电容将减小，

故A正确．若将B极板向下平移稍许，正对面积S减小，根据C＝rS，知电容将减小，因电容器带

4πkdε

Q

电荷量Q不变，由U＝C，分析知板间电势差增大，故B正确．若将B极板向上平移稍许，正对面积

Q

U

S减小，电容将减小，因电容器带电荷量

Q不变，由U＝C，分析知板间电势差增大，根据

E＝d

，知

E增大，则小球所受的电场力增大，

θ将变大，故

C正确．轻轻将细线剪断，小球将沿重力与电场力

的合力方向做匀加速直线运动，故

D错误．

13、解析：

选BC.由速度图象可知，带电小球在区域

Ⅰ与区域Ⅱ中的加速度大小之比为

3∶2，由

mg

3

3∶5，B正确；小球在

t＝s时

牛顿第二定律可知：

F－mg＝

2，所以小球所受的重力与电场力之比为

速度为零，此时下落到最低点，由动能定理可知，重力与电场力的总功为零，故

A错误，C正确；因

小球只受重力与电场力作用，所以小球的机械能与电势能总和保持不变，

D错误．

14、解析：

选AD.不计重力的带电粒子垂直射入匀强电场中，粒子做类平抛运动且沿初速度方向

做匀速直线运动，而电场的宽度一定，故增大电场强度不会改变通过电场的时间，B项错误，D项正

确；沿场强方向做匀加速直线运动，可知粒子受力方向与场强方向一致，故粒子带正电，A项正确；

粒子位移方向与电场力方向夹角为锐角，电场力做正功，故粒子电势能减小，C项错．

15、解析：

选CD.电子在A、B板间加速

BA

12，在C、D板间的偏转位移y＝

1·Ue·L

＝UL2

，

Ue＝2mv

2md

v

4dUBA

S闭合，只向右移动滑片

P，UBA增大，偏转位移

y减小，电子打在M上的位置降低，选项

A错误；设

v

电子在A、B板间的运动时间为

t1，A、B板间距离为dAB，则dAB＝2t1，S闭合，只改变A、B板间距离，

板间电压UBA不变，v不变，t1变化，从B板射出后水平方向匀速运动速度不变，电子由

O到M经历

的时间必然变化，选项

B错误；S闭合，只改变A、B板间距离，板间电压

UBA不变，偏转位移y相同，

根据动能定理知电场力做功相同，电子到达

M瞬间的动能相同，选项

C正确；S闭合再断开，A、B

板所带电荷量不变，向左平移

B板，板间距离减小，根据C＝

εrS

Q

，C增大，U

，U

4πkdAB

BA＝C

BA减小，又

L

2

y＝1·Ue·

＝

UL

可知电子打在M上的位置升高，选项

D正确．

v

2md

4dUBA

16、解析：

选CD.

U

刚开始时粒子做匀速直线运动，mg＝qE＝qd，由受力分析可知，粒子在竖直方向上合力为零．如

U

cosθ＝q

U

U

图所示，平行金属板顺时针旋转θ角，则q

dcosθ

cosθ＝q＝mg，即竖直方向上的合

d′

d

力为0，水平方向的合力为

F＝mgtanθ，故粒子做匀加速直线运动，

A、B错C正确；由分析知电场

力做正功，粒子的电势能减小；同理，若平行金属板逆时针旋转

θ角，则粒子电势能逐渐增加，粒子

做匀减速直线运动，故选项

D正确．

17、解析：

（1）因粒子初速度方向垂直电场方向，在电场中做类平抛运动，所以粒子通过电场区域

的时间

t＝

y

－

3s.

＝4×10

v

0

Eq

1

（2）粒子沿x轴负方向先加速后减速，加速时的加速度大小为

a1＝m＝4m/s2，

E2q

减速时的加速度大小为

a2＝m＝2m/s2，

由运动学规律得x方向上的位移为

x＝

1

a1

T

＋a1

T

－

1

a2

T

－

5m

2

2

2

＝2×10

2

2

因此粒子离开电场时的位置坐标为

－

5m，2m）．

（－2×10

（3）粒子通过电场区域后沿x方向的速度为

T

T

－

3

vx＝a1

－a＝4×10

m/s.

2

2

2

－3

－5

答案：

（1）4×10s

（2）（－2×10m，2m）

－3

（3）4×10m/s

18、解析：

（1）设该电荷从A点发出时的速率为v0，运动到P点的时间为t，因不计其重力及电荷

之间的作用力，所以电荷做类平抛运动，则有

Eq

a＝m

Rsinθ＝v0t

1

R－Rcosθ＝2at2

由以上三式得

v0＝

EqRsin2θ

2m（1－cosθ）.

（2）由

（1）的结论得粒子从A点出发时的动能为

1

2

EqRsin2θ

EqR（1＋cosθ）

＝

2mv0＝4（1－cosθ）

4

则经过P点时的动能为

1

2

＝

1

E＝Eq（R－Rcosθ）＋2mv

4EqR（5－3cosθ）

k

0

可以看出，当

θ变大时，接收屏上电荷的动能逐渐增大，因此D点接收到的电荷的末动能最小，

C点接收到的电荷的末动能最大．

D点对应θ＝60°，则最小动能为：

17

EkD＝4EqR（5－3cos60°）＝8EqR

C点对应θ＝120°，则最大动能为：

113

EkC＝4EqR（5－3cos120°）＝8EqR.

答案：

见解析